本文簡要介紹 python 語言中 scipy.special.pseudo_huber 的用法。
用法:
scipy.special.pseudo_huber(delta, r, out=None) = <ufunc 'pseudo_huber'>#Pseudo-Huber損失函數。
- delta: array_like
輸入數組,指示軟二次與線性損耗變化點。
- r: array_like
輸入數組,可能表示殘差。
- out: ndarray,可選
函數結果的可選輸出數組
- res: 標量或 ndarray
計算出的Pseudo-Huber損失函數值。
參數 ::
返回 ::
注意:
與
huber一樣,pseudo_huber通常用作統計或機器學習中的穩健損失函數,以減少異常值的影響。與huber不同,pseudo_huber很平滑。通常,r表示殘差,即模型預測與數據之間的差異。那麽,對於,
pseudo_huber類似於平方誤差並且對於絕對誤差。這樣,Pseudo-Huber 損失通常可以在像平方誤差損失函數這樣的小殘差模型擬合中實現快速收斂,並且仍然減少異常值的影響()就像絕對誤差損失一樣。作為是平方誤差範圍和絕對誤差範圍之間的分界線,必須針對每個問題仔細調整。pseudo_huber也是凸的,使其適合基於梯度的優化。[1] [2]參考:
[1]Hartley、Zisserman,“計算機視覺中的多視圖幾何”。 2003。劍橋大學出版社。 p。 619
[2]沙博尼耶等人。 “計算成像中的確定性edge-preserving正則化”。 1997. IEEE 傳輸。圖像處理。 6(2):298-311。
例子:
導入所有必需的模塊。
>>> import numpy as np >>> from scipy.special import pseudo_huber, huber >>> import matplotlib.pyplot as plt計算
r=2處delta=1的函數。>>> pseudo_huber(1., 2.) 1.2360679774997898計算函數在
r=2對於不同的三角洲通過提供列表或NumPy數組三角洲.>>> pseudo_huber([1., 2., 4.], 3.) array([2.16227766, 3.21110255, 4. ])計算函數為
delta=1通過提供列表或 NumPy 數組來在多個點上r.>>> pseudo_huber(2., np.array([1., 1.5, 3., 4.])) array([0.47213595, 1. , 3.21110255, 4.94427191])通過為廣播提供兼容形狀的數組,可以針對不同的 delta 和 r 計算該函數。
>>> r = np.array([1., 2.5, 8., 10.]) >>> deltas = np.array([[1.], [5.], [9.]]) >>> print(r.shape, deltas.shape) (4,) (3, 1)>>> pseudo_huber(deltas, r) array([[ 0.41421356, 1.6925824 , 7.06225775, 9.04987562], [ 0.49509757, 2.95084972, 22.16990566, 30.90169944], [ 0.49846624, 3.06693762, 27.37435121, 40.08261642]])繪製不同 delta 的函數。
>>> x = np.linspace(-4, 4, 500) >>> deltas = [1, 2, 3] >>> linestyles = ["dashed", "dotted", "dashdot"] >>> fig, ax = plt.subplots() >>> combined_plot_parameters = list(zip(deltas, linestyles)) >>> for delta, style in combined_plot_parameters: ... ax.plot(x, pseudo_huber(delta, x), label=f"$\delta={delta}$", ... ls=style) >>> ax.legend(loc="upper center") >>> ax.set_xlabel("$x$") >>> ax.set_title("Pseudo-Huber loss function $h_{\delta}(x)$") >>> ax.set_xlim(-4, 4) >>> ax.set_ylim(0, 8) >>> plt.show()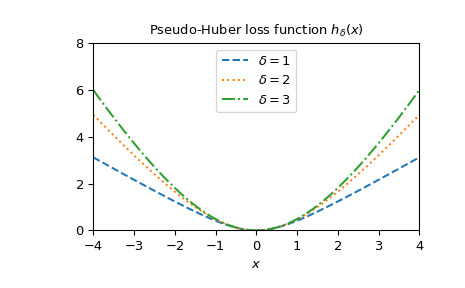
最後說明一下兩者的區別
huber和pseudo_huber通過繪製它們及其相對於的梯度r。該圖表明pseudo_huber是連續可微的,同時huber不在點上.>>> def huber_grad(delta, x): ... grad = np.copy(x) ... linear_area = np.argwhere(np.abs(x) > delta) ... grad[linear_area]=delta*np.sign(x[linear_area]) ... return grad >>> def pseudo_huber_grad(delta, x): ... return x* (1+(x/delta)**2)**(-0.5) >>> x=np.linspace(-3, 3, 500) >>> delta = 1. >>> fig, ax = plt.subplots(figsize=(7, 7)) >>> ax.plot(x, huber(delta, x), label="Huber", ls="dashed") >>> ax.plot(x, huber_grad(delta, x), label="Huber Gradient", ls="dashdot") >>> ax.plot(x, pseudo_huber(delta, x), label="Pseudo-Huber", ls="dotted") >>> ax.plot(x, pseudo_huber_grad(delta, x), label="Pseudo-Huber Gradient", ... ls="solid") >>> ax.legend(loc="upper center") >>> plt.show()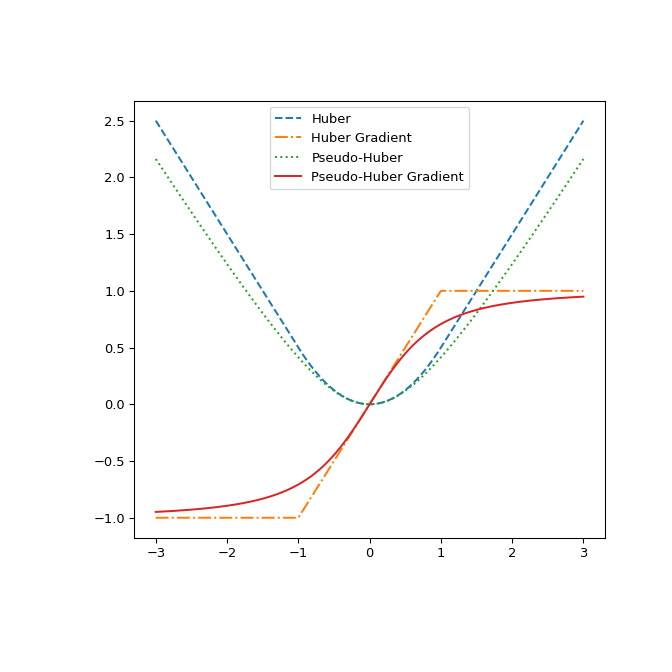
相關用法
- Python SciPy special.psi用法及代碼示例
- Python SciPy special.polygamma用法及代碼示例
- Python SciPy special.pdtr用法及代碼示例
- Python SciPy special.powm1用法及代碼示例
- Python SciPy special.poch用法及代碼示例
- Python SciPy special.perm用法及代碼示例
- Python SciPy special.exp1用法及代碼示例
- Python SciPy special.expn用法及代碼示例
- Python SciPy special.ncfdtri用法及代碼示例
- Python SciPy special.gamma用法及代碼示例
- Python SciPy special.y1用法及代碼示例
- Python SciPy special.y0用法及代碼示例
- Python SciPy special.ellip_harm_2用法及代碼示例
- Python SciPy special.i1e用法及代碼示例
- Python SciPy special.smirnovi用法及代碼示例
- Python SciPy special.ker用法及代碼示例
- Python SciPy special.ynp_zeros用法及代碼示例
- Python SciPy special.k0e用法及代碼示例
- Python SciPy special.j1用法及代碼示例
- Python SciPy special.logsumexp用法及代碼示例
- Python SciPy special.expit用法及代碼示例
- Python SciPy special.nbdtrik用法及代碼示例
- Python SciPy special.nbdtrin用法及代碼示例
- Python SciPy special.seterr用法及代碼示例
- Python SciPy special.ncfdtr用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.special.pseudo_huber。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
