Python SciPy optimize.curve_fit用法及代碼示例

本文簡要介紹 python 語言中 scipy.optimize.curve_fit 的用法。

用法:

scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=None, bounds=(-inf, inf), method=None, jac=None, *, full_output=False, nan_policy=None, **kwargs)#

使用非線性最小二乘法將函數 f 擬合到數據。

假設 ydata = f(xdata, *params) + eps 。

參數 ：：

f： 可調用的

模型函數 f(x, …)。它必須將自變量作為第一個參數，並將要擬合的參數作為單獨的剩餘參數。

xdata： array_like

測量數據的自變量。對於具有 k 個預測變量的函數，通常應該是 M-length 序列或 (k,M) 形數組，並且如果每個元素是類似數組的對象，則每個元素都應該是 float 可轉換的。

ydata： array_like

依賴數據，一個長度為 M 的數組 - 名義上是 f(xdata, ...) 。

p0： 數組，可選

參數的初始猜測(長度 N)。如果為 None，則初始值全部為 1(如果可以使用內省確定函數的參數數量，否則會引發 ValueError)。

sigma： 無或標量或M-length序列或MxM數組，可選

確定不確定性數據.如果我們將殘差定義為r = ydata - f(xdata, *popt), 那麽解釋西格瑪取決於它的維數：

• A scalar or 1-D sigma should contain values of standard deviations of errors in ydata. In this case, the optimized function is chisq = sum((r / sigma) ** 2).

• A 2-D sigma should contain the covariance matrix of errors in ydata. In this case, the optimized function is chisq = r.T @ inv(sigma) @ r.

無(默認)等效於用 1 填充的一維 sigma。

absolute_sigma： 布爾型，可選

如果為 True，則以絕對意義使用 sigma，估計的參數協方差 pcov 反映了這些絕對值。

如果為 False(默認)，則隻有西格瑪值很重要。返回的參數協方差矩陣pcov基於縮放西格瑪由一個常數因子。這個常數是通過要求減少的奇斯克為最優參數流行音樂使用時縮放 西格瑪等於統一。換一種說法，西格瑪被縮放以匹配擬合後殘差的樣本方差。默認為假。數學上，pcov(absolute_sigma=False) = pcov(absolute_sigma=True) * chisq(popt)/(M-N)

check_finite： 布爾型，可選

如果為 True，則檢查輸入數組是否不包含 infs 的 nan，如果包含，則引發 ValueError。如果輸入數組確實包含 nan，則將此參數設置為 False 可能會默默地產生無意義的結果。如果未明確指定nan_policy，則默認值為 True，否則為 False。

bounds： 數組 或 Bounds 的 2 元組，可選

參數的下限和上限。默認為無限製。有兩種方法可以指定邊界：

• Instance of Bounds class.

• 2-tuple of array_like: Each element of the tuple must be either an array with the length equal to the number of parameters, or a scalar (in which case the bound is taken to be the same for all parameters). Use np.inf with an appropriate sign to disable bounds on all or some parameters.

method： {‘lm’, ‘trf’, ‘dogbox’}，可選

用於優化的方法。看scipy.optimize.least_squares更多細節。對於無約束問題，默認值為 ‘lm’，如果為 ‘trf’界限提供。當觀測值數量小於變量數量時，‘lm’ 方法將不起作用，在這種情況下使用‘trf’ 或‘dogbox’。

jac： 可調用，字符串或無，可選

帶簽名的函數jac(x, ...)它將模型函數關於參數的雅可比矩陣計算為密集的類數組結構。它將根據提供的縮放西格瑪。如果無(默認)，將以數字方式估計雅可比行列式。 ‘trf’ 和 ‘dogbox’ 方法的字符串關鍵字可用於選擇有限差分方案，請參閱scipy.optimize.least_squares.

full_output： 布爾值，可選

如果為 True，此函數返回附加信息：infodict、mesg 和 ier。

nan_policy： {‘raise’, ‘omit’，無}，可選

定義當輸入包含 nan 時如何處理。可以使用以下選項(默認為“無”)：

• ‘raise’: throws an error

• ‘omit’: performs the calculations ignoring nan values

• None: no special handling of NaNs is performed (except what is done by check_finite); the behavior when NaNs are present is implementation-dependent and may change.

請注意，如果顯式指定該值(而不是“無”)，check_finite將被設置為 False。

**kwargs：

關鍵字參數傳遞給 leastsq 用於 method='lm' 或 least_squares 否則。

返回 ：：

popt： 數組

參數的最佳值，使f(xdata, *popt) - ydata 的殘差平方和最小化。

pcov： 二維陣列

popt 的估計近似協方差。對角線提供參數估計的方差。要計算參數的一個標準差誤差，請使用perr = np.sqrt(np.diag(pcov))。注意之間的關係冠狀病毒參數誤差估計是基於模型函數圍繞最優值的線性近似得出的[1]。當這種近似變得不準確時，冠狀病毒可能無法提供準確的不確定性測量。

如上所述，sigma 參數如何影響估計的協方差取決於 absolute_sigma 參數。

如果解中的雅可比矩陣沒有滿秩，則 ‘lm’ 方法返回一個用 np.inf 填充的矩陣，另一方麵 ‘trf’ 和 ‘dogbox’ 方法使用 Moore-Penrose 偽逆來計算協方差矩陣。具有較大條件數的協方差矩陣(例如使用 numpy.linalg.cond 計算)可能表明結果不可靠。

infodict： dict(僅在full_output是真的)

帶有鍵的可選輸出字典：

nfev

函數調用的次數。與‘lm’ 方法相反，方法‘trf’ 和‘dogbox’ 不計算數值雅可比近似值的函數調用。

fvec

對於一維，在解中評估的殘差值西格瑪這是(f(x, *popt) - ydata)/sigma.

fjac

最終近似雅可比矩陣的 QR 分解的 R 矩陣的排列，按列存儲。與 ipvt 一起，可以近似估計估計的協方差。方法‘lm’ 僅提供此信息。

ipvt

一個長度為 N 的整數數組，它定義了一個置換矩陣 p，使得 fjac*p = q*r，其中 r 是具有非遞增大小的對角線元素的上三角形。 p 的 j 列是單位矩陣的 ipvt(j) 列。方法‘lm’ 僅提供此信息。

qtf

向量 (transpose(q) * fvec)。方法‘lm’ 僅提供此信息。

mesg： str (僅在full_output是真的)

提供有關解決方案信息的字符串消息。

ier： int(僅在以下情況下返回full_output是真的)

一個整數標誌。如果它等於 1、2、3 或 4，則找到了解決方案。否則，找不到解決方案。在任何一種情況下，可選的輸出變量 mesg 都會提供更多信息。

拋出 ：：

ValueError

如果 ydata 或 xdata 包含 NaN，或者使用了不兼容的選項。

RuntimeError

如果最小二乘最小化失敗。

OptimizeWarning

如果無法估計參數的協方差。

注意：

用戶應確保輸入擴展數據,數據，以及輸出f是float64，否則優化可能會返回不正確的結果。

對於 method='lm' ，該算法通過 leastsq 使用 Levenberg-Marquardt 算法。請注意，該算法隻能處理無約束問題。

框約束可以通過方法‘trf’和‘dogbox’處理。有關更多信息，請參閱 least_squares 的文檔字符串。

參考：

[1] K.Vugrin 等人。非線性置信區域估計技術：

地下水流回歸：三個案例研究。水資源研究，卷。 43、W03423、DOI:10.1029/2005WR004804

例子：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.optimize import curve_fit

>>> def func(x, a, b, c):
...     return a * np.exp(-b * x) + c

定義要適應一些噪聲的數據：

>>> xdata = np.linspace(0, 4, 50)
>>> y = func(xdata, 2.5, 1.3, 0.5)
>>> rng = np.random.default_rng()
>>> y_noise = 0.2 * rng.normal(size=xdata.size)
>>> ydata = y + y_noise
>>> plt.plot(xdata, ydata, 'b-', label='data')

擬合函數 func 的參數 a、b、c：

>>> popt, pcov = curve_fit(func, xdata, ydata)
>>> popt
array([2.56274217, 1.37268521, 0.47427475])
>>> plt.plot(xdata, func(xdata, *popt), 'r-',
...          label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

將優化限製在 0 <= a <= 3 、 0 <= b <= 1 和 0 <= c <= 0.5 的區域：

>>> popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
>>> popt
array([2.43736712, 1.        , 0.34463856])
>>> plt.plot(xdata, func(xdata, *popt), 'g--',
...          label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.legend()
>>> plt.show()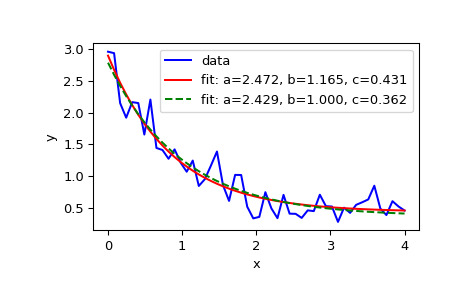

為了獲得可靠的結果，模型函數不應過度參數化；冗餘參數可能導致協方差矩陣不可靠，並且在某些情況下，擬合質量較差。為了快速檢查模型是否可能過度參數化，請計算協方差矩陣的條件數：

>>> np.linalg.cond(pcov)
34.571092161547405  # may vary

該值很小，因此不會引起太大關注。但是，如果我們要添加第四個參數d到函數效果與a：

>>> def func(x, a, b, c, d):
...     return a * d * np.exp(-b * x) + c  # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
>>> np.linalg.cond(pcov)
1.13250718925596e+32  # may vary

如此大的數值令人擔憂。協方差矩陣的對角線元素與擬合的不確定性相關，提供了更多信息：

>>> np.diag(pcov)
array([1.48814742e+29, 3.78596560e-02, 5.39253738e-03, 2.76417220e+28])  # may vary

請注意，第一項和最後一項比其他元素大得多，這表明這些參數的最佳值不明確，並且模型中隻需要其中一個參數。