本文簡要介紹 python 語言中 scipy.optimize.root 的用法。
用法:
scipy.optimize.root(fun, x0, args=(), method='hybr', jac=None, tol=None, callback=None, options=None)#求向量函數的根。
- fun: 可調用的
求根的向量函數。
- x0: ndarray
初步猜測。
- args: 元組,可選
傳遞給目標函數及其雅可比行列式的額外參數。
- method: str,可選
求解器的類型。應該是其中之一
‘hybr’ (see here)
‘lm’ (see here)
‘broyden1’ (see here)
‘broyden2’ (see here)
‘anderson’ (see here)
‘linearmixing’ (see here)
‘diagbroyden’ (see here)
‘excitingmixing’ (see here)
‘krylov’ (see here)
‘df-sane’ (see here)
- jac: 布爾或可調用,可選
如果 jac 是一個布爾值並且為 True,則 fun 假定返回 Jacobian 的值以及目標函數。如果為 False,Jacobian 將以數值方式估計。 jac 也可以是一個可調用的返回有趣的雅可比行列式。在這種情況下,它必須接受與 fun 相同的參數。
- tol: 浮點數,可選
容忍終止。如需詳細控製,請使用solver-specific 選項。
- callback: 函數,可選
可選的回調函數。它在每次迭代中被調用為
callback(x, f)其中x是當前的解決方案,並且f相應的殘差。適用於除 ‘hybr’ 和 ‘lm’ 之外的所有方法。- options: 字典,可選
求解器選項字典。例如:,xtol或者馬克西特, 看scipy.optimize.show_options詳情。
- sol: OptimizeResult
解決方案表示為
OptimizeResult對象。重要屬性是:x解決方案數組,success指示算法是否成功退出的布爾標誌和說明終止原因的message。有關其他屬性的說明,請參見OptimizeResult。
參數 ::
返回 ::
注意:
本節介紹可通過 ‘method’ 參數選擇的可用求解器。默認方法是 hybr。
方法混合動力使用 MINPACK 中實現的 Powell 混合方法的修改[1].
方法流明使用在MINPACK 中實現的Levenberg-Marquardt 算法的修改,以最小二乘的方式求解非線性方程組[1].
方法df-sane是derivative-free頻譜法。[3]
方法布羅伊登1,布羅伊登2,安德森,線性混合,迪亞布羅伊登,令人興奮的混合,克雷洛夫是不精確的牛頓方法,具有回溯或全行搜索[2].每種方法對應於特定的雅可比近似。
方法 broyden1 使用 Broyden 的第一個 Jacobian 近似,被稱為 Broyden 的好方法。
方法 broyden2 使用 Broyden 的第二雅可比近似,它被稱為 Broyden 壞方法。
方法安德森使用(擴展)安德森混合。
方法 Krylov 將 Krylov 近似用於逆雅可比行列式。它適用於large-scale 問題。
方法 diagbroyden 使用對角線 Broyden Jacobian 近似。
方法線性混合使用標量雅可比近似。
方法激發混合使用調諧對角雅可比近似。
警告
為方法diagbroyden、linearmixing和excitingmixing實現的算法可能對特定問題有用,但它們是否有效可能很大程度上取決於問題。
參考:
[1] (1,2)更多,Jorge J.、Burton S. Garbow 和 Kenneth E. Hillstrom。 1980. MINPACK-1 用戶指南。
[2]C. T. 凱利。 1995. 線性和非線性方程的迭代方法。工業和應用數學學會。 <https://archive.siam.org/books/kelley/fr16/>
[3]拉克魯茲,J.M.馬丁內斯,M.雷丹。數學。比較。 75, 1429 (2006)。
例子:
以下函數定義非線性方程組及其雅可比。
>>> import numpy as np >>> def fun(x): ... return [x[0] + 0.5 * (x[0] - x[1])**3 - 1.0, ... 0.5 * (x[1] - x[0])**3 + x[1]]>>> def jac(x): ... return np.array([[1 + 1.5 * (x[0] - x[1])**2, ... -1.5 * (x[0] - x[1])**2], ... [-1.5 * (x[1] - x[0])**2, ... 1 + 1.5 * (x[1] - x[0])**2]])可以如下獲得解決方案。
>>> from scipy import optimize >>> sol = optimize.root(fun, [0, 0], jac=jac, method='hybr') >>> sol.x array([ 0.8411639, 0.1588361])大問題
假設我們需要在正方形 上求解以下積分微分方程:
和 在廣場邊界的其他地方。
可以使用
method='krylov'求解器找到解決方案:>>> from scipy import optimize >>> # parameters >>> nx, ny = 75, 75 >>> hx, hy = 1./(nx-1), 1./(ny-1)>>> P_left, P_right = 0, 0 >>> P_top, P_bottom = 1, 0>>> def residual(P): ... d2x = np.zeros_like(P) ... d2y = np.zeros_like(P) ... ... d2x[1:-1] = (P[2:] - 2*P[1:-1] + P[:-2]) / hx/hx ... d2x[0] = (P[1] - 2*P[0] + P_left)/hx/hx ... d2x[-1] = (P_right - 2*P[-1] + P[-2])/hx/hx ... ... d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy ... d2y[:,0] = (P[:,1] - 2*P[:,0] + P_bottom)/hy/hy ... d2y[:,-1] = (P_top - 2*P[:,-1] + P[:,-2])/hy/hy ... ... return d2x + d2y - 10*np.cosh(P).mean()**2>>> guess = np.zeros((nx, ny), float) >>> sol = optimize.root(residual, guess, method='krylov') >>> print('Residual: %g' % abs(residual(sol.x)).max()) Residual: 5.7972e-06 # may vary>>> import matplotlib.pyplot as plt >>> x, y = np.mgrid[0:1:(nx*1j), 0:1:(ny*1j)] >>> plt.pcolormesh(x, y, sol.x, shading='gouraud') >>> plt.colorbar() >>> plt.show()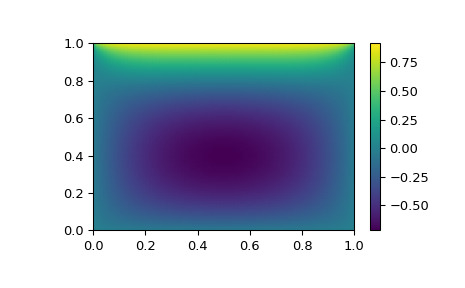
相關用法
- Python SciPy optimize.root_scalar用法及代碼示例
- Python SciPy optimize.rosen_der用法及代碼示例
- Python SciPy optimize.rosen用法及代碼示例
- Python SciPy optimize.rosen_hess用法及代碼示例
- Python SciPy optimize.rosen_hess_prod用法及代碼示例
- Python SciPy optimize.ridder用法及代碼示例
- Python SciPy optimize.line_search用法及代碼示例
- Python SciPy optimize.shgo用法及代碼示例
- Python SciPy optimize.minimize_scalar用法及代碼示例
- Python SciPy optimize.fmin用法及代碼示例
- Python SciPy optimize.NonlinearConstraint用法及代碼示例
- Python SciPy optimize.KrylovJacobian用法及代碼示例
- Python SciPy optimize.toms748用法及代碼示例
- Python SciPy optimize.linprog_verbose_callback用法及代碼示例
- Python SciPy optimize.bracket用法及代碼示例
- Python SciPy optimize.milp用法及代碼示例
- Python SciPy optimize.diagbroyden用法及代碼示例
- Python SciPy optimize.bisect用法及代碼示例
- Python SciPy optimize.isotonic_regression用法及代碼示例
- Python SciPy optimize.golden用法及代碼示例
- Python SciPy optimize.brute用法及代碼示例
- Python SciPy optimize.newton用法及代碼示例
- Python SciPy optimize.fsolve用法及代碼示例
- Python SciPy optimize.Bounds用法及代碼示例
- Python SciPy optimize.fixed_point用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.optimize.root。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
