Python SciPy sampling.DiscreteAliasUrn用法及代码示例

本文简要介绍 python 语言中 scipy.stats.sampling.DiscreteAliasUrn 的用法。

用法:

class  scipy.stats.sampling.DiscreteAliasUrn(dist, *, domain=None, urn_factor=1, random_state=None)#

离散Alias-Urn 方法。

该方法用于从具有有限域的单变量离散分布中采样。它使用大小为\(N\) 的概率向量或具有有限支持的概率质量函数从分布中生成随机数。

参数 ：：

dist： 数组 或对象，可选

分布的概率向量 (PV)。如果 PV 不可用，则需要一个具有 pmf 方法的类的实例。 PMF 的签名预计为：def pmf(self, k: int) -> float。即它应该接受一个 Python 整数并返回一个 Python 浮点数。

domain： 整数，可选

支持 PMF。如果概率向量 (pv) 不可用，则必须给出有限域。即 PMF 必须有一个有限的支持。默认为 None 。当 None ：

• 如果一个support方法由分发对象提供距离，用于设置分布的域。

• 否则，假定支持为 (0, len(pv)) 。当此参数与概率向量一起传递时，domain[0] 用于将分布从 (0, len(pv)) 重新定位到 (domain[0], domain[0]+len(pv))，而 domain[1] 将被忽略。有关更详细的说明，请参阅注释和教程。

urn_factor： 浮点数，可选

瓮表的大小相对于概率向量的大小。它不能小于 1。更大的表会导致更快的生成时间，但需要更昂贵的设置。默认值为 1。

random_state： {无，整数， numpy.random.Generator ，

numpy.random.RandomState}, optional

NumPy 随机数生成器或底层NumPy 随机数生成器的种子，用于生成统一随机数流。如果random_state是无(或np.random)， 这numpy.random.RandomState使用单例。如果random_state是一个 int，一个新的RandomState使用实例，播种random_state.如果random_state已经是一个Generator或者RandomState实例然后使用该实例。

注意：

当有限概率向量可用或分布的 PMF 可用时，此方法有效。如果只有 PMF 可用，则还必须给出 PMF 的有限支持(域)。建议首先通过评估支持中每个点的 PMF 来获得概率向量，然后再使用它。

如果给定一个概率向量，它必须是一个非负浮点数的一维数组，没有任何 inf 或 nan 值。此外，必须至少有一个非零条目，否则会引发异常。

默认情况下，概率向量从 0 开始索引。但是，这可以通过传递 domain 参数来更改。当 domain 与 PV 一起给出时，它具有将分布从 (0, len(pv)) 重新定位到 (domain[0] 、 domain[0] + len(pv)) 的效果。 domain[1] 在这种情况下被忽略。

可以增加参数urn_factor 以加快生成速度，但会增加设置时间。此方法使用表来生成随机变量。 urn_factor 控制此表相对于概率向量的大小(或支持的宽度，以防 PV 不可用)的大小。由于此表是在设置期间计算的，因此增加此参数会线性增加设置所需的时间。建议将此参数保持在 2 以下。

参考：

[1]

UNU.RAN 参考手册，第 5.8.2 节，“DAU -(离散)Alias-Urn 方法”，http://statmath.wu.ac.at/software/unuran/doc/unuran.html#DAU

[2]

A.J.沃克 (1977)。一种生成具有一般分布的离散随机变量的有效方法，ACM Trans。数学。软件 3，第 253-256 页。

例子：

>>> from scipy.stats.sampling import DiscreteAliasUrn
>>> import numpy as np

要使用概率向量创建随机数生成器，请使用：

>>> pv = [0.1, 0.3, 0.6]
>>> urng = np.random.default_rng()
>>> rng = DiscreteAliasUrn(pv, random_state=urng)

RNG 已设置完毕。现在，我们现在可以使用 rvs 方法从分布中生成样本：

>>> rvs = rng.rvs(size=1000)

为了验证随机变量是否遵循给定分布，我们可以使用卡方检验(作为goodness-of-fit 的度量)：

>>> from scipy.stats import chisquare
>>> _, freqs = np.unique(rvs, return_counts=True)
>>> freqs = freqs / np.sum(freqs)
>>> freqs
array([0.092, 0.292, 0.616])
>>> chisquare(freqs, pv).pvalue
0.9993602047563164

由于 p 值非常高，我们无法拒绝观察到的频率与预期频率相同的零假设。因此，我们可以安全地假设变量是根据给定的分布生成的。请注意，这只是给出了算法的正确性，而不是样本的质量。

如果 PV 不可用，也可以传递具有 PMF 方法和有限域的类的实例。

>>> urng = np.random.default_rng()
>>> class Binomial:
...     def __init__(self, n, p):
...         self.n = n
...         self.p = p
...     def pmf(self, x):
...         # note that the pmf doesn't need to be normalized.
...         return self.p**x * (1-self.p)**(self.n-x)
...     def support(self):
...         return (0, self.n)
...
>>> n, p = 10, 0.2
>>> dist = Binomial(n, p)
>>> rng = DiscreteAliasUrn(dist, random_state=urng)

现在，我们可以使用 rvs 方法从分布中采样，并测量样本的 goodness-of-fit：

>>> rvs = rng.rvs(1000)
>>> _, freqs = np.unique(rvs, return_counts=True)
>>> freqs = freqs / np.sum(freqs)
>>> obs_freqs = np.zeros(11)  # some frequencies may be zero.
>>> obs_freqs[:freqs.size] = freqs
>>> pv = [dist.pmf(i) for i in range(0, 11)]
>>> pv = np.asarray(pv) / np.sum(pv)
>>> chisquare(obs_freqs, pv).pvalue
0.9999999999999999

为了检查样本是否来自正确的分布，我们可以可视化样本的直方图：

>>> import matplotlib.pyplot as plt
>>> rvs = rng.rvs(1000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> x = np.arange(0, n+1)
>>> fx = dist.pmf(x)
>>> fx = fx / fx.sum()
>>> ax.plot(x, fx, 'bo', label='true distribution')
>>> ax.vlines(x, 0, fx, lw=2)
>>> ax.hist(rvs, bins=np.r_[x, n+1]-0.5, density=True, alpha=0.5,
...         color='r', label='samples')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PMF(x)')
>>> ax.set_title('Discrete Alias Urn Samples')
>>> plt.legend()
>>> plt.show()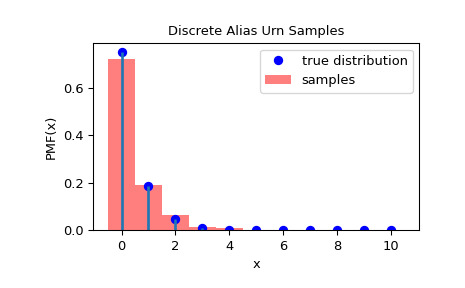

要设置 urn_factor ，请使用：

>>> rng = DiscreteAliasUrn(pv, urn_factor=2, random_state=urng)

这使用两倍于概率向量大小的表格从分布中生成随机变量。