本文简要介绍 python 语言中 scipy.signal.welch 的用法。
用法:
scipy.signal.welch(x, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, average='mean')#使用 Welch 方法估计功率谱密度。
Welch 的方法 [1] 通过将数据划分为重叠段、为每个段计算修改的周期图并对周期图进行平均来计算功率谱密度的估计值。
- x: array_like
测量值的时间序列
- fs: 浮点数,可选
x 时间序列的采样频率。默认为 1.0。
- window: str 或 tuple 或 数组,可选
想要使用的窗口。如果窗户是一个字符串或元组,它被传递给scipy.signal.get_window生成窗口值,默认为DFT-even。看scipy.signal.get_window获取窗口列表和所需参数。如果窗户是数组,它将直接用作窗口,其长度必须为nperseg。默认为 Hann 窗口。
- nperseg: 整数,可选
每个段的长度。默认为 None,但如果 window 是 str 或 tuple,则设置为 256,如果 window 是 数组,则设置为窗口的长度。
- noverlap: 整数,可选
段之间重叠的点数。如果None,
noverlap = nperseg // 2.默认为None.- nfft: 整数,可选
如果需要零填充 FFT,则使用的 FFT 的长度。如果没有,FFT 长度为 nperseg。默认为无。
- detrend: str 或函数 或False, 可选的
指定如何去除每个段的趋势。如果scipy.signal.detrend是一个字符串,它作为类型参数scipy.signal.detrend函数。如果它是一个函数,它接受一个段并返回一个去趋势的段。如果scipy.signal.detrend是False,没有去趋势。默认为‘constant’。
- return_onesided: 布尔型,可选
如果为 True,则返回真实数据的单侧频谱。如果为 False,则返回两侧频谱。默认为 True,但对于复杂数据,始终返回两侧频谱。
- scaling: { ‘density’, ‘spectrum’ },可选
在计算 Pxx 的单位为 V**2/Hz 的功率谱密度 (‘density’) 和计算 Pxx 的单位为 V**2 的功率谱 (‘spectrum’) 之间进行选择,如果 x 以 V 为单位测量并且fs 以赫兹为单位。默认为‘density’
- axis: 整数,可选
计算周期图的轴;默认值在最后一个轴上(即
axis=-1)。- average: { ‘mean’, ‘median’ },可选
平均周期图时使用的方法。默认为‘mean’。
- f: ndarray
采样频率数组。
- Pxx: ndarray
x 的功率谱密度或功率谱。
参数 ::
返回 ::
注意:
适当的重叠量取决于窗口的选择和您的要求。对于默认的 Hann 窗口,50% 的重叠是在准确估计信号功率和不过度计算任何数据之间的合理权衡。较窄的窗口可能需要较大的重叠。
如果重叠为 0,此方法等价于 Bartlett 方法[2].
参考:
[1]P. Welch,“使用快速傅里叶变换来估计功率谱:一种基于对短的修改周期图进行时间平均的方法”,IEEE Trans。音频电声。卷。 15,第 70-73 页,1967 年。
[2]小姐。 Bartlett,“周期图分析和连续频谱”,Biometrika,第一卷。 37,第 1-16 页,1950 年。
例子:
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()生成一个测试信号,一个 1234 Hz 的 2 Vrms 正弦波,被 10 kHz 采样的 0.001 V**2/Hz 白噪声破坏。
>>> fs = 10e3 >>> N = 1e5 >>> amp = 2*np.sqrt(2) >>> freq = 1234.0 >>> noise_power = 0.001 * fs / 2 >>> time = np.arange(N) / fs >>> x = amp*np.sin(2*np.pi*freq*time) >>> x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)计算并绘制功率谱密度。
>>> f, Pxx_den = signal.welch(x, fs, nperseg=1024) >>> plt.semilogy(f, Pxx_den) >>> plt.ylim([0.5e-3, 1]) >>> plt.xlabel('frequency [Hz]') >>> plt.ylabel('PSD [V**2/Hz]') >>> plt.show()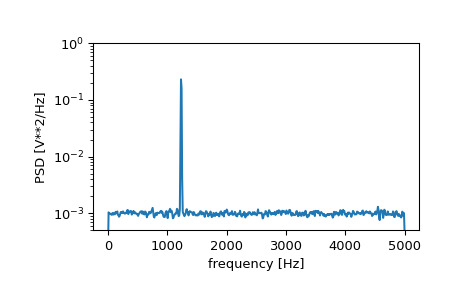
如果我们平均频谱密度的后半部分,以排除峰值,我们可以恢复信号上的噪声功率。
>>> np.mean(Pxx_den[256:]) 0.0009924865443739191现在计算并绘制功率谱。
>>> f, Pxx_spec = signal.welch(x, fs, 'flattop', 1024, scaling='spectrum') >>> plt.figure() >>> plt.semilogy(f, np.sqrt(Pxx_spec)) >>> plt.xlabel('frequency [Hz]') >>> plt.ylabel('Linear spectrum [V RMS]') >>> plt.show()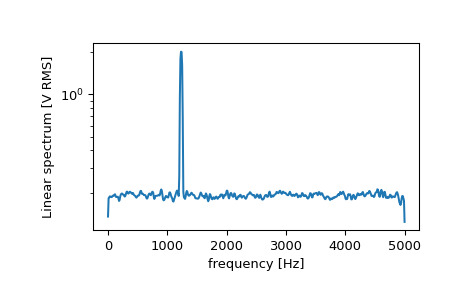
功率谱中的峰值高度是 RMS 幅度的估计值。
>>> np.sqrt(Pxx_spec.max()) 2.0077340678640727如果我们现在在信号中引入不连续性,通过将一小部分信号的幅度增加 50,我们可以看到平均功率谱密度的损坏,但使用中值平均值可以更好地估计正常行为。
>>> x[int(N//2):int(N//2)+10] *= 50. >>> f, Pxx_den = signal.welch(x, fs, nperseg=1024) >>> f_med, Pxx_den_med = signal.welch(x, fs, nperseg=1024, average='median') >>> plt.semilogy(f, Pxx_den, label='mean') >>> plt.semilogy(f_med, Pxx_den_med, label='median') >>> plt.ylim([0.5e-3, 1]) >>> plt.xlabel('frequency [Hz]') >>> plt.ylabel('PSD [V**2/Hz]') >>> plt.legend() >>> plt.show()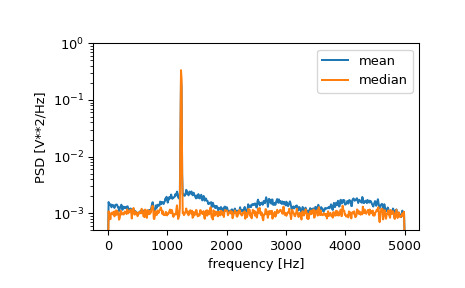
相关用法
- Python SciPy signal.wiener用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
- Python SciPy signal.kaiser_atten用法及代码示例
- Python SciPy signal.oaconvolve用法及代码示例
- Python SciPy signal.hilbert用法及代码示例
- Python SciPy signal.ricker用法及代码示例
- Python SciPy signal.group_delay用法及代码示例
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.get_window用法及代码示例
- Python SciPy signal.lfilter用法及代码示例
- Python SciPy signal.morlet用法及代码示例
- Python SciPy signal.coherence用法及代码示例
- Python SciPy signal.dfreqresp用法及代码示例
- Python SciPy signal.TransferFunction用法及代码示例
- Python SciPy signal.dbode用法及代码示例
- Python SciPy signal.residuez用法及代码示例
- Python SciPy signal.bilinear_zpk用法及代码示例
- Python SciPy signal.firls用法及代码示例
- Python SciPy signal.impulse用法及代码示例
- Python SciPy signal.buttord用法及代码示例
- Python SciPy signal.find_peaks用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.welch。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
