本文簡要介紹 python 語言中 scipy.signal.welch 的用法。
用法:
scipy.signal.welch(x, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, average='mean')#使用 Welch 方法估計功率譜密度。
Welch 的方法 [1] 通過將數據劃分為重疊段、為每個段計算修改的周期圖並對周期圖進行平均來計算功率譜密度的估計值。
- x: array_like
測量值的時間序列
- fs: 浮點數,可選
x 時間序列的采樣頻率。默認為 1.0。
- window: str 或 tuple 或 數組,可選
想要使用的窗口。如果窗戶是一個字符串或元組,它被傳遞給scipy.signal.get_window生成窗口值,默認為DFT-even。看scipy.signal.get_window獲取窗口列表和所需參數。如果窗戶是數組,它將直接用作窗口,其長度必須為nperseg。默認為 Hann 窗口。
- nperseg: 整數,可選
每個段的長度。默認為 None,但如果 window 是 str 或 tuple,則設置為 256,如果 window 是 數組,則設置為窗口的長度。
- noverlap: 整數,可選
段之間重疊的點數。如果None,
noverlap = nperseg // 2.默認為None.- nfft: 整數,可選
如果需要零填充 FFT,則使用的 FFT 的長度。如果沒有,FFT 長度為 nperseg。默認為無。
- detrend: str 或函數 或False, 可選的
指定如何去除每個段的趨勢。如果scipy.signal.detrend是一個字符串,它作為類型參數scipy.signal.detrend函數。如果它是一個函數,它接受一個段並返回一個去趨勢的段。如果scipy.signal.detrend是False,沒有去趨勢。默認為‘constant’。
- return_onesided: 布爾型,可選
如果為 True,則返回真實數據的單側頻譜。如果為 False,則返回兩側頻譜。默認為 True,但對於複雜數據,始終返回兩側頻譜。
- scaling: { ‘density’, ‘spectrum’ },可選
在計算 Pxx 的單位為 V**2/Hz 的功率譜密度 (‘density’) 和計算 Pxx 的單位為 V**2 的功率譜 (‘spectrum’) 之間進行選擇,如果 x 以 V 為單位測量並且fs 以赫茲為單位。默認為‘density’
- axis: 整數,可選
計算周期圖的軸;默認值在最後一個軸上(即
axis=-1)。- average: { ‘mean’, ‘median’ },可選
平均周期圖時使用的方法。默認為‘mean’。
- f: ndarray
采樣頻率數組。
- Pxx: ndarray
x 的功率譜密度或功率譜。
參數 ::
返回 ::
注意:
適當的重疊量取決於窗口的選擇和您的要求。對於默認的 Hann 窗口,50% 的重疊是在準確估計信號功率和不過度計算任何數據之間的合理權衡。較窄的窗口可能需要較大的重疊。
如果重疊為 0,此方法等價於 Bartlett 方法[2].
參考:
[1]P. Welch,“使用快速傅裏葉變換來估計功率譜:一種基於對短的修改周期圖進行時間平均的方法”,IEEE Trans。音頻電聲。卷。 15,第 70-73 頁,1967 年。
[2]小姐。 Bartlett,“周期圖分析和連續頻譜”,Biometrika,第一卷。 37,第 1-16 頁,1950 年。
例子:
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()生成一個測試信號,一個 1234 Hz 的 2 Vrms 正弦波,被 10 kHz 采樣的 0.001 V**2/Hz 白噪聲破壞。
>>> fs = 10e3 >>> N = 1e5 >>> amp = 2*np.sqrt(2) >>> freq = 1234.0 >>> noise_power = 0.001 * fs / 2 >>> time = np.arange(N) / fs >>> x = amp*np.sin(2*np.pi*freq*time) >>> x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)計算並繪製功率譜密度。
>>> f, Pxx_den = signal.welch(x, fs, nperseg=1024) >>> plt.semilogy(f, Pxx_den) >>> plt.ylim([0.5e-3, 1]) >>> plt.xlabel('frequency [Hz]') >>> plt.ylabel('PSD [V**2/Hz]') >>> plt.show()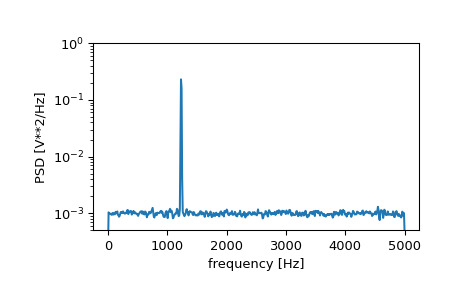
如果我們平均頻譜密度的後半部分,以排除峰值,我們可以恢複信號上的噪聲功率。
>>> np.mean(Pxx_den[256:]) 0.0009924865443739191現在計算並繪製功率譜。
>>> f, Pxx_spec = signal.welch(x, fs, 'flattop', 1024, scaling='spectrum') >>> plt.figure() >>> plt.semilogy(f, np.sqrt(Pxx_spec)) >>> plt.xlabel('frequency [Hz]') >>> plt.ylabel('Linear spectrum [V RMS]') >>> plt.show()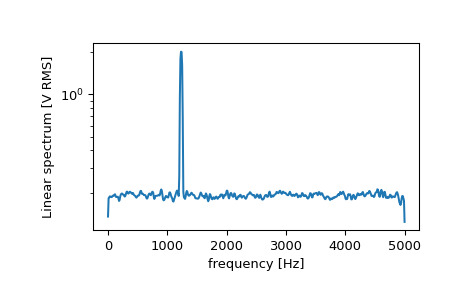
功率譜中的峰值高度是 RMS 幅度的估計值。
>>> np.sqrt(Pxx_spec.max()) 2.0077340678640727如果我們現在在信號中引入不連續性,通過將一小部分信號的幅度增加 50,我們可以看到平均功率譜密度的損壞,但使用中值平均值可以更好地估計正常行為。
>>> x[int(N//2):int(N//2)+10] *= 50. >>> f, Pxx_den = signal.welch(x, fs, nperseg=1024) >>> f_med, Pxx_den_med = signal.welch(x, fs, nperseg=1024, average='median') >>> plt.semilogy(f, Pxx_den, label='mean') >>> plt.semilogy(f_med, Pxx_den_med, label='median') >>> plt.ylim([0.5e-3, 1]) >>> plt.xlabel('frequency [Hz]') >>> plt.ylabel('PSD [V**2/Hz]') >>> plt.legend() >>> plt.show()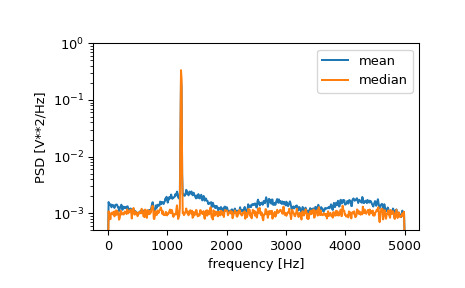
相關用法
- Python SciPy signal.wiener用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
- Python SciPy signal.kaiser_atten用法及代碼示例
- Python SciPy signal.oaconvolve用法及代碼示例
- Python SciPy signal.hilbert用法及代碼示例
- Python SciPy signal.ricker用法及代碼示例
- Python SciPy signal.group_delay用法及代碼示例
- Python SciPy signal.cheb2ord用法及代碼示例
- Python SciPy signal.get_window用法及代碼示例
- Python SciPy signal.lfilter用法及代碼示例
- Python SciPy signal.morlet用法及代碼示例
- Python SciPy signal.coherence用法及代碼示例
- Python SciPy signal.dfreqresp用法及代碼示例
- Python SciPy signal.TransferFunction用法及代碼示例
- Python SciPy signal.dbode用法及代碼示例
- Python SciPy signal.residuez用法及代碼示例
- Python SciPy signal.bilinear_zpk用法及代碼示例
- Python SciPy signal.firls用法及代碼示例
- Python SciPy signal.impulse用法及代碼示例
- Python SciPy signal.buttord用法及代碼示例
- Python SciPy signal.find_peaks用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.welch。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
