本文简要介绍 python 语言中 scipy.interpolate.approximate_taylor_polynomial 的用法。
用法:
scipy.interpolate.approximate_taylor_polynomial(f, x, degree, scale, order=None)#通过多项式拟合估计 f 在 x 处的泰勒多项式。
- f: 可调用的
寻找泰勒多项式的函数。应该接受 x 值的向量。
- x: 标量
要评估多项式的点。
- degree: int
泰勒多项式的次数
- scale: 标量
用于评估泰勒多项式的区间宽度。分布在如此宽范围内的函数值用于拟合多项式。必须谨慎选择。
- order: int 或无,可选
拟合中使用的多项式的阶数;f将被评估
order+1次。如果没有,使用程度.
- p: poly1d 实例
泰勒多项式(转换为原点,例如 p(0)=f(x))。
参数 ::
返回 ::
注意:
The appropriate choice of “scale” is a trade-off;太大并且函数与其泰勒多项式的差异太大而无法得到一个好的答案,太小和舍入误差会压倒高阶项。即使在理想情况下,所使用的算法也会在 30 阶左右数值不稳定。
选择稍大于度数的阶数可能会改善高阶项。
例子:
我们可以计算各种度数的 sin 函数的泰勒逼近多项式:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import approximate_taylor_polynomial >>> x = np.linspace(-10.0, 10.0, num=100) >>> plt.plot(x, np.sin(x), label="sin curve") >>> for degree in np.arange(1, 15, step=2): ... sin_taylor = approximate_taylor_polynomial(np.sin, 0, degree, 1, ... order=degree + 2) ... plt.plot(x, sin_taylor(x), label=f"degree={degree}") >>> plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', ... borderaxespad=0.0, shadow=True) >>> plt.tight_layout() >>> plt.axis([-10, 10, -10, 10]) >>> plt.show()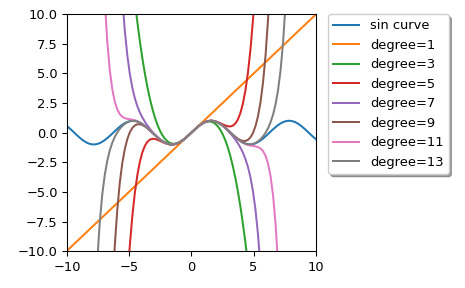
相关用法
- Python SciPy interpolate.make_interp_spline用法及代码示例
- Python SciPy interpolate.krogh_interpolate用法及代码示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代码示例
- Python SciPy interpolate.BSpline用法及代码示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代码示例
- Python SciPy interpolate.griddata用法及代码示例
- Python SciPy interpolate.splder用法及代码示例
- Python SciPy interpolate.LinearNDInterpolator用法及代码示例
- Python SciPy interpolate.PPoly用法及代码示例
- Python SciPy interpolate.NdBSpline用法及代码示例
- Python SciPy interpolate.pade用法及代码示例
- Python SciPy interpolate.barycentric_interpolate用法及代码示例
- Python SciPy interpolate.RegularGridInterpolator用法及代码示例
- Python SciPy interpolate.NdPPoly用法及代码示例
- Python SciPy interpolate.interp2d用法及代码示例
- Python SciPy interpolate.RectSphereBivariateSpline用法及代码示例
- Python SciPy interpolate.sproot用法及代码示例
- Python SciPy interpolate.splantider用法及代码示例
- Python SciPy interpolate.CloughTocher2DInterpolator用法及代码示例
- Python SciPy interpolate.interp1d用法及代码示例
- Python SciPy interpolate.BPoly用法及代码示例
- Python SciPy interpolate.BarycentricInterpolator用法及代码示例
- Python SciPy interpolate.splrep用法及代码示例
- Python SciPy interpolate.make_smoothing_spline用法及代码示例
- Python SciPy interpolate.Rbf用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.interpolate.approximate_taylor_polynomial。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
