Python SciPy interpolate.BarycentricInterpolator用法及代码示例

本文简要介绍 python 语言中 scipy.interpolate.BarycentricInterpolator 的用法。

用法:

class  scipy.interpolate.BarycentricInterpolator(xi, yi=None, axis=0, *, wi=None, random_state=None)#

对一组点进行插值多项式。

构造一个通过给定点集的多项式。允许评估多项式及其所有导数、有效更改要插值的 y-values，以及通过添加更多 x- 和 y-values 进行更新。

出于数值稳定性的原因，该函数不计算多项式的系数。

需要在计算函数之前提供 yi 值，但任何预处理都不依赖于它们，因此可以快速更新。

参数 ：：

xi： 类似数组，形状 (npoints, )

多项式应通过的点的 x 坐标的一维数组

yi： 数组，形状(...，npoints，...)，可选

N-D 多项式应经过的点的 y 坐标数组。如果没有，则 y 值稍后将通过set_y方法。长度为义沿插补轴的长度必须等于xi。使用axis参数来选择正确的轴。

axis： 整数，可选

yi 数组中的轴对应于 x 坐标值。默认为 axis=0 。

wi： 数组，可选

所选插值点 xi 的重心权重。如果不存在或无，则权重将从 xi (默认)计算。如果使用相同节点 xi 计算多个插值，则这允许重新使用权重 wi，而无需重新计算。

random_state： {无，int， numpy.random.Generator ， numpy.random.RandomState }，可选

如果种子是无(或np.random)， 这numpy.random.RandomState使用单例。如果种子是一个 int，一个新的RandomState使用实例，播种种子.如果种子已经是一个Generator或者RandomState实例然后使用该实例。

注意：

此类使用 “barycentric interpolation” 方法，将问题视为有理函数插值的特殊情况。该算法在数值上相当稳定，但即使在精确计算的世界中，除非非常仔细地选择 x 坐标 - 切比雪夫零点(例如，cos(i*pi/n))是一个不错的选择 - 多项式插值本身就是一个由于龙格现象，非常ill-conditioned过程。

基于 Berrut 和 Trefethen 2004 年，“Barycentric Lagrange Interpolation”。

例子：

要生成逼近函数 \(\sin x\) 及其前四个导数的五次重心插值，请使用 \((0, \frac{\pi}{2})\) 中的六个 randomly-spaced 节点：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import BarycentricInterpolator
>>> rng = np.random.default_rng()
>>> xi = rng.random(6) * np.pi/2
>>> f, f_d1, f_d2, f_d3, f_d4 = np.sin, np.cos, lambda x: -np.sin(x), lambda x: -np.cos(x), np.sin
>>> P = BarycentricInterpolator(xi, f(xi), random_state=rng)
>>> fig, axs = plt.subplots(5, 1, sharex=True, layout='constrained', figsize=(7,10))
>>> x = np.linspace(0, np.pi, 100)
>>> axs[0].plot(x, P(x), 'r:', x, f(x), 'k--', xi, f(xi), 'xk')
>>> axs[1].plot(x, P.derivative(x), 'r:', x, f_d1(x), 'k--', xi, f_d1(xi), 'xk')
>>> axs[2].plot(x, P.derivative(x, 2), 'r:', x, f_d2(x), 'k--', xi, f_d2(xi), 'xk')
>>> axs[3].plot(x, P.derivative(x, 3), 'r:', x, f_d3(x), 'k--', xi, f_d3(xi), 'xk')
>>> axs[4].plot(x, P.derivative(x, 4), 'r:', x, f_d4(x), 'k--', xi, f_d4(xi), 'xk')
>>> axs[0].set_xlim(0, np.pi)
>>> axs[4].set_xlabel(r"$x$")
>>> axs[4].set_xticks([i * np.pi / 4 for i in range(5)],
...                   ["0", r"$\frac{\pi}{4}$", r"$\frac{\pi}{2}$", r"$\frac{3\pi}{4}$", r"$\pi$"])
>>> axs[0].set_ylabel("$f(x)$")
>>> axs[1].set_ylabel("$f'(x)$")
>>> axs[2].set_ylabel("$f''(x)$")
>>> axs[3].set_ylabel("$f^{(3)}(x)$")
>>> axs[4].set_ylabel("$f^{(4)}(x)$")
>>> labels = ['Interpolation nodes', 'True function $f$', 'Barycentric interpolation']
>>> axs[0].legend(axs[0].get_lines()[::-1], labels, bbox_to_anchor=(0., 1.02, 1., .102),
...               loc='lower left', ncols=3, mode="expand", borderaxespad=0., frameon=False)
>>> plt.show()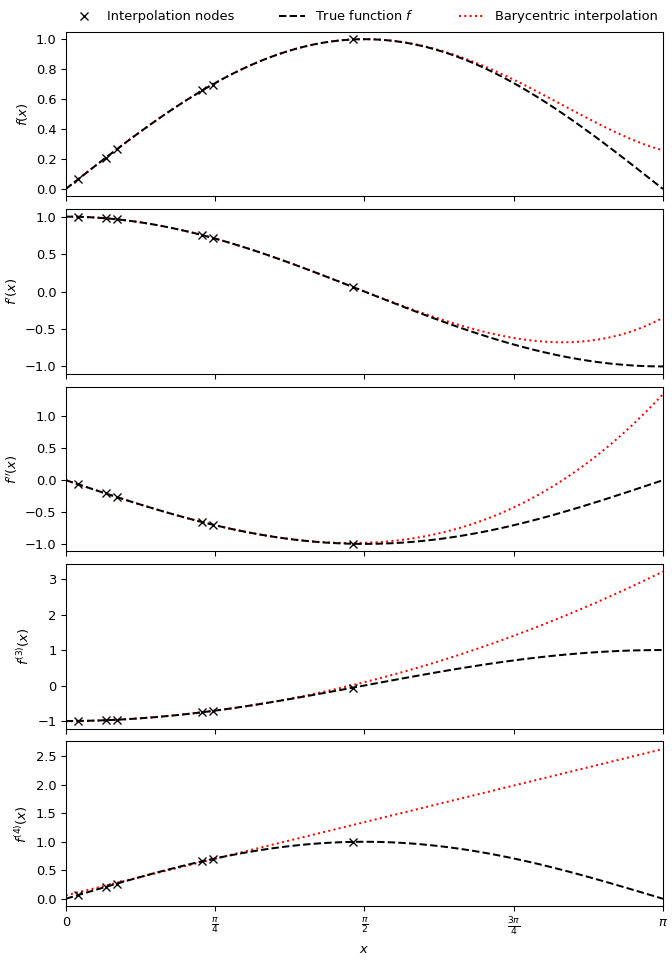

属性 ：：

dtype：