本文简要介绍 python 语言中 scipy.interpolate.make_smoothing_spline 的用法。
用法:
scipy.interpolate.make_smoothing_spline(x, y, w=None, lam=None)#使用
lam计算平滑三次样条函数(的系数),以控制曲线的平滑度与其与数据的接近程度之间的权衡。如果lam为 None,则使用 GCV 标准 [1] 来查找它。找到平滑样条作为正则化加权线性回归问题的解:
其中 是样条函数, 是权重向量, 是正则化参数。
如果
lam为None,我们使用GCV标准来寻找最佳正则化参数,否则我们用给定参数求解正则化加权线性回归问题。参数通过以下方式控制权衡:参数越大,函数越平滑。- x: 数组, 形状 (n,)
横坐标。 n 必须大于 5。
- y: 数组, 形状 (n,)
纵坐标。 n 必须大于 5。
- w: 数组,形状(n,),可选
权重向量。默认为
np.ones_like(x)。- lam: 浮点数,(),可选
正则化参数。如果
lam为None,则从GCV标准中找到。默认为“无”。
- func: BSpline 对象。
表示基于 B-spline 的样条线的可调用函数,作为在
lam为 None 的情况下使用 GCV 标准 [1] 平滑样条线问题的解决方案,否则使用给定参数lam。
参数 ::
返回 ::
注意:
该算法是 Woltring 在 FORTRAN [2] 中引入的算法的干净室重新实现。由于许可证问题,原始版本无法在SciPy源代码中使用。此处讨论了重新实现的细节(仅提供俄语版本)[4]。
如果权重向量
w为None,我们假设所有点的权重相等,并且权重向量是1的向量。请注意,在加权残差平方和中,权重不是平方:,而在
splrep中,总和是根据权重平方构建的。如果初始问题是ill-posed(例如,产品(其中 是设计矩阵)不是正定义矩阵),则会引发ValueError。
参考:
[1]G. Wahba,观测数据样条模型中的“估计平滑参数”,宾夕法尼亚州费城:工业与应用数学学会,1990 年,第 45-65 页。 DOI:10.1137/1.9781611970128
[2]H. J. Woltring,用于广义的 Fortran 包,cross-validatory 样条平滑和微分,工程软件进展,卷。 8、不。 2,第 104-113 页,1986 年。DOI:10.1016/0141-1195(86)90098-7
[3]T. Hastie、J. Friedman 和 R. Tisbshirani,“Smoothing Splines”,《统计学习的要素:数据挖掘、推理和预测》,纽约:Springer,2017 年,第 241-249 页。 DOI:10.1007/978-0-387-84858-7
[4]E. Zemlyanoy,“广义交叉验证平滑样条”,理学学士论文,2022 年。https://www.hse.ru/ba/am/students/diplomas/620910604(俄语)
例子:
生成一些噪声数据
>>> import numpy as np >>> np.random.seed(1234) >>> n = 200 >>> def func(x): ... return x**3 + x**2 * np.sin(4 * x) >>> x = np.sort(np.random.random_sample(n) * 4 - 2) >>> y = func(x) + np.random.normal(scale=1.5, size=n)制作平滑样条函数
>>> from scipy.interpolate import make_smoothing_spline >>> spl = make_smoothing_spline(x, y)绘制两者
>>> import matplotlib.pyplot as plt >>> grid = np.linspace(x[0], x[-1], 400) >>> plt.plot(grid, spl(grid), label='Spline') >>> plt.plot(grid, func(grid), label='Original function') >>> plt.scatter(x, y, marker='.') >>> plt.legend(loc='best') >>> plt.show()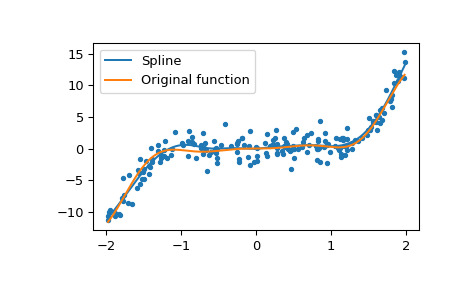
相关用法
- Python SciPy interpolate.make_interp_spline用法及代码示例
- Python SciPy interpolate.make_lsq_spline用法及代码示例
- Python SciPy interpolate.krogh_interpolate用法及代码示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代码示例
- Python SciPy interpolate.BSpline用法及代码示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代码示例
- Python SciPy interpolate.griddata用法及代码示例
- Python SciPy interpolate.splder用法及代码示例
- Python SciPy interpolate.LinearNDInterpolator用法及代码示例
- Python SciPy interpolate.PPoly用法及代码示例
- Python SciPy interpolate.NdBSpline用法及代码示例
- Python SciPy interpolate.pade用法及代码示例
- Python SciPy interpolate.barycentric_interpolate用法及代码示例
- Python SciPy interpolate.RegularGridInterpolator用法及代码示例
- Python SciPy interpolate.NdPPoly用法及代码示例
- Python SciPy interpolate.interp2d用法及代码示例
- Python SciPy interpolate.approximate_taylor_polynomial用法及代码示例
- Python SciPy interpolate.RectSphereBivariateSpline用法及代码示例
- Python SciPy interpolate.sproot用法及代码示例
- Python SciPy interpolate.splantider用法及代码示例
- Python SciPy interpolate.CloughTocher2DInterpolator用法及代码示例
- Python SciPy interpolate.interp1d用法及代码示例
- Python SciPy interpolate.BPoly用法及代码示例
- Python SciPy interpolate.BarycentricInterpolator用法及代码示例
- Python SciPy interpolate.splrep用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.interpolate.make_smoothing_spline。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
