Python SciPy interpolate.make_interp_spline用法及代码示例

本文简要介绍 python 语言中 scipy.interpolate.make_interp_spline 的用法。

用法:

scipy.interpolate.make_interp_spline(x, y, k=3, t=None, bc_type=None, axis=0, check_finite=True)#

计算插值 B-spline 的(系数)。

参数 ：：

x： 数组, 形状 (n,)

横坐标。

y： 数组，形状(n，...)

纵坐标。

k： 整数，可选

B-spline学位。默认为立方体，k = 3 。

t： 数组，形状(nt + k + 1，)，可选。

结。结的数量需要与数据点的数量和边导数的数量一致。具体来说， nt - n 必须等于 len(deriv_l) + len(deriv_r) 。

bc_type： 2 元组或无

边界条件。默认为 None，这意味着自动选择边界条件。否则，它必须是 length-two 元组，其中第一个元素 ( deriv_l ) 在 x[0] 设置边界条件，第二个元素 ( deriv_r ) 在 x[-1] 设置边界条件。其中每个都必须是可迭代的对 (order, value)，它给出插值间隔给定边处指定阶导数的值。或者，可以识别以下字符串别名：

• "clamped"：末端的一阶导数为零。这是

  相当于 bc_type=([(1, 0.0)], [(1, 0.0)]) 。

• "natural"：末端的二阶导数为零。这相当于 bc_type=([(2, 0.0)], [(2, 0.0)]) 。

• "not-a-knot"(默认)：第一段和第二段是相同的多项式。这相当于拥有 bc_type=None 。

• "periodic" ：值和末尾的第一个 k-1 导数是等价的。

axis： 整数，可选

插值轴。默认值为 0。

check_finite： 布尔型，可选

是否检查输入数组是否仅包含有限数。禁用可能会提高性能，但如果输入确实包含无穷大或 NaN，则可能会导致问题(崩溃、非终止)。默认为真。

返回 ：：

b： 度数为 k 并带有结 t 的 BSpline 对象。

例子：

在 Chebyshev 节点上使用三次插值：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def cheb_nodes(N):
...     jj = 2.*np.arange(N) + 1
...     x = np.cos(np.pi * jj / 2 / N)[::-1]
...     return x

>>> x = cheb_nodes(20)
>>> y = np.sqrt(1 - x**2)

>>> from scipy.interpolate import BSpline, make_interp_spline
>>> b = make_interp_spline(x, y)
>>> np.allclose(b(x), y)
True

请注意，默认为具有 not-a-knot 边界条件的三次样条

>>> b.k
3

在这里，我们使用 ‘natural’ 样条曲线，边处的二阶导数为零：

>>> l, r = [(2, 0.0)], [(2, 0.0)]
>>> b_n = make_interp_spline(x, y, bc_type=(l, r))  # or, bc_type="natural"
>>> np.allclose(b_n(x), y)
True
>>> x0, x1 = x[0], x[-1]
>>> np.allclose([b_n(x0, 2), b_n(x1, 2)], [0, 0])
True

还支持参数曲线的插值。例如，我们计算极坐标中蜗牛曲线的离散化

>>> phi = np.linspace(0, 2.*np.pi, 40)
>>> r = 0.3 + np.cos(phi)
>>> x, y = r*np.cos(phi), r*np.sin(phi)  # convert to Cartesian coordinates

构建插值曲线，通过角度对其进行参数化

>>> spl = make_interp_spline(phi, np.c_[x, y])

在更精细的网格上评估插值(请注意，我们转置结果以将其解包为一对 x- 和 y-arrays)

>>> phi_new = np.linspace(0, 2.*np.pi, 100)
>>> x_new, y_new = spl(phi_new).T

绘制结果

>>> plt.plot(x, y, 'o')
>>> plt.plot(x_new, y_new, '-')
>>> plt.show()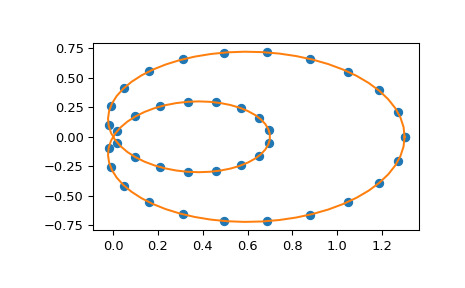

用 2 维 y 构建 B-spline 曲线

>>> x = np.linspace(0, 2*np.pi, 10)
>>> y = np.array([np.sin(x), np.cos(x)])

满足周期性条件，因为两端点的 y 坐标相等

>>> ax = plt.axes(projection='3d')
>>> xx = np.linspace(0, 2*np.pi, 100)
>>> bspl = make_interp_spline(x, y, k=5, bc_type='periodic', axis=1)
>>> ax.plot3D(xx, *bspl(xx))
>>> ax.scatter3D(x, *y, color='red')
>>> plt.show()