本文简要介绍 python 语言中 scipy.integrate.odeint 的用法。
用法:
scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)#积分常微分方程组。
注意
对于新代码,请使用
scipy.integrate.solve_ivp求解微分方程。使用 FORTRAN 库 odepack 中的 lsoda 求解常微分方程组。
求解一阶刚性或非刚性系统的初始值问题 ode-s:
dy/dt = func(y, t, ...) [or func(t, y, ...)]其中 y 可以是一个向量。
注意
默认情况下,前两个参数的所需顺序函数与系统定义函数使用的参数顺序相反scipy.integrate.ode类和函数scipy.integrate.solve_ivp.使用带有签名的函数
func(t, y, ...), 参数第一必须设置为True.- func: callable(y, t, ...) 或 callable(t, y, ...)
计算 y 在 t 处的导数。如果签名是
callable(t, y, ...), 那么参数第一必须设置True.- y0: 数组
y 的初始条件(可以是向量)。
- t: 数组
求解 y 的时间点序列。初始值点应该是这个序列的第一个元素。这个序列必须是单调递增或单调递减的;允许重复值。
- args: 元组,可选
传递给函数的额外参数。
- Dfun: callable(y, t, ...) 或 callable(t, y, ...)
梯度(雅可比)函数.如果签名是
callable(t, y, ...), 那么参数第一必须设置True.- col_deriv: 布尔型,可选
如果 Dfun 定义列下的导数(更快),则为真,否则 Dfun 应跨行定义导数。
- full_output: 布尔型,可选
如果返回可选输出的字典作为第二个输出,则为真
- printmessg: 布尔型,可选
是否打印收敛消息
- tfirst: 布尔型,可选
如果为真,前两个参数函数(和东风, 如果给定) 必须
t, y而不是默认的y, t.
- y: 数组,形状(len(t),len(y0))
包含 t 中每个所需时间的 y 值的数组,初始值 y0 在第一行。
- infodict: dict,仅在 full_output == True 时返回
包含附加输出信息的字典
钥匙
意义
‘hu’
每个时间步成功使用的步长向量
‘tcur’
每个时间步达到 t 值的向量(总是至少与输入时间一样大)
‘tolsf’
大于 1.0 的容差比例因子向量,在检测到精度要求过高时计算
‘tsw’
最后一次方法切换时的 t 值(给定每个时间步)
‘nst’
累计时间步数
‘nfe’
每个时间步的累积函数评估次数
‘nje’
每个时间步的雅可比评估的累积次数
‘nqu’
每个成功步骤的方法顺序向量
‘imxer’
误差返回时加权局部误差向量 (e /ewt) 中最大幅度分量的索引,否则为 -1
‘lenrw’
所需的双工作数组的长度
‘leniw’
所需整数工作数组的长度
‘mused’
每个成功时间步的方法指标向量:1:adams(非刚性),2:bdf(刚性)
- ml, mu: 整数,可选
如果其中任何一个不是 None 或非负数,则假定 Jacobian 是带状的。这些给出了这个带状矩阵中下层和上层非零对角线的数量。对于带状的情况,东风应该返回一个矩阵,其行包含非零带(从最低对角线开始)。因此,返回矩阵江淮从东风应该有形状
(ml + mu + 1, len(y0))当ml >=0或者mu >=0.中的数据江淮必须存储使得jac[i - j + mu, j]持有的导数i第一个方程关于j第一个状态变量。如果col_deriv是真的,这个的转置江淮必须退回。- rtol, atol: 浮点数,可选
输入参数rol和环礁确定求解器执行的误差控制。求解器将根据以下形式的不等式控制 y 中估计的局部误差的向量 e
max-norm of (e / ewt) <= 1,其中 ewt 是正误差权重的向量,计算为ewt = rtol * abs(y) + atol. rtol 和 atol 可以是与 y 长度相同的向量,也可以是标量。默认为 1.49012e-8。- tcrit: ndarray,可选
应注意积分的关键点向量(例如奇异点)。
- h0: 浮点数,(0:solver-determined),可选
第一步要尝试的步长。
- hmax: 浮点数,(0:solver-determined),可选
允许的最大绝对步长。
- hmin: 浮点数,(0:solver-determined),可选
允许的最小绝对步长。
- ixpr: 布尔型,可选
是否在方法切换时生成额外的打印。
- mxstep: 整数,(0:solver-determined),可选
t 中每个积分点允许的最大(内部定义)步数。
- mxhnil: 整数,(0:solver-determined),可选
打印的最大消息数。
- mxordn: 整数,(0:solver-determined),可选
非刚性 (Adams) 方法允许的最大订单。
- mxords: 整数,(0:solver-determined),可选
刚性 (BDF) 方法允许的最大阶数。
参数 ::
返回 ::
其他参数 ::
例子:
受重力和摩擦力作用的摆的角度 theta 的二阶微分方程可以写成:
theta''(t) + b*theta'(t) + c*sin(theta(t)) = 0其中b和c是正常数,素数 (’) 表示导数。求解这个方程
odeint,我们必须首先将其转换为一阶方程组。通过定义角速度omega(t) = theta'(t),我们得到系统:theta'(t) = omega(t) omega'(t) = -b*omega(t) - c*sin(theta(t))设 y 为向量 [theta, omega]。我们用 Python 实现这个系统:
>>> import numpy as np >>> def pend(y, t, b, c): ... theta, omega = y ... dydt = [omega, -b*omega - c*np.sin(theta)] ... return dydt ...我们假设常数是 b = 0.25 和 c = 5.0:
>>> b = 0.25 >>> c = 5.0对于初始条件,我们假设钟摆几乎是垂直的,theta(0) = pi - 0.1,并且最初是静止的,所以 omega(0) = 0。那么初始条件的向量是
>>> y0 = [np.pi - 0.1, 0.0]我们将在 0 <= t <= 10 的区间内以 101 个均匀分布的样本生成一个解。所以我们的时间数组是:
>>> t = np.linspace(0, 10, 101)称呼
odeint生成解决方案。传递参数b和c到挂起,我们给他们odeint使用参数争论。>>> from scipy.integrate import odeint >>> sol = odeint(pend, y0, t, args=(b, c))解决方案是一个形状为 (101, 2) 的数组。第一列是 theta(t),第二列是 omega(t)。以下代码绘制了这两个组件。
>>> import matplotlib.pyplot as plt >>> plt.plot(t, sol[:, 0], 'b', label='theta(t)') >>> plt.plot(t, sol[:, 1], 'g', label='omega(t)') >>> plt.legend(loc='best') >>> plt.xlabel('t') >>> plt.grid() >>> plt.show()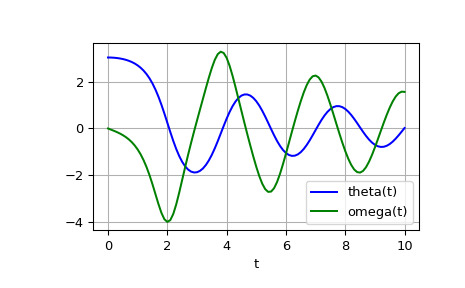
相关用法
- Python SciPy integrate.ode用法及代码示例
- Python SciPy integrate.quad_vec用法及代码示例
- Python SciPy integrate.cumulative_trapezoid用法及代码示例
- Python SciPy integrate.romberg用法及代码示例
- Python SciPy integrate.qmc_quad用法及代码示例
- Python SciPy integrate.dblquad用法及代码示例
- Python SciPy integrate.simpson用法及代码示例
- Python SciPy integrate.quadrature用法及代码示例
- Python SciPy integrate.quad用法及代码示例
- Python SciPy integrate.solve_bvp用法及代码示例
- Python SciPy integrate.solve_ivp用法及代码示例
- Python SciPy integrate.newton_cotes用法及代码示例
- Python SciPy integrate.romb用法及代码示例
- Python SciPy integrate.fixed_quad用法及代码示例
- Python SciPy integrate.tplquad用法及代码示例
- Python SciPy integrate.nquad用法及代码示例
- Python SciPy integrate.trapezoid用法及代码示例
- Python SciPy integrate.quad_explain用法及代码示例
- Python SciPy interpolate.make_interp_spline用法及代码示例
- Python SciPy interpolate.krogh_interpolate用法及代码示例
- Python SciPy interpolative.reconstruct_matrix_from_id用法及代码示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代码示例
- Python SciPy interpolate.BSpline用法及代码示例
- Python SciPy interpolative.reconstruct_interp_matrix用法及代码示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.integrate.odeint。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
