本文簡要介紹 python 語言中 scipy.integrate.odeint 的用法。
用法:
scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)#積分常微分方程組。
注意
對於新代碼,請使用
scipy.integrate.solve_ivp求解微分方程。使用 FORTRAN 庫 odepack 中的 lsoda 求解常微分方程組。
求解一階剛性或非剛性係統的初始值問題 ode-s:
dy/dt = func(y, t, ...) [or func(t, y, ...)]其中 y 可以是一個向量。
注意
默認情況下,前兩個參數的所需順序函數與係統定義函數使用的參數順序相反scipy.integrate.ode類和函數scipy.integrate.solve_ivp.使用帶有簽名的函數
func(t, y, ...), 參數第一必須設置為True.- func: callable(y, t, ...) 或 callable(t, y, ...)
計算 y 在 t 處的導數。如果簽名是
callable(t, y, ...), 那麽參數第一必須設置True.- y0: 數組
y 的初始條件(可以是向量)。
- t: 數組
求解 y 的時間點序列。初始值點應該是這個序列的第一個元素。這個序列必須是單調遞增或單調遞減的;允許重複值。
- args: 元組,可選
傳遞給函數的額外參數。
- Dfun: callable(y, t, ...) 或 callable(t, y, ...)
梯度(雅可比)函數.如果簽名是
callable(t, y, ...), 那麽參數第一必須設置True.- col_deriv: 布爾型,可選
如果 Dfun 定義列下的導數(更快),則為真,否則 Dfun 應跨行定義導數。
- full_output: 布爾型,可選
如果返回可選輸出的字典作為第二個輸出,則為真
- printmessg: 布爾型,可選
是否打印收斂消息
- tfirst: 布爾型,可選
如果為真,前兩個參數函數(和東風, 如果給定) 必須
t, y而不是默認的y, t.
- y: 數組,形狀(len(t),len(y0))
包含 t 中每個所需時間的 y 值的數組,初始值 y0 在第一行。
- infodict: dict,僅在 full_output == True 時返回
包含附加輸出信息的字典
鑰匙
意義
‘hu’
每個時間步成功使用的步長向量
‘tcur’
每個時間步達到 t 值的向量(總是至少與輸入時間一樣大)
‘tolsf’
大於 1.0 的容差比例因子向量,在檢測到精度要求過高時計算
‘tsw’
最後一次方法切換時的 t 值(給定每個時間步)
‘nst’
累計時間步數
‘nfe’
每個時間步的累積函數評估次數
‘nje’
每個時間步的雅可比評估的累積次數
‘nqu’
每個成功步驟的方法順序向量
‘imxer’
誤差返回時加權局部誤差向量 (e /ewt) 中最大幅度分量的索引,否則為 -1
‘lenrw’
所需的雙工作數組的長度
‘leniw’
所需整數工作數組的長度
‘mused’
每個成功時間步的方法指標向量:1:adams(非剛性),2:bdf(剛性)
- ml, mu: 整數,可選
如果其中任何一個不是 None 或非負數,則假定 Jacobian 是帶狀的。這些給出了這個帶狀矩陣中下層和上層非零對角線的數量。對於帶狀的情況,東風應該返回一個矩陣,其行包含非零帶(從最低對角線開始)。因此,返回矩陣江淮從東風應該有形狀
(ml + mu + 1, len(y0))當ml >=0或者mu >=0.中的數據江淮必須存儲使得jac[i - j + mu, j]持有的導數i第一個方程關於j第一個狀態變量。如果col_deriv是真的,這個的轉置江淮必須退回。- rtol, atol: 浮點數,可選
輸入參數rol和環礁確定求解器執行的誤差控製。求解器將根據以下形式的不等式控製 y 中估計的局部誤差的向量 e
max-norm of (e / ewt) <= 1,其中 ewt 是正誤差權重的向量,計算為ewt = rtol * abs(y) + atol. rtol 和 atol 可以是與 y 長度相同的向量,也可以是標量。默認為 1.49012e-8。- tcrit: ndarray,可選
應注意積分的關鍵點向量(例如奇異點)。
- h0: 浮點數,(0:solver-determined),可選
第一步要嘗試的步長。
- hmax: 浮點數,(0:solver-determined),可選
允許的最大絕對步長。
- hmin: 浮點數,(0:solver-determined),可選
允許的最小絕對步長。
- ixpr: 布爾型,可選
是否在方法切換時生成額外的打印。
- mxstep: 整數,(0:solver-determined),可選
t 中每個積分點允許的最大(內部定義)步數。
- mxhnil: 整數,(0:solver-determined),可選
打印的最大消息數。
- mxordn: 整數,(0:solver-determined),可選
非剛性 (Adams) 方法允許的最大訂單。
- mxords: 整數,(0:solver-determined),可選
剛性 (BDF) 方法允許的最大階數。
參數 ::
返回 ::
其他參數 ::
例子:
受重力和摩擦力作用的擺的角度 theta 的二階微分方程可以寫成:
theta''(t) + b*theta'(t) + c*sin(theta(t)) = 0其中b和c是正常數,素數 (’) 表示導數。求解這個方程
odeint,我們必須首先將其轉換為一階方程組。通過定義角速度omega(t) = theta'(t),我們得到係統:theta'(t) = omega(t) omega'(t) = -b*omega(t) - c*sin(theta(t))設 y 為向量 [theta, omega]。我們用 Python 實現這個係統:
>>> import numpy as np >>> def pend(y, t, b, c): ... theta, omega = y ... dydt = [omega, -b*omega - c*np.sin(theta)] ... return dydt ...我們假設常數是 b = 0.25 和 c = 5.0:
>>> b = 0.25 >>> c = 5.0對於初始條件,我們假設鍾擺幾乎是垂直的,theta(0) = pi - 0.1,並且最初是靜止的,所以 omega(0) = 0。那麽初始條件的向量是
>>> y0 = [np.pi - 0.1, 0.0]我們將在 0 <= t <= 10 的區間內以 101 個均勻分布的樣本生成一個解。所以我們的時間數組是:
>>> t = np.linspace(0, 10, 101)稱呼
odeint生成解決方案。傳遞參數b和c到掛起,我們給他們odeint使用參數爭論。>>> from scipy.integrate import odeint >>> sol = odeint(pend, y0, t, args=(b, c))解決方案是一個形狀為 (101, 2) 的數組。第一列是 theta(t),第二列是 omega(t)。以下代碼繪製了這兩個組件。
>>> import matplotlib.pyplot as plt >>> plt.plot(t, sol[:, 0], 'b', label='theta(t)') >>> plt.plot(t, sol[:, 1], 'g', label='omega(t)') >>> plt.legend(loc='best') >>> plt.xlabel('t') >>> plt.grid() >>> plt.show()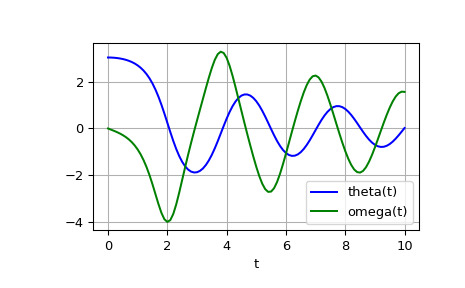
相關用法
- Python SciPy integrate.ode用法及代碼示例
- Python SciPy integrate.quad_vec用法及代碼示例
- Python SciPy integrate.cumulative_trapezoid用法及代碼示例
- Python SciPy integrate.romberg用法及代碼示例
- Python SciPy integrate.qmc_quad用法及代碼示例
- Python SciPy integrate.dblquad用法及代碼示例
- Python SciPy integrate.simpson用法及代碼示例
- Python SciPy integrate.quadrature用法及代碼示例
- Python SciPy integrate.quad用法及代碼示例
- Python SciPy integrate.solve_bvp用法及代碼示例
- Python SciPy integrate.solve_ivp用法及代碼示例
- Python SciPy integrate.newton_cotes用法及代碼示例
- Python SciPy integrate.romb用法及代碼示例
- Python SciPy integrate.fixed_quad用法及代碼示例
- Python SciPy integrate.tplquad用法及代碼示例
- Python SciPy integrate.nquad用法及代碼示例
- Python SciPy integrate.trapezoid用法及代碼示例
- Python SciPy integrate.quad_explain用法及代碼示例
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy interpolative.reconstruct_matrix_from_id用法及代碼示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代碼示例
- Python SciPy interpolate.BSpline用法及代碼示例
- Python SciPy interpolative.reconstruct_interp_matrix用法及代碼示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.integrate.odeint。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
