Python SciPy integrate.solve_ivp用法及代碼示例

本文簡要介紹 python 語言中 scipy.integrate.solve_ivp 的用法。

用法:

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options)#

求解 ODE 係統的初始值問題。

該函數對給定初始值的常微分方程組進行數值積分：

dy / dt = f(t, y)
y(t0) = y0

這裏 t 是一維自變量(時間)，y(t) 是N-D vector-valued 函數(狀態)，N-D vector-valued 函數 f(t, y) 確定微分方程。目標是在給定初始值 y(t0)=y0 的情況下找到近似滿足微分方程的 y(t)。

一些求解器支持複數域中的積分，但請注意，對於剛性 ODE 求解器，右側必須是 complex-differentiable(滿足 Cauchy-Riemann 方程 [11])。要解決複雜域中的問題，請傳遞具有複雜數據類型的 y0。另一個始終可用的選擇是分別重寫實部和虛部的問題。

參數 ：：

fun： 可調用的

係統右側：狀態的時間導數y在某個時間t。調用簽名是fun(t, y)，其中t是一個標量並且y是一個 ndarraylen(y) = len(y0)。需要傳遞額外的參數，如果args使用(參見文檔args爭論)。fun必須返回與以下形狀相同的數組y.看矢量化了解更多信息。

t_span： 2元序列

積分間隔(t0，tf)。求解器從 t=t0 開始進行積分，直到達到 t=tf。 t0 和 tf 都必須是浮點數或可由浮點轉換函數解釋的值。

y0： 數組, 形狀 (n,)

初始狀態。對於複雜域中的問題，使用複雜數據類型傳遞 y0(即使初始值是純實數)。

method： 字符串或 OdeSolver ，可選

使用的積分方法：

• ‘RK45’ (default): Explicit Runge-Kutta method of order 5(4) [1]. The error is controlled assuming accuracy of the fourth-order method, but steps are taken using the fifth-order accurate formula (local extrapolation is done). A quartic interpolation polynomial is used for the dense output [2]. Can be applied in the complex domain.

• ‘RK23’: Explicit Runge-Kutta method of order 3(2) [3]. The error is controlled assuming accuracy of the second-order method, but steps are taken using the third-order accurate formula (local extrapolation is done). A cubic Hermite polynomial is used for the dense output. Can be applied in the complex domain.

• ‘DOP853’: Explicit Runge-Kutta method of order 8 [13]. Python implementation of the “DOP853” algorithm originally written in Fortran [14]. A 7-th order interpolation polynomial accurate to 7-th order is used for the dense output. Can be applied in the complex domain.

• ‘Radau’: Implicit Runge-Kutta method of the Radau IIA family of order 5 [4]. The error is controlled with a third-order accurate embedded formula. A cubic polynomial which satisfies the collocation conditions is used for the dense output.

• ‘BDF’: Implicit multi-step variable-order (1 to 5) method based on a backward differentiation formula for the derivative approximation [5]. The implementation follows the one described in [6]. A quasi-constant step scheme is used and accuracy is enhanced using the NDF modification. Can be applied in the complex domain.

• ‘LSODA’: Adams/BDF method with automatic stiffness detection and switching [7], [8]. This is a wrapper of the Fortran solver from ODEPACK.

顯式 Runge-Kutta 方法(‘RK23’、‘RK45’、‘DOP853’)應用於非剛性問題，隱式方法(‘Radau’、‘BDF’)應用於剛性問題[9].在Runge-Kutta 方法中，推薦使用‘DOP853’進行高精度求解(低值rol和環礁)。

如果不確定，請先嘗試運行“RK45”。如果它進行異常多次迭代、發散或失敗，您的問題可能會很僵硬，您應該使用“Radau”或“BDF”。 “LSODA”也可以是一個很好的通用選擇，但使用它可能不太方便，因為它包裝了舊的 Fortran 代碼。

您還可以傳遞從實現求解器的 OdeSolver 派生的任意類。

t_eval： 數組 或 None，可選

存儲計算解決方案的時間必須排序並位於 t_span 內。如果無(默認)，則使用求解器選擇的點。

dense_output： 布爾型，可選

是否計算連續解。默認為假。

events： 可調用的，或可調用的列表，可選

要跟蹤的事件。如果 None(默認)，則不會跟蹤任何事件。每個事件都發生在時間和狀態的連續函數的零點處。每個函數都必須有簽名event(t, y)如果必須傳遞附加參數args使用(參見文檔args爭論)。每個函數必須返回一個浮點數。求解器將找到一個準確的值t在哪個event(t, y(t)) = 0使用root-finding 算法。默認情況下，將找到所有零。求解器會在每個步驟中尋找符號變化，因此如果在一個步驟中發生多個過零，則可能會錯過事件。另外每個事件函數可能具有以下屬性：

terminal: bool, optional

Whether to terminate integration if this event occurs. Implicitly False if not assigned.

direction: float, optional

Direction of a zero crossing. If direction is positive, event will only trigger when going from negative to positive, and vice versa if direction is negative. If 0, then either direction will trigger event. Implicitly 0 if not assigned.

您可以將 event.terminal = True 等屬性分配給 Python 中的任何函數。

vectorized： 布爾型，可選

是否可以以矢量化方式調用樂趣。默認值為 False。

如果vectorized是假的，樂趣總是會被調用y形狀的(n,)，其中n = len(y0).

如果vectorized是真的，樂趣可以調用y形狀的(n, k)，其中k是一個整數。在這種情況下，樂趣必須表現得這樣fun(t, y)[:, i] == fun(t, y[:, i])(即返回數組的每一列都是與一列對應的狀態的時間導數y)。

設置vectorized=True允許通過方法“Radau”和“BDF”更快地進行雅可比行列式的有限差分近似，但在某些情況下會導致其他方法以及“Radau”和“BDF”的執行速度變慢(例如小len(y0) )。

args： 元組，可選

傳遞給用戶定義函數的附加參數。如果給定，附加參數將傳遞給所有用戶定義的函數。因此，例如，如果樂趣有簽名fun(t, y, a, b, c)， 然後江淮(如果給定)並且任何事件函數必須具有相同的簽名，並且參數必須是長度為 3 的元組。

**options：

傳遞給選定求解器的選項。下麵列出了已實現求解器的所有可用選項。

first_step： 浮點數或無，可選

初始步長。默認為無，這意味著算法應該選擇。

max_step： 浮點數，可選

最大允許步長。默認值為 np.inf，即步長不受限製，僅由求解器確定。

rtol, atol： float 或 數組，可選

相對和絕對公差。求解器保持局部誤差估計小於atol + rtol * abs(y).這裏rol控製相對精度(正確位數)，而環礁控製絕對精度(正確的小數位數)。達到預期rol， 放環礁小於可以預期的最小值rtol * abs(y)以便rol支配允許誤差。如果環礁大於rtol * abs(y)不保證正確位數。反之，達到預期環礁setrol這樣rtol * abs(y)總是小於環礁.如果 y 的分量具有不同的尺度，則設置不同的尺度可能是有益的環礁通過將 數組 與 shape (n,) 傳遞給不同組件的值環礁.默認值為 1e-3rol和 1e-6 為環礁.

jac： 數組，sparse_matrix，可調用或無，可選

“Radau”、“BDF”和“LSODA”方法所需的係統右側關於 y 的雅可比矩陣。雅可比矩陣的形狀為 (n, n)，其元素 (i, j) 等於 d f_i / d y_j 。定義雅可比行列式有以下三種方法：

• If array_like or sparse_matrix, the Jacobian is assumed to be constant. Not supported by ‘LSODA’.

• If callable, the Jacobian is assumed to depend on both t and y; it will be called as jac(t, y), as necessary. Additional arguments have to be passed if args is used (see documentation of args argument). For ‘Radau’ and ‘BDF’ methods, the return value might be a sparse matrix.

• If None (default), the Jacobian will be approximated by finite differences.

通常建議提供雅可比行列式而不是依賴有限差分近似。

jac_sparsity： 數組，稀疏矩陣或無，可選

為有限差分近似定義雅可比矩陣的稀疏結構。它的形狀必須是 (n, n)。如果江淮不是None.如果雅可比矩陣中隻有少數非零元素每個行，提供稀疏結構將大大加快計算速度[10].零條目意味著雅可比矩陣中的相應元素始終為零。如果無(默認)，則假定雅可比是密集的。 “LSODA”不支持，請參閱帶和烏班反而。

lband, uband： int 或無，可選

定義“LSODA”方法的雅可比帶寬的參數，即 jac[i, j] != 0 only for i - lband <= j <= i + uband 。默認為無。設置這些要求您的 jac 例程以打包格式返回雅可比行列式：返回的數組必須具有 n 列和 uband + lband + 1 行，其中寫入雅可比對角線。特別是 jac_packed[uband + i - j , j] = jac[i, j] 。 scipy.linalg.solve_banded 使用相同的格式(查看插圖)。這些參數也可以與jac=None 一起使用，以減少通過有限差分估計的雅可比元素的數量。

min_step： 浮點數，可選

“LSODA”方法的最小允許步長。默認情況下 min_step 為零。

返回 ：：

定義了以下字段的 Bunch 對象：

t： ndarray，形狀(n_points，)

時間點。

y： ndarray，形狀(n，n_points)

t 處解的值。

sol： OdeSolution 或無

找到解決方案為OdeSolution實例;沒有如果dense_output被設置為假。

t_events： ndarray 或無列表

包含每個事件類型的數組列表，在該列表中檢測到該類型事件的事件。如果事件為無，則無。

y_events： ndarray 或無列表

對於 t_events 的每個值，解的對應值。如果事件為無，則無。

nfev： int

右側的評估次數。

njev： int

雅可比的評估次數。

nlu： int

LU 分解的數量。

status： int

算法終止原因：

• -1: Integration step failed.

• 0: The solver successfully reached the end of tspan.

• 1: A termination event occurred.

message： string

終止原因的人類可讀說明。

success： bool

如果求解器達到間隔結束或發生終止事件 (status >= 0)，則為真。

參考：

[1]

J. R. Dormand, P. J. Prince，“一係列嵌入式Runge-Kutta 公式”，計算與應用數學雜誌，卷。 6，第 1 期，第 19-26 頁，1980 年。

[2]

L. W. Shampine，“一些實用的Runge-Kutta 公式”，計算數學，卷。 46，第 173 期，第 135-150 頁，1986 年。

[3]

P. Bogacki, L.F. Shampine，“A 3(2) Pair of Runge-Kutta Formulas”，Appl。數學。萊特。卷。 2，第 4 期。第 321-325 頁，1989 年。

[4]

E. Hairer, G. Wanner，“求解常微分方程 II：剛性和 Differential-Algebraic 問題”，秒。 IV.8.

[5]

Backward Differentiation Formula 在維基百科上。

[6]

L. F. Shampine，M. W. Reichelt，“MATLAB ODE 套件”，SIAM J. SCI。計算，卷。 18，第 1 期，第 1-22 頁，1997 年 1 月。

[7]

A. C. Hindmarsh，“ODEPACK，ODE 求解器的係統化集合”，IMACS Transactions on Scientific Computation，第 1 卷，第 55-64 頁，1983 年。

[8]

L. Petzold，“自動選擇求解常微分方程的剛性和非剛性係統的方法”，SIAM 科學與統計計算雜誌，卷。 4，第 1 期，第 136-148 頁，1983 年。

[9]

Stiff equation 在維基百科上。

[10]

A. Curtis、M. J. D. Powell 和 J. Reid，“關於稀疏雅可比矩陣的估計”，數學研究所及其應用雜誌，13，第 117-120 頁，1974 年。

[11]

Cauchy-Riemann equations 在維基百科上。

[12]

Lotka-Volterra equations 在維基百科上。

[13]

E. Hairer, S. P. Norsett G. Wanner，“求解常微分方程 I：非剛性問題”，秒。二、

[14]

Page with original Fortran code of DOP853 。

例子：

顯示自動選擇的時間點的基本 index 衰減。

>>> import numpy as np
>>> from scipy.integrate import solve_ivp
>>> def exponential_decay(t, y): return -0.5 * y
>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8])
>>> print(sol.t)
[ 0.          0.11487653  1.26364188  3.06061781  4.81611105  6.57445806
  8.33328988 10.        ]
>>> print(sol.y)
[[2.         1.88836035 1.06327177 0.43319312 0.18017253 0.07483045
  0.03107158 0.01350781]
 [4.         3.7767207  2.12654355 0.86638624 0.36034507 0.14966091
  0.06214316 0.02701561]
 [8.         7.5534414  4.25308709 1.73277247 0.72069014 0.29932181
  0.12428631 0.05403123]]

指定需要解決方案的點。

>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8],
...                 t_eval=[0, 1, 2, 4, 10])
>>> print(sol.t)
[ 0  1  2  4 10]
>>> print(sol.y)
[[2.         1.21305369 0.73534021 0.27066736 0.01350938]
 [4.         2.42610739 1.47068043 0.54133472 0.02701876]
 [8.         4.85221478 2.94136085 1.08266944 0.05403753]]

大炮在撞擊時向上發射並帶有終端事件。事件的terminal 和direction 字段是通過猴子修補函數來應用的。這裏y[0] 是位置，y[1] 是速度。彈丸從位置 0 開始，速度 +10。請注意，積分永遠不會達到 t=100，因為事件是終端。

>>> def upward_cannon(t, y): return [y[1], -0.5]
>>> def hit_ground(t, y): return y[0]
>>> hit_ground.terminal = True
>>> hit_ground.direction = -1
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10], events=hit_ground)
>>> print(sol.t_events)
[array([40.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]

采用dense_output和事件找到炮彈軌跡頂點的位置，即 100。 Apex 未定義為終端，因此找到了 apex 和 hit_ground。 t=20 時沒有信息，所以使用 sol 屬性來評估解。 sol 屬性通過設置返回dense_output=True.或者，y_events屬性可用於在事件發生時訪問解決方案。

>>> def apex(t, y): return y[1]
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10],
...                 events=(hit_ground, apex), dense_output=True)
>>> print(sol.t_events)
[array([40.]), array([20.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]
>>> print(sol.sol(sol.t_events[1][0]))
[100.   0.]
>>> print(sol.y_events)
[array([[-5.68434189e-14, -1.00000000e+01]]), array([[1.00000000e+02, 1.77635684e-15]])]

作為具有附加參數的係統的示例，我們將實現Lotka-Volterra 方程 [12]。

>>> def lotkavolterra(t, z, a, b, c, d):
...     x, y = z
...     return [a*x - b*x*y, -c*y + d*x*y]
...

我們使用 args 參數傳入參數值 a=1.5、b=1、c=3 和 d=1。

>>> sol = solve_ivp(lotkavolterra, [0, 15], [10, 5], args=(1.5, 1, 3, 1),
...                 dense_output=True)

計算一個稠密的解決方案並繪製它。

>>> t = np.linspace(0, 15, 300)
>>> z = sol.sol(t)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, z.T)
>>> plt.xlabel('t')
>>> plt.legend(['x', 'y'], shadow=True)
>>> plt.title('Lotka-Volterra System')
>>> plt.show()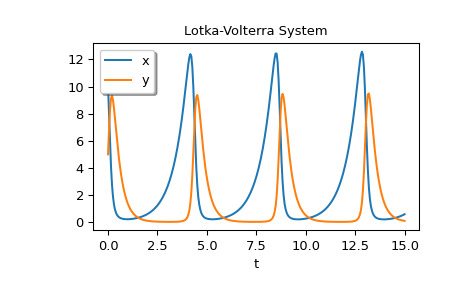

使用 solve_ivp 求解具有複數矩陣 A 的微分方程 y' = Ay 的幾個示例。

>>> A = np.array([[-0.25 + 0.14j, 0, 0.33 + 0.44j],
...               [0.25 + 0.58j, -0.2 + 0.14j, 0],
...               [0, 0.2 + 0.4j, -0.1 + 0.97j]])

使用上麵的 A 和 y 作為 3x1 向量求解 IVP：

>>> def deriv_vec(t, y):
...     return A @ y
>>> result = solve_ivp(deriv_vec, [0, 25],
...                    np.array([10 + 0j, 20 + 0j, 30 + 0j]),
...                    t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0])
[10.+0.j 20.+0.j 30.+0.j]
>>> print(result.y[:, -1])
[18.46291039+45.25653651j 10.01569306+36.23293216j
 -4.98662741+80.07360388j]

使用上麵的 A 求解 IVP，並將 y 作為 3x3 矩陣：

>>> def deriv_mat(t, y):
...     return (A @ y.reshape(3, 3)).flatten()
>>> y0 = np.array([[2 + 0j, 3 + 0j, 4 + 0j],
...                [5 + 0j, 6 + 0j, 7 + 0j],
...                [9 + 0j, 34 + 0j, 78 + 0j]])

>>> result = solve_ivp(deriv_mat, [0, 25], y0.flatten(),
...                    t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0].reshape(3, 3))
[[ 2.+0.j  3.+0.j  4.+0.j]
 [ 5.+0.j  6.+0.j  7.+0.j]
 [ 9.+0.j 34.+0.j 78.+0.j]]
>>> print(result.y[:, -1].reshape(3, 3))
[[  5.67451179 +12.07938445j  17.2888073  +31.03278837j
    37.83405768 +63.25138759j]
 [  3.39949503 +11.82123994j  21.32530996 +44.88668871j
    53.17531184+103.80400411j]
 [ -2.26105874 +22.19277664j -15.1255713  +70.19616341j
   -38.34616845+153.29039931j]]