MNIST Tensorflow新手教程

本教程面向刚学习机器学习和TensorFlow的读者。如果您已经知道MNIST是什么，以及softmax(多项式逻辑)回归是什么，那么您可以跳到节奏更快的教程。在开始任何教程之前务必安装TensorFlow。

当学习如何编程时，首先要做的就是打印“Hello World”。编程起步有Hello World，而机器学习起步就是MNIST。

MNIST是一个简单的计算机视觉数据集。它由这样的手写数字的图像组成：

它还包括每个图像的标签，告诉我们它是哪个数字。例如，上述图像的标签是5,0,4和1。

在本教程中，我们将训练一个模型来查看图像并预测它们是什么数字。我们的目标不是训练一个能够达到state-of-the-art表现的精心制作的模型 – 尽管我们稍后会给您提供代码！ – 而是倾向于让您学会TensorFlow的入门级用法。因此，我们将从一个非常简单的模型开始，称为Softmax回归。

本教程的实际代码非常短，所有有趣的东西都只发生在三行中。然而，了解其背后的理念非常重要：TensorFlow的工作原理和核心机器学习概念。正因为如此，我们要非常小心的走查代码。

关于本教程

这个教程是对这个文件一行一行的代码解释。

您可以通过几种不同的方式使用本教程，其中包括：

• 阅读每行的解释时，将每个代码段逐行复制并粘贴到Python环境中。
• 在阅读解释之前或之后，运行整个mnist_softmax.pyPython文件，并使用本教程来理解不清楚的代码行。

我们将在本教程中完成的任务：

• 了解MNIST数据和softmax回归
• 根据查看图像中的每个像素，创建一个识别数字的模型
• 使用TensorFlow训练模型，通过查看数千个示例来识别数字(并运行我们的第一个TensorFlow会话来完成)
• 用我们的测试数据检查模型的准确性

MNIST数据

MNIST数据托管在Yann LeCun的网站。如果您正在复制和粘贴本教程中的代码，请从这里开始这两行代码，它们将自动下载并读取数据：

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

MNIST数据分为三部分：55,000个训练数据的数据点(mnist.train)，10000点的测试数据(mnist.test)和5,000点验证数据(mnist.validation)。这种分裂是非常重要的：机器学习中必须具备我们不能从中学习的独立数据，这样我们才能确保我们学到的东西实际上可泛化的！

如前所述，每个MNIST数据点有两部分：一个手写数字的图像和一个相应的标签。我们将调用图像”x”和标签”y”。训练集和测试集都包含图像及其相应的标签;例如训练图像是mnist.train.images和训练标签是mnist.train.labels。

每个图像是28像素×28像素。我们可以把它解释为一大堆数字：

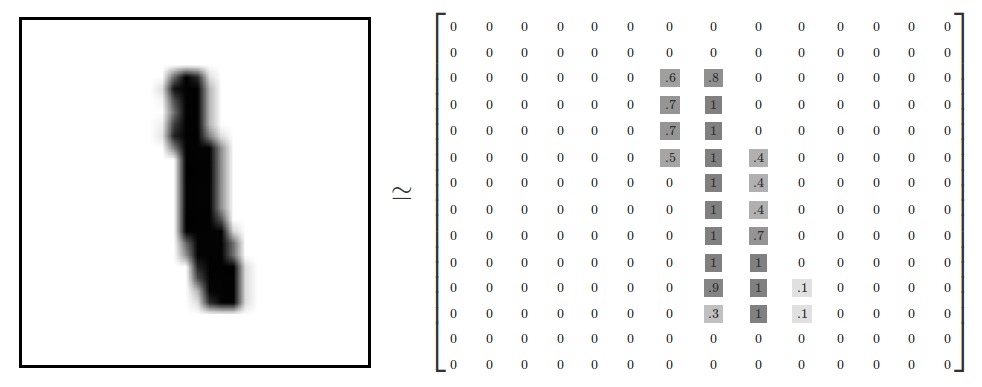
我们可以把这个数组变成一个28×28 = 784的数字。只要我们在图像之间保持一致，那么我们如何展开阵列并不重要。从这个角度来看，MNIST图像只是784维向量空间中的一束点，结构非常丰富(警告：计算密集的可视化)。

展平数据会丢弃有关图像二维结构的信息。这可能是有问题的，但是，最好的计算机视觉方法就是可以利用这个结构的，我们将在后面的教程中介绍。在这里只使用的简单方法，softmax回归(下面定义)。

结果就是这样：mnist.train.images是一个张量(n-dimensional阵列)，形状是[55000, 784]。第一维是图像列表的索引，第二维是每个图像中每个像素的索引。张量中的每个条目是针对特定图像中的特定像素的介于0和1之间的像素强度。

MNIST中的每个图像都有相应的标签，0到9之间的数字代表图像中绘制的数字。

为了本教程的目的，我们将要求我们的标签为“one-hot vectors”。 one-hot向量是一个在大多数维度上为0，在一个维度上为1的向量。在这种情况下，第n个数字将被表示为在第n维中为1的向量。例如，3将是[0,0,0,1,0,0,0,0,0,0]。所以，mnist.train.labels是一个[55000, 10]浮点数阵列。

Softmax回归

我们知道MNIST中的每个图像都是一个0到9之间的手写数字。所以一个给定的图像可能只有十个可能的东西。我们希望能够看到一个图像，并给出它是每个数字的概率。例如，我们的模型可能会查看一张9的图片，并且有80％确定这是一张9的图片，但是给出一个5％的概率是因为它是一个8(因为顶部循环)，并且对所有其他的概率有一点概率，这不是100％确定。

这是说明softmax回归是一个自然，简单模型的经典案例。如果你想把一个对象的概率分配给几个不同的东西之一，softmax就是要做的事情，因为softmax给了我们一个0到1之间的数值列表，加起来就是1。后续，当我们训练更复杂的模型，最后一步仍然会是一个softmax层。

softmax回归有两个步骤：首先我们将输入的证据加在某些类别中，然后将证据转换成概率。

为了收集给定图像在特定类别中的证据，我们进行像素强度的加权总和。如果具有高强度的像素是针对在该类别中的图像的证据，则权重是负的;如果证据是有利的，则权重是正的。

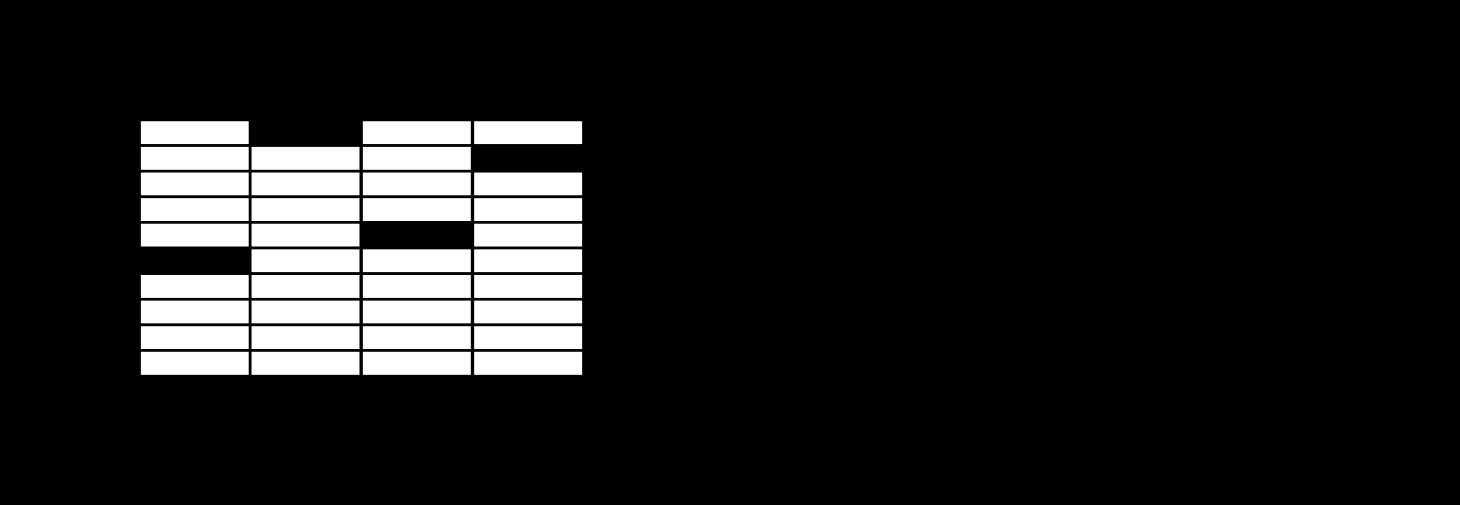
下图显示了一个模型为每个类学习的权重。红色代表负面权重，蓝色代表正面权重。

我们还添加了一些额外的证据，称为偏置。基本上，我们希望能够说有些东西更可能独立于输入。结果是给定输入x的属于类i的证据是：

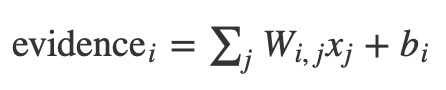
其中w_i是权重，b_i是类别i的偏差，j是对输入图像中的像素进行求和的索引。然后，我们使用”softmax”函数将证据符号转换成我们的预测概率y：

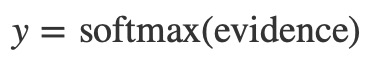
在这里，softmax用作”activation”或”link”函数，将线性函数的输出整形成我们想要的形式 – 在这种情况下，概率分布超过10种情况。你可以把它看作是将证据的转换转化为我们在每个类中投入的概率。它被定义为：

如果将这个等式展开，你会得到：

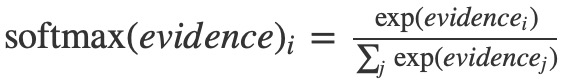
但是，按第一种方式考虑softmax是更有帮助的：指数化输入，然后使其正则化。指数意味着多一个单位的证据增加了任何假设乘加的权重。而相反，少一个证据单位意味着一个假设获得了早期权重的一小部分。没有假设曾经有零或负权重。 Softmax然后归一化这些权重，使它们加起来为1，形成有效的概率分布。 (为了得到关于softmax函数的更多知识，参考部分在迈克尔·尼尔森的书中，有一个互动的可视化。)

您可以将我们的softmax回归看成如下所示，尽管有更多x。对于每个输出，我们计算x的加权和，加一个偏差，然后应用softmax。

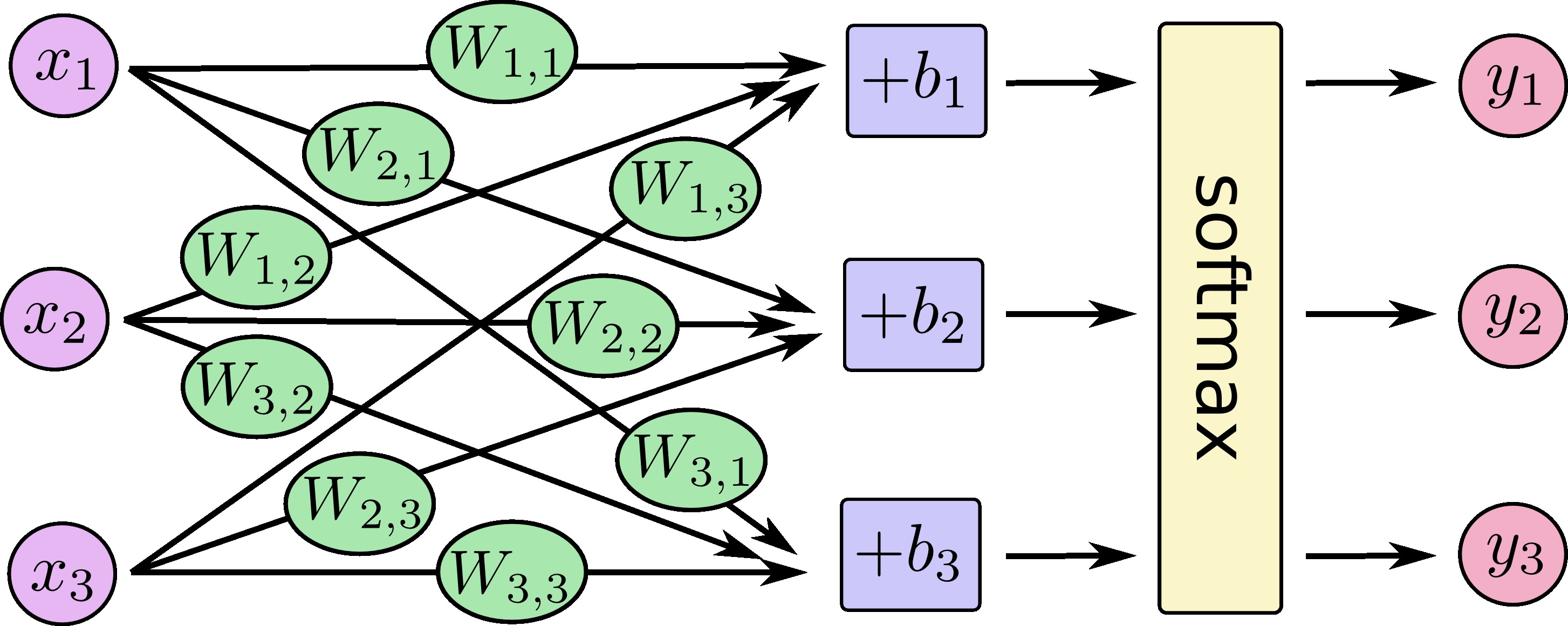
如果我们把它写成等式，我们得到：

我们可以用”vectorize”这个程序，把它变成一个矩阵乘法和矢量加法，从而提升计算性能。

更简洁，我们可以写：

现在让我们把它转换成TensorFlow可以使用的东西。

实现回归

为了在Python中进行高效的数值计算，我们通常使用NumPy一类的库，在Python之外执行耗时的操作，例如矩阵乘法，使用以另一种语言实现的高效代码。不幸的是，每一次操作都会返回到Python，这仍然会有很多开销。如果要在GPU上运行计算或以分布式方式运行计算，则传输数据的成本更高，所以此开销尤其糟糕。

TensorFlow也在Python之外进行繁重的工作，但是为了避免这种开销，还需要进一步的工作。 TensorFlow不是独立于Python运行一个昂贵的操作，而是让我们描述一个完全在Python之外运行的交互操作图。 (像这样的方法也可以在其他几个机器学习库中看到)

要使用TensorFlow，首先我们需要导入它。

import tensorflow as tf

我们通过操纵符号变量来描述这些交互操作。我们来创建一个：

x = tf.placeholder(tf.float32, [None, 784])

x不是一个具体的值。它是placeholder，当我们要求TensorFlow运行一个计算时，我们将输入一个值。我们希望能够输入任意数量的MNIST图像，每个图像被平面化成784维向量。我们将其表示为floating-point数字的二维张量[None, 784]。 (这里None意味着尺寸可以是任意长度。)

我们也需要我们的模型的权重和偏置。我们可以想象把这些看作是额外的投入，但TensorFlow有一个更好的方法来处理它：Variable。一个Variable是在TensorFlow的交互操作图中的可修改的张量。它可以被使用，甚至被计算修改。对于机器学习应用，模型参数通常定义为Variable。

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

我们创造这些Variables，通过给予tf.Variable初始值的方式：在这种情况下，我们初始化W和b作为充满零的张量。既然我们要学到W和b的理想值，它们最初的内容并不重要。

注意到W具有[784，10]的形状，因为我们想通过乘以784维图像向量来产生区分类别的证据的10维向量。b具有[10]的形状，所以我们可以将其添加到输出。

我们现在可以实现我们的模型。只需要一行来定义它！

y = tf.nn.softmax(tf.matmul(x, W) + b)

首先，我们通过表达式tf.matmul(x, W)将x和W相乘。这是从方程中乘以它们的时候翻转过来的，在那里我们有了(Wx)，作为一个小技巧来处理x是具有多个输入的2D张量。然后我们添加b，最后应用tf.nn.softmax。

就这么简单。经过几行简单的设置之后，我们只用一行代码来定义我们的模型。这并不是因为TensorFlow被设计成使得softmax回归特别容易：从机器学习模型到物理模拟，这只是描述多种数值计算的一种非常灵活的方式。一旦定义，我们的模型可以在不同的设备上运行：计算机的CPU，GPU甚至是手机！

训练

为了训练我们的模型，我们需要定义模型的好坏标准。实际上，在机器学习中，我们通常定义一个模型的坏处，我们称之为成本或损失，它表示我们的模型离我们期望的结果有多远。我们尽量减少这个误差，误差越小，我们的模型就越好。

一个非常常见损失函数被称为”cross-entropy.” Cross-entropy产生于信息论中的信息压缩代码的思想，但它是从赌博到机器学习的很多领域，作为一个重要的想法。它被定义为：

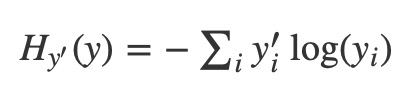
其中y是我们预测的概率分布，而y’是真正的分布(具有数字标签的one-hot向量)。在一些粗略的意义上，cross-entropy正在测量我们的预测是如何低效的来描述真相。有关cross-entropy的更多细节超出了本教程的范围，但它非常值得理解。

要实现cross-entropy，我们需要先添加一个新的占位符来输入正确的答案：

y_ = tf.placeholder(tf.float32, [None, 10])

然后我们可以实现cross-entropy函数 -sum (y’log(y))：

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

首先，tf.log计算每个元素的对数y。接下来，我们乘以每个元素y_与相应的元素tf.log(y)。然后tf.reduce_sum在y的第二维中添加元素，由于reduction_indices=[1]参数。最后，tf.reduce_mean计算批处理中所有示例的平均值。

请注意，在源代码中，我们不使用这个公式，因为它在数值上是不稳定的。相反，我们应用tf.nn.softmax_cross_entropy_with_logits在非规范化的logits(例如，我们在tf.matmul(x, W) + b上调用softmax_cross_entropy_with_logits)，因为这个在数值上更稳定的函数在内部计算softmax激活。在你的代码中，考虑使用tf.nn.softmax_cross_entropy_with_logits代替。

现在我们知道我们想要我们的模型做什么了，TensorFlow很容易训练它做到这一点。由于TensorFlow知道您的计算的整个图表，它可以自动使用反向传播算法有效地确定你的变量如何影响你所要求的最小损失。然后它可以应用你选择的优化算法来修改变量并减少损失。

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

在这种情况下，我们要求TensorFlow最小化cross_entropy，使用梯度下降算法，学习率为0.5。梯度下降是一个简单的过程，其中TensorFlow简单地将每个变量稍微向降低成本的方向移动一点。但是TensorFlow也提供了许多其他优化算法：使用任意一个就像调整一行代码那么简单。

TensorFlow在这个场景之下实际做的是：添加新的操作到你的图(其中实现了反向传播和梯度下降)。然后它给你一个单一的操作，运行时，做一步梯度下降训练，稍微调整你的变量，以减少损失。

我们现在可以启动模型了，使用InteractiveSession：

sess = tf.InteractiveSession()

我们首先必须创建一个操作来初始化我们创建的变量：

tf.global_variables_initializer().run()

接下来开始训练 – 我们将运行1000次的训练步骤！

for _ in range(1000):
  batch_xs, batch_ys = mnist.train.next_batch(100)
  sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

循环的每一步，从训练集中得到一百个随机数据点的”batch”。执行train_step，使用batch数据填充placeholder。

使用小批量的随机数据称为随机训练 – 在这种情况下，随机梯度下降。理想情况下，我们希望将所有数据用于每一步训练，因为这样可以让我们更好地了解我们应该做什么，但是这样做很耗时。所以，相反，我们每次都使用不同的子集。这样做很省时，而且有很多相同的好处。

评估我们的模型

我们的模型有多好？

首先让我们弄清楚我们预测了正确的标签。tf.argmax是一个非常有用的函数，它可以使您得到在张量中沿某个轴值最大的索引。例如，tf.argmax(y,1)是针对每个输入我们模型认为最有可能的标签，而tf.argmax(y_,1)是正确的标签。我们可以用tf.equal检查我们的预测是否符合事实。

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

这给了我们一个布尔的列表。为了确定什么分数是正确的，我们转换为浮点数，然后取平均值。例如，[True, False, True, True]会成为[1,0,1,1]这将成为0.75。

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

最后，我们计算在测试数据上的准确性。

print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

这应该是大约92％。

这个效果比较一般，因为我们正在使用一个非常简单的模型。做一些小的变化，我们可以达到97％。最好的模型可以达到超过99.7％的准确性！ (欲了解更多信息，请看看这个结果列表。)

重要的是我们从这个模型中学到了东西。不过，如果您对这些结果感到有些失望，请查看下一个教程我们做得更好，并学习如何使用TensorFlow建立更复杂的模型！