MNIST Tensorflow新手教程

本教程麵向剛學習機器學習和TensorFlow的讀者。如果您已經知道MNIST是什麽，以及softmax(多項式邏輯)回歸是什麽，那麽您可以跳到節奏更快的教程。在開始任何教程之前務必安裝TensorFlow。

當學習如何編程時，首先要做的就是打印“Hello World”。編程起步有Hello World，而機器學習起步就是MNIST。

MNIST是一個簡單的計算機視覺數據集。它由這樣的手寫數字的圖像組成：

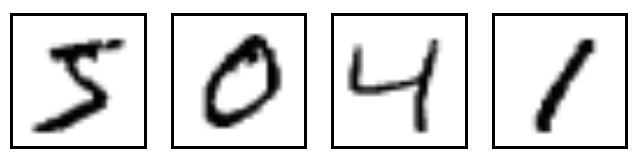
它還包括每個圖像的標簽，告訴我們它是哪個數字。例如，上述圖像的標簽是5,0,4和1。

在本教程中，我們將訓練一個模型來查看圖像並預測它們是什麽數字。我們的目標不是訓練一個能夠達到state-of-the-art表現的精心製作的模型 – 盡管我們稍後會給您提供代碼！ – 而是傾向於讓您學會TensorFlow的入門級用法。因此，我們將從一個非常簡單的模型開始，稱為Softmax回歸。

本教程的實際代碼非常短，所有有趣的東西都隻發生在三行中。然而，了解其背後的理念非常重要：TensorFlow的工作原理和核心機器學習概念。正因為如此，我們要非常小心的走查代碼。

關於本教程

這個教程是對這個文件一行一行的代碼解釋。

您可以通過幾種不同的方式使用本教程，其中包括：

• 閱讀每行的解釋時，將每個代碼段逐行複製並粘貼到Python環境中。
• 在閱讀解釋之前或之後，運行整個mnist_softmax.pyPython文件，並使用本教程來理解不清楚的代碼行。

我們將在本教程中完成的任務：

• 了解MNIST數據和softmax回歸
• 根據查看圖像中的每個像素，創建一個識別數字的模型
• 使用TensorFlow訓練模型，通過查看數千個示例來識別數字(並運行我們的第一個TensorFlow會話來完成)
• 用我們的測試數據檢查模型的準確性

MNIST數據

MNIST數據托管在Yann LeCun的網站。如果您正在複製和粘貼本教程中的代碼，請從這裏開始這兩行代碼，它們將自動下載並讀取數據：

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

MNIST數據分為三部分：55,000個訓練數據的數據點(mnist.train)，10000點的測試數據(mnist.test)和5,000點驗證數據(mnist.validation)。這種分裂是非常重要的：機器學習中必須具備我們不能從中學習的獨立數據，這樣我們才能確保我們學到的東西實際上可泛化的！

如前所述，每個MNIST數據點有兩部分：一個手寫數字的圖像和一個相應的標簽。我們將調用圖像”x”和標簽”y”。訓練集和測試集都包含圖像及其相應的標簽;例如訓練圖像是mnist.train.images和訓練標簽是mnist.train.labels。

每個圖像是28像素×28像素。我們可以把它解釋為一大堆數字：

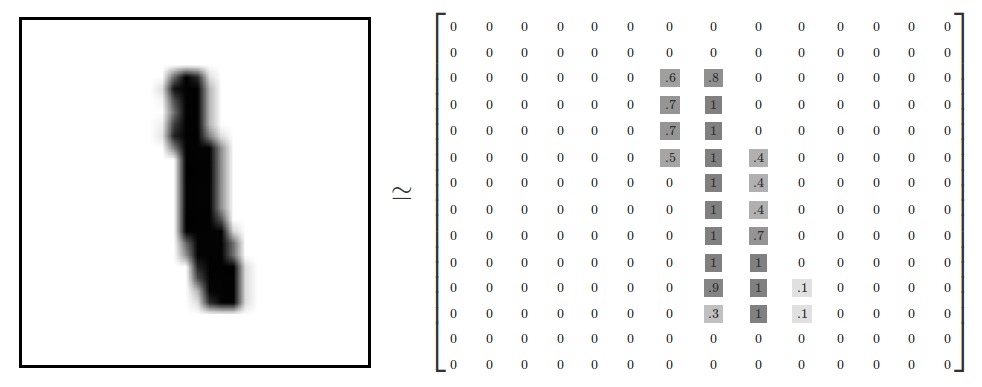
我們可以把這個數組變成一個28×28 = 784的數字。隻要我們在圖像之間保持一致，那麽我們如何展開陣列並不重要。從這個角度來看，MNIST圖像隻是784維向量空間中的一束點，結構非常豐富(警告：計算密集的可視化)。

展平數據會丟棄有關圖像二維結構的信息。這可能是有問題的，但是，最好的計算機視覺方法就是可以利用這個結構的，我們將在後麵的教程中介紹。在這裏隻使用的簡單方法，softmax回歸(下麵定義)。

結果就是這樣：mnist.train.images是一個張量(n-dimensional陣列)，形狀是[55000, 784]。第一維是圖像列表的索引，第二維是每個圖像中每個像素的索引。張量中的每個條目是針對特定圖像中的特定像素的介於0和1之間的像素強度。

MNIST中的每個圖像都有相應的標簽，0到9之間的數字代表圖像中繪製的數字。

為了本教程的目的，我們將要求我們的標簽為“one-hot vectors”。 one-hot向量是一個在大多數維度上為0，在一個維度上為1的向量。在這種情況下，第n個數字將被表示為在第n維中為1的向量。例如，3將是[0,0,0,1,0,0,0,0,0,0]。所以，mnist.train.labels是一個[55000, 10]浮點數陣列。

Softmax回歸

我們知道MNIST中的每個圖像都是一個0到9之間的手寫數字。所以一個給定的圖像可能隻有十個可能的東西。我們希望能夠看到一個圖像，並給出它是每個數字的概率。例如，我們的模型可能會查看一張9的圖片，並且有80％確定這是一張9的圖片，但是給出一個5％的概率是因為它是一個8(因為頂部循環)，並且對所有其他的概率有一點概率，這不是100％確定。

這是說明softmax回歸是一個自然，簡單模型的經典案例。如果你想把一個對象的概率分配給幾個不同的東西之一，softmax就是要做的事情，因為softmax給了我們一個0到1之間的數值列表，加起來就是1。後續，當我們訓練更複雜的模型，最後一步仍然會是一個softmax層。

softmax回歸有兩個步驟：首先我們將輸入的證據加在某些類別中，然後將證據轉換成概率。

為了收集給定圖像在特定類別中的證據，我們進行像素強度的加權總和。如果具有高強度的像素是針對在該類別中的圖像的證據，則權重是負的;如果證據是有利的，則權重是正的。

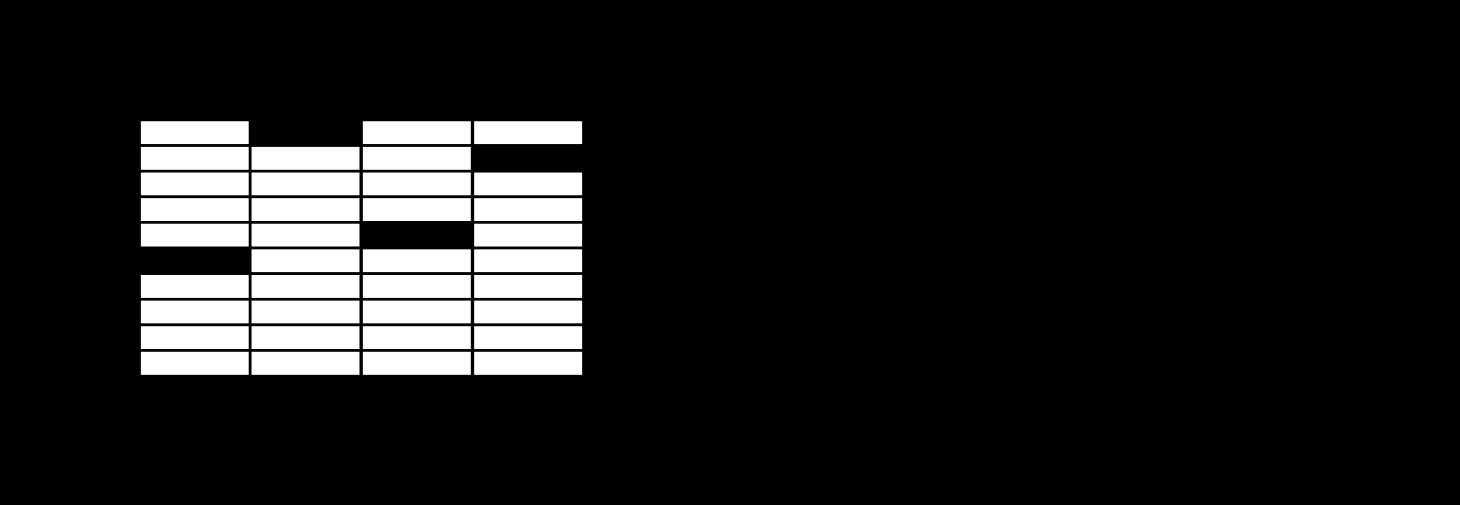
下圖顯示了一個模型為每個類學習的權重。紅色代表負麵權重，藍色代表正麵權重。

我們還添加了一些額外的證據，稱為偏置。基本上，我們希望能夠說有些東西更可能獨立於輸入。結果是給定輸入x的屬於類i的證據是：

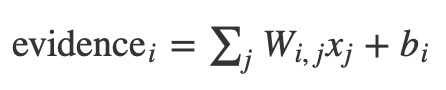
其中w_i是權重，b_i是類別i的偏差，j是對輸入圖像中的像素進行求和的索引。然後，我們使用”softmax”函數將證據符號轉換成我們的預測概率y：

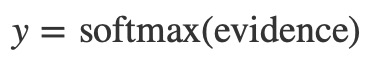
在這裏，softmax用作”activation”或”link”函數，將線性函數的輸出整形成我們想要的形式 – 在這種情況下，概率分布超過10種情況。你可以把它看作是將證據的轉換轉化為我們在每個類中投入的概率。它被定義為：

如果將這個等式展開，你會得到：

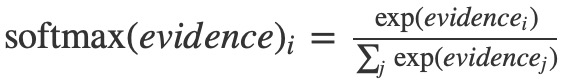
但是，按第一種方式考慮softmax是更有幫助的：指數化輸入，然後使其正則化。指數意味著多一個單位的證據增加了任何假設乘加的權重。而相反，少一個證據單位意味著一個假設獲得了早期權重的一小部分。沒有假設曾經有零或負權重。 Softmax然後歸一化這些權重，使它們加起來為1，形成有效的概率分布。 (為了得到關於softmax函數的更多知識，參考部分在邁克爾·尼爾森的書中，有一個互動的可視化。)

您可以將我們的softmax回歸看成如下所示，盡管有更多x。對於每個輸出，我們計算x的加權和，加一個偏差，然後應用softmax。

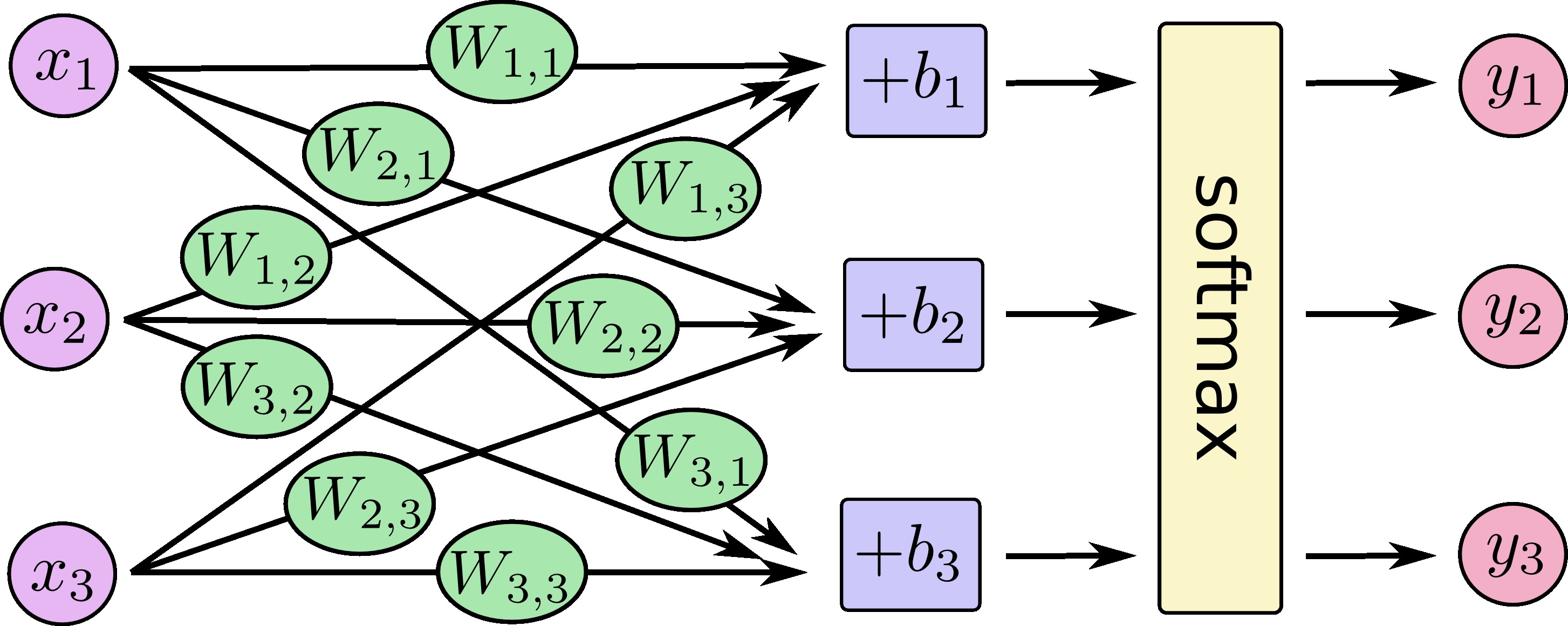
如果我們把它寫成等式，我們得到：

我們可以用”vectorize”這個程序，把它變成一個矩陣乘法和矢量加法，從而提升計算性能。

更簡潔，我們可以寫：

現在讓我們把它轉換成TensorFlow可以使用的東西。

實現回歸

為了在Python中進行高效的數值計算，我們通常使用NumPy一類的庫，在Python之外執行耗時的操作，例如矩陣乘法，使用以另一種語言實現的高效代碼。不幸的是，每一次操作都會返回到Python，這仍然會有很多開銷。如果要在GPU上運行計算或以分布式方式運行計算，則傳輸數據的成本更高，所以此開銷尤其糟糕。

TensorFlow也在Python之外進行繁重的工作，但是為了避免這種開銷，還需要進一步的工作。 TensorFlow不是獨立於Python運行一個昂貴的操作，而是讓我們描述一個完全在Python之外運行的交互操作圖。 (像這樣的方法也可以在其他幾個機器學習庫中看到)

要使用TensorFlow，首先我們需要導入它。

import tensorflow as tf

我們通過操縱符號變量來描述這些交互操作。我們來創建一個：

x = tf.placeholder(tf.float32, [None, 784])

x不是一個具體的值。它是placeholder，當我們要求TensorFlow運行一個計算時，我們將輸入一個值。我們希望能夠輸入任意數量的MNIST圖像，每個圖像被平麵化成784維向量。我們將其表示為floating-point數字的二維張量[None, 784]。 (這裏None意味著尺寸可以是任意長度。)

我們也需要我們的模型的權重和偏置。我們可以想象把這些看作是額外的投入，但TensorFlow有一個更好的方法來處理它：Variable。一個Variable是在TensorFlow的交互操作圖中的可修改的張量。它可以被使用，甚至被計算修改。對於機器學習應用，模型參數通常定義為Variable。

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

我們創造這些Variables，通過給予tf.Variable初始值的方式：在這種情況下，我們初始化W和b作為充滿零的張量。既然我們要學到W和b的理想值，它們最初的內容並不重要。

注意到W具有[784，10]的形狀，因為我們想通過乘以784維圖像向量來產生區分類別的證據的10維向量。b具有[10]的形狀，所以我們可以將其添加到輸出。

我們現在可以實現我們的模型。隻需要一行來定義它！

y = tf.nn.softmax(tf.matmul(x, W) + b)

首先，我們通過表達式tf.matmul(x, W)將x和W相乘。這是從方程中乘以它們的時候翻轉過來的，在那裏我們有了(Wx)，作為一個小技巧來處理x是具有多個輸入的2D張量。然後我們添加b，最後應用tf.nn.softmax。

就這麽簡單。經過幾行簡單的設置之後，我們隻用一行代碼來定義我們的模型。這並不是因為TensorFlow被設計成使得softmax回歸特別容易：從機器學習模型到物理模擬，這隻是描述多種數值計算的一種非常靈活的方式。一旦定義，我們的模型可以在不同的設備上運行：計算機的CPU，GPU甚至是手機！

訓練

為了訓練我們的模型，我們需要定義模型的好壞標準。實際上，在機器學習中，我們通常定義一個模型的壞處，我們稱之為成本或損失，它表示我們的模型離我們期望的結果有多遠。我們盡量減少這個誤差，誤差越小，我們的模型就越好。

一個非常常見損失函數被稱為”cross-entropy.” Cross-entropy產生於信息論中的信息壓縮代碼的思想，但它是從賭博到機器學習的很多領域，作為一個重要的想法。它被定義為：

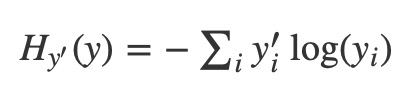
其中y是我們預測的概率分布，而y’是真正的分布(具有數字標簽的one-hot向量)。在一些粗略的意義上，cross-entropy正在測量我們的預測是如何低效的來描述真相。有關cross-entropy的更多細節超出了本教程的範圍，但它非常值得理解。

要實現cross-entropy，我們需要先添加一個新的占位符來輸入正確的答案：

y_ = tf.placeholder(tf.float32, [None, 10])

然後我們可以實現cross-entropy函數 -sum (y’log(y))：

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

首先，tf.log計算每個元素的對數y。接下來，我們乘以每個元素y_與相應的元素tf.log(y)。然後tf.reduce_sum在y的第二維中添加元素，由於reduction_indices=[1]參數。最後，tf.reduce_mean計算批處理中所有示例的平均值。

請注意，在源代碼中，我們不使用這個公式，因為它在數值上是不穩定的。相反，我們應用tf.nn.softmax_cross_entropy_with_logits在非規範化的logits(例如，我們在tf.matmul(x, W) + b上調用softmax_cross_entropy_with_logits)，因為這個在數值上更穩定的函數在內部計算softmax激活。在你的代碼中，考慮使用tf.nn.softmax_cross_entropy_with_logits代替。

現在我們知道我們想要我們的模型做什麽了，TensorFlow很容易訓練它做到這一點。由於TensorFlow知道您的計算的整個圖表，它可以自動使用反向傳播算法有效地確定你的變量如何影響你所要求的最小損失。然後它可以應用你選擇的優化算法來修改變量並減少損失。

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

在這種情況下，我們要求TensorFlow最小化cross_entropy，使用梯度下降算法，學習率為0.5。梯度下降是一個簡單的過程，其中TensorFlow簡單地將每個變量稍微向降低成本的方向移動一點。但是TensorFlow也提供了許多其他優化算法：使用任意一個就像調整一行代碼那麽簡單。

TensorFlow在這個場景之下實際做的是：添加新的操作到你的圖(其中實現了反向傳播和梯度下降)。然後它給你一個單一的操作，運行時，做一步梯度下降訓練，稍微調整你的變量，以減少損失。

我們現在可以啟動模型了，使用InteractiveSession：

sess = tf.InteractiveSession()

我們首先必須創建一個操作來初始化我們創建的變量：

tf.global_variables_initializer().run()

接下來開始訓練 – 我們將運行1000次的訓練步驟！

for _ in range(1000):
  batch_xs, batch_ys = mnist.train.next_batch(100)
  sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

循環的每一步，從訓練集中得到一百個隨機數據點的”batch”。執行train_step，使用batch數據填充placeholder。

使用小批量的隨機數據稱為隨機訓練 – 在這種情況下，隨機梯度下降。理想情況下，我們希望將所有數據用於每一步訓練，因為這樣可以讓我們更好地了解我們應該做什麽，但是這樣做很耗時。所以，相反，我們每次都使用不同的子集。這樣做很省時，而且有很多相同的好處。

評估我們的模型

我們的模型有多好？

首先讓我們弄清楚我們預測了正確的標簽。tf.argmax是一個非常有用的函數，它可以使您得到在張量中沿某個軸值最大的索引。例如，tf.argmax(y,1)是針對每個輸入我們模型認為最有可能的標簽，而tf.argmax(y_,1)是正確的標簽。我們可以用tf.equal檢查我們的預測是否符合事實。

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

這給了我們一個布爾的列表。為了確定什麽分數是正確的，我們轉換為浮點數，然後取平均值。例如，[True, False, True, True]會成為[1,0,1,1]這將成為0.75。

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

最後，我們計算在測試數據上的準確性。

print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

這應該是大約92％。

這個效果比較一般，因為我們正在使用一個非常簡單的模型。做一些小的變化，我們可以達到97％。最好的模型可以達到超過99.7％的準確性！ (欲了解更多信息，請看看這個結果列表。)

重要的是我們從這個模型中學到了東西。不過，如果您對這些結果感到有些失望，請查看下一個教程我們做得更好，並學習如何使用TensorFlow建立更複雜的模型！