使用TensorFlow進行股票價格預測的簡單深度學習模型
我們最近在做一個黑客馬拉鬆STATWORX,一些團隊成員從穀歌金融API那裏獲得了詳細的標普500指數數據。數據包括指數以及標準普爾500指數成分股的股價。掌握這些數據後,我想開發一種基於500個成分股價格預測標準普爾500指數的深度學習模型。
使用TensorFlow處理數據和構建深度學習模型非常有趣,因此我決定編寫:一個關於預測S& P 500股票價格的小型TensorFlow教程。您將閱讀的內容不是深度教程,更多的是從高層次介紹TensorFlow模型的重要模塊和概念。我創建的Python代碼沒有針對效率和可理解性進行優化。已經使用的數據集可以從這裏(40MB)下載。
導入和準備數據
我們將抓取服務器中的庫存數據作為csv文件導出。數據集包含n = 41266條有關500隻股票的2017年4月至8月數據以及標準普爾500指數總價的分鍾數據。
# Import data
data = pd.read_csv('data_stocks.csv')# Drop date variable data = data.drop(['DATE'], 1)
# Dimensions of dataset
n = data.shape[0]
p = data.shape[1]# Make data a numpy array data = data.values
數據已經做預處理被,這意味著缺少庫存和指數價格(LOCF’ed)(最後一次觀察結轉),以便該文件不包含任何缺失值。
快速查看S& P時間序列的使用情況:pyplot.plot(data['SP500']):
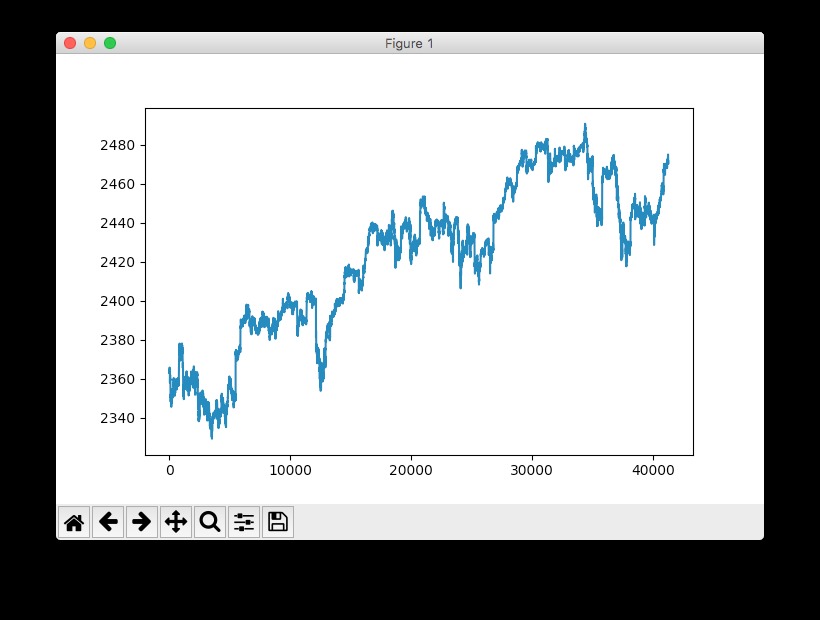
注:這實際上是標準普爾500指數的提前,也就是說,其具體指向未來做了1分鍾的轉移。這個操作是必要的,因為我們要預測下一分鍾的指數而不是當前分鍾。
準備訓練和測試數據
數據集被分成訓練和測試數據。訓練數據包含總數據集的80%。數據不是洗牌,而是依次切片。訓練數據範圍從四月到大約。 2017年7月底,測試數據將於2017年8月底結束。
# Training and test data
train_start = 0
train_end = int(np.floor(0.8*n))
test_start = train_end
test_end = n
data_train = data[np.arange(train_start, train_end), :]
data_test = data[np.arange(test_start, test_end), :]時間序列交叉驗證有很多不同的方法,比如有或沒有改動的滾動預測或更複雜的概念,如時間序列自舉重采樣。後者涉及時間序列的其餘季節性分解的重複樣本,以模擬遵循與原始時間序列相同的季節性模式但不是其值的精確副本的樣本。
數據縮放
大多數神經網絡體係結構從縮放輸入(有時也是輸出)中獲益。為什麽?因為網絡的神經元如tanh或sigmoid的大多數常見的激活功能定義在[-1, 1]或者[0, 1]區間。目前,整流線性單元(ReLU)激活是常用的激活函數,其在可能激活值的軸上是無界的。但是,無論如何,我們都會調整輸入和目標。使用sklearn的MinMaxScaler可以輕鬆地在Python中完成縮放。
# Scale data
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(data_train)
data_train = scaler.transform(data_train)
data_test = scaler.transform(data_test)# Build X and y
X_train = data_train[:, 1:]
y_train = data_train[:, 0]
X_test = data_test[:, 1:]
y_test = data_test[:, 0]注意:必須小心謹慎哪部分數據在什麽時候應該被縮放。一個常見的錯誤是在訓練集和測試集拆分應用之前縮放整個數據集。為什麽這是一個錯誤?由於縮放調用統計量,例如變量的最小/最大值。在現實生活中執行時間序列預測時,在預測時您沒有來自未來觀測的信息。因此,必須對訓練數據進行比例統計計算,然後將其應用於測試數據。否則,您在預測時使用未來信息,這往往會使預測指標偏向正向。
TensorFlow簡介
TensorFlow是一款強大的軟件,目前是領先的深度學習和神經網絡計算框架。它基於C++底層後端,但通常通過Python控製(也有一個整潔R的TensorFlow庫,由RStudio維護)。 TensorFlow基於計算任務的圖形表示進行操作。這種方法允許用戶將數學運算指定為數據,變量和運算符是圖中的元素。由於神經網絡實際上是數據和數學運算的圖形,因此TensorFlow僅適用於神經網絡和深度學習。看看這個簡單的例子:
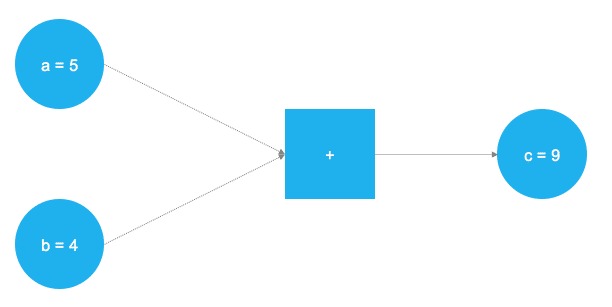
在上圖中,應該添加兩個數字。這些數字存儲在兩個變量中,a和b。這兩個值流經圖表並到達正方形節點,在那裏添加它們。加法的結果存儲在另一個變量中,c。其實,a,b和c可以被視為占位符。任何被輸入的數字a和b獲得添加並存儲到c。這正是TensorFlow的工作原理。用戶通過占位符和變量定義模型(神經網絡)的抽象表示。之後,占位符將獲得填充”filled”實際數據並進行實際計算。以下代碼在TensorFlow中實現了上麵的玩具示例:
# Import TensorFlow
import tensorflow as tf# Define a and b as placeholders
a = tf.placeholder(dtype=tf.int8)
b = tf.placeholder(dtype=tf.int8)
# Define the addition
c = tf.add(a, b)
# Initialize the graph
graph = tf.Session()
# Run the graph
graph.run(c, feed_dict={a: 5, b: 4})
導入TensorFlow庫之後,定義了兩個占位符tf.placeholder()。它們對應於上圖中左側的兩個藍色圓圈。之後,通過定義數學加法tf.add()。計算的結果是c = 9。使用占位符設置,可以使用任何a和b整數值執行圖形。當然,前一個問題隻是一個玩具的例子。神經網絡中所需的圖形和計算要複雜得多。
占位符
如前所述,這一切都始於占位符。我們需要兩個占位符才能符合我們的模型:X包含網絡的投入(當時所有標準普爾500指數成分股的股價,在T = t)和Y網絡的輸出(標準普爾500指數值,在T = t + 1)。
占位符的形狀對應於[None, n_stocks]同[None]這意味著輸入是二維矩陣,輸出是一維矢量。了解神經網絡需要哪些輸入和輸出尺寸才能正確設計,這是至關重要的。
# Placeholder
X = tf.placeholder(dtype=tf.float32, shape=[None, n_stocks])
Y = tf.placeholder(dtype=tf.float32, shape=[None])該None參數表明在這一點上,我們還不知道在每批中流過神經網絡圖的觀測值的數量,所以我們保持靈活性。我們稍後將定義該變量batch_size,它控製每個訓練批次的觀察次數。
變量
除了占位符,變量是TensorFlow世界的另一個基石。盡管占位符用於在圖中存儲輸入數據和目標數據,但變量在圖形內用作靈活容器,在圖形執行期間允許更改。權重和偏差被表示為變量以便在訓練期間擬合。變量需要在模型訓練之前進行初始化。我們稍後會詳細討論這個問題。
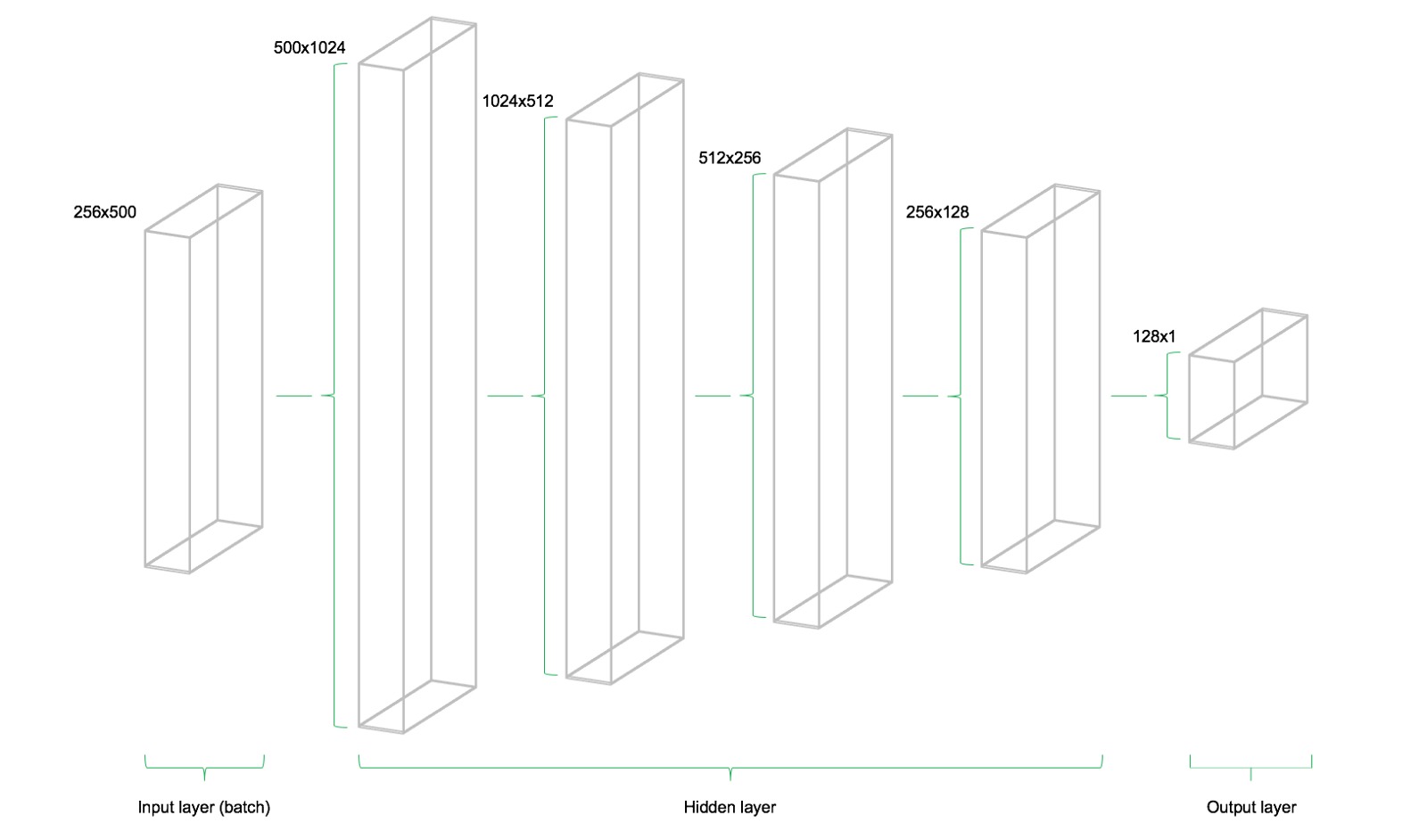
該模型由四個隱藏層組成。第一層包含1024個神經元,略大於輸入大小的兩倍。隨後的隱藏層總是上一層的一半,這意味著512,256和最後128個神經元。減少每個後續圖層的神經元數量會壓縮網絡在前麵圖層中識別的信息。當然,其他網絡體係結構和神經元配置也是可能的,但不在此介紹級文章的範圍內。
# Model architecture parameters n_stocks = 500 n_neurons_1 = 1024 n_neurons_2 = 512 n_neurons_3 = 256 n_neurons_4 = 128 n_target = 1
# Layer 1: Variables for hidden weights and biases
W_hidden_1 = tf.Variable(weight_initializer([n_stocks, n_neurons_1]))
bias_hidden_1 = tf.Variable(bias_initializer([n_neurons_1]))# Layer 2: Variables for hidden weights and biases
W_hidden_2 = tf.Variable(weight_initializer([n_neurons_1, n_neurons_2]))
bias_hidden_2 = tf.Variable(bias_initializer([n_neurons_2]))# Layer 3: Variables for hidden weights and biases
W_hidden_3 = tf.Variable(weight_initializer([n_neurons_2, n_neurons_3]))
bias_hidden_3 = tf.Variable(bias_initializer([n_neurons_3]))# Layer 4: Variables for hidden weights and biases
W_hidden_4 = tf.Variable(weight_initializer([n_neurons_3, n_neurons_4]))
bias_hidden_4 = tf.Variable(bias_initializer([n_neurons_4]))# Output layer: Variables for output weights and biases
W_out = tf.Variable(weight_initializer([n_neurons_4, n_target]))
bias_out = tf.Variable(bias_initializer([n_target]))
了解輸入層,隱藏層和輸出層之間所需的變量尺寸非常重要。作為多層感知器(MLP,這裏使用的網絡類型)的一個經驗法則,前一層的第二維是當前層中權重矩陣的第一維。這可能聽起來很複雜,但實質上隻是每個圖層都將其輸出作為輸入傳遞到下一圖層。偏差維度等於當前圖層的權重矩陣的第二維度,其對應於該層中的神經元的數量。
設計網絡體係結構
在定義所需的權重和偏置變量後,需要指定網絡拓撲結構和網絡結構。因此,占位符(數據)和變量(權重和偏置)需要組合成一個連續矩陣乘法係統。
此外,網絡的隱藏層被激活函數轉換。激活函數是網絡體係結構的重要組成部分,因為它們將非線性引入到係統中。有幾十種可能的激活功能,其中最常見的是整流線性單元(ReLU),它也將用於此模型。
# Hidden layer
hidden_1 = tf.nn.relu(tf.add(tf.matmul(X, W_hidden_1), bias_hidden_1))
hidden_2 = tf.nn.relu(tf.add(tf.matmul(hidden_1, W_hidden_2), bias_hidden_2))
hidden_3 = tf.nn.relu(tf.add(tf.matmul(hidden_2, W_hidden_3), bias_hidden_3))
hidden_4 = tf.nn.relu(tf.add(tf.matmul(hidden_3, W_hidden_4), bias_hidden_4))# Output layer (must be transposed)
out = tf.transpose(tf.add(tf.matmul(hidden_4, W_out), bias_out))
下圖展示了網絡架構。該模型由三個主要構件組成。輸入層,隱藏層和輸出層。這種架構被稱為前饋網絡。前饋表示該批數據僅從左向右流動。其他網絡體係結構(例如遞歸神經網絡)也允許數據在網絡中反向“backwards”傳輸。
損失函數(成本函數)
網絡的成本函數用於生成網絡預測與實際觀察到的訓練目標之間的偏差度量。對於回歸問題,通常使用均方誤差(MSE)函數。 MSE計算預測和目標之間的平均方差。基本上,可以執行任何可微函數來計算預測和目標之間的偏差度量。
# Cost function
mse = tf.reduce_mean(tf.squared_difference(out, Y))然而,MSE展現出對於要解決的一般優化問題有利的某些性質。
優化
優化器負責在訓練期間用於調整網絡的權重和偏置變量的必要計算。這些計算調用了所謂梯度的計算,這些計算表明訓練期間權重和偏置必須改變的方向,以最小化網絡的成本函數。穩定快速的優化器的開發是神經網絡的一個重要領域,也是一項深度學習研究。
# Optimizer
opt = tf.train.AdamOptimizer().minimize(mse)這裏使用了Adam Optimizer,它是深度學習開發中當前默認的優化器之一。Adam代表“Adaptive Moment Estimation”,可以被視為兩個其他流行優化器AdaGrad和RMSProp的組合。
初始化器
初始化器用於在訓練之前初始化網絡的變量。由於神經網絡是使用數值優化技術進行訓練的,所以優化問題的出發點是找到潛在問題的良好解決方案的關鍵因素之一。 TensorFlow中有不同的初始化程序,每種初始化程序都有不同的初始化方法。在這裏,我使用tf.variance_scaling_initializer(),這是默認的初始化策略之一。
# Initializers
sigma = 1
weight_initializer = tf.variance_scaling_initializer(mode="fan_avg", distribution="uniform", scale=sigma)
bias_initializer = tf.zeros_initializer()請注意,使用TensorFlow可以為圖中的不同變量定義多個初始化函數。但是,在大多數情況下,統一初始化就足夠了。
擬合神經網絡
在定義了網絡的占位符,變量,初始化器,成本函數和優化器之後,需要對模型進行訓練。通常,這是通過小批量訓練完成的。在小批次訓練期間隨機數據樣本n = batch_size從訓練數據中提取出來並饋入網絡。訓練數據集被分成n / batch_size依次饋入網絡的批次。此時占位符X和Y參加進來。它們存儲輸入和目標數據,並將它們作為輸入和目標呈現給網絡。
一批抽樣數據X流過網絡直到它到達輸出層。在那裏,TensorFlow將模型預測與實際觀察到的目標Y在當前批次中進行比較。之後,TensorFlow執行優化步驟並更新與所選學習方案相對應的網絡參數。在更新權重和偏置之後,下一個批次被采樣並且該過程重複執行。該過程將繼續,直到所有批次都已呈現給網絡。對所有數據進行一次全麵掃描被稱為一個epoch。
一旦達到了最大數量的epochs或用戶定義的另一個停止標準,網絡的訓練就會停止。
# Make Session net = tf.Session()
# Run initializer
net.run(tf.global_variables_initializer())# Setup interactive plot
plt.ion()
fig = plt.figure()
ax1 = fig.add_subplot(111)
line1, = ax1.plot(y_test)
line2, = ax1.plot(y_test*0.5)
plt.show()
# Number of epochs and batch size
epochs = 10
batch_size = 256
# Shuffle training data
shuffle_indices = np.random.permutation(np.arange(len(y_train)))
X_train = X_train[shuffle_indices]
y_train = y_train[shuffle_indices]
# Minibatch training
for i in range(0, len(y_train) // batch_size):
start = i * batch_size
batch_x = X_train[start:start + batch_size]
batch_y = y_train[start:start + batch_size]
# Run optimizer with batch
net.run(opt, feed_dict={X: batch_x, Y: batch_y})
# Show progress
if np.mod(i, 5) == 0:
# Prediction
pred = net.run(out, feed_dict={X: X_test})
line2.set_ydata(pred)
plt.title(‘Epoch ‘ + str(e) + ‘, Batch ‘ + str(i))
file_name = ‘img/epoch_’ + str(e) + ‘_batch_’ + str(i) + ‘.jpg’
plt.savefig(file_name)
plt.pause(0.01)
# Print final MSE after Training
mse_final = net.run(mse, feed_dict={X: X_test, Y: y_test})
print(mse_final)
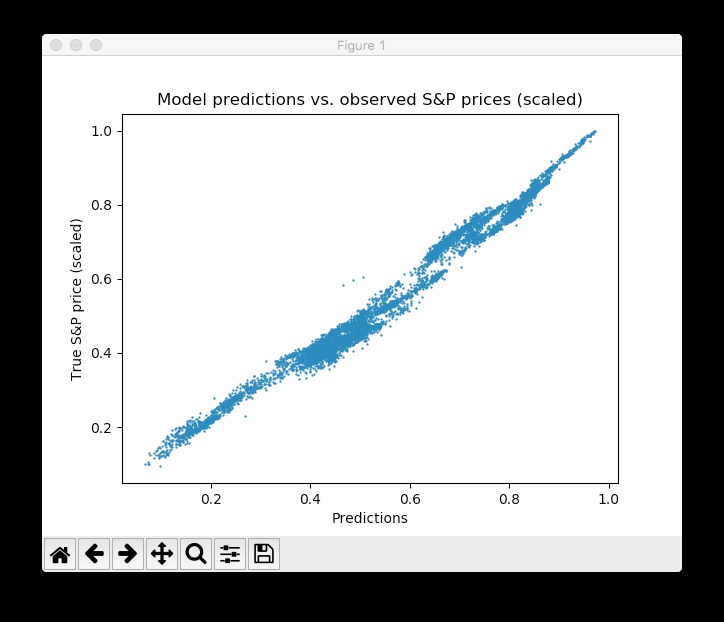
在訓練過程中,我們評估測試集上的網絡預測數據 – 這些數據不是跟學習無關,而是額外保留的 – 每5批次進行一次可視化。此外,圖像被導出到磁盤,然後組合成訓練過程的視頻動畫(見下文)。該模型可以快速了解測試數據中時間序列的形狀和位置,並能夠在幾輪epochs後產生準確的預測結果。太好了!
人們可以看到,網絡很快適應時間序列的基本形狀,並繼續學習更精細的數據模式。這也對應於在模型訓練期間降低學習速率的Adam學習方案,以便不超過優化最小值。經過10個epochs後,我們與測試數據非常接近!最終的測試MSE等於0.00078(這是非常低的,因為目標是縮放的)。測試集預測的平均絕對百分比誤差等於5.31%,這相當不錯。請注意,這僅適用於測試數據,實際情況下沒有實際的樣本量度。
請注意,有很多方法可以進一步改善這一結果:設計圖層和神經元,選擇不同的初始化和激活方案,引入神經元丟失層,提前停止等等。此外,不同類型的深度學習模型(如遞歸神經網絡)可能會在此任務中獲得更好的性能。但是,這不是這篇介紹性文章的範圍。
結論和展望
TensorFlow的發布是深度學習研究中的一個裏程碑事件。其靈活性和性能使研究人員能夠開發各種複雜的神經網絡體係結構以及其他ML算法。然而,與較高級別的API相比,靈活性的代價是更長的time-to-model周期,例如Keras或MxNet。盡管如此,我確信TensorFlow將在神經網絡和深入學習的研究和實際應用開發中走向de-facto標準。我們的許多客戶已經在使用TensorFlow或開始開發使用TensorFlow模型的項目。我們的數據科學顧問在STATWORX大量使用TensorFlow進行深度學習和神經網絡研究與開發。讓我們看看Google為TensorFlow的未來計劃了什麽。至少在我看來,缺少的一件事是用TensorFlow後端設計和開發神經網絡體係結構的整潔的圖形用戶界麵。也許,這是Google正在處理的內容;)
更新:我已經將Python腳本和(壓縮)數據集都添加到了一個Github存儲庫。請隨意克隆和分支。
