使用TensorFlow进行股票价格预测的简单深度学习模型
我们最近在做一个黑客马拉松STATWORX,一些团队成员从谷歌金融API那里获得了详细的标普500指数数据。数据包括指数以及标准普尔500指数成分股的股价。掌握这些数据后,我想开发一种基于500个成分股价格预测标准普尔500指数的深度学习模型。
使用TensorFlow处理数据和构建深度学习模型非常有趣,因此我决定编写:一个关于预测S& P 500股票价格的小型TensorFlow教程。您将阅读的内容不是深度教程,更多的是从高层次介绍TensorFlow模型的重要模块和概念。我创建的Python代码没有针对效率和可理解性进行优化。已经使用的数据集可以从这里(40MB)下载。
导入和准备数据
我们将抓取服务器中的库存数据作为csv文件导出。数据集包含n = 41266条有关500只股票的2017年4月至8月数据以及标准普尔500指数总价的分钟数据。
# Import data
data = pd.read_csv('data_stocks.csv')# Drop date variable data = data.drop(['DATE'], 1)
# Dimensions of dataset
n = data.shape[0]
p = data.shape[1]# Make data a numpy array data = data.values
数据已经做预处理被,这意味着缺少库存和指数价格(LOCF’ed)(最后一次观察结转),以便该文件不包含任何缺失值。
快速查看S& P时间序列的使用情况:pyplot.plot(data['SP500']):
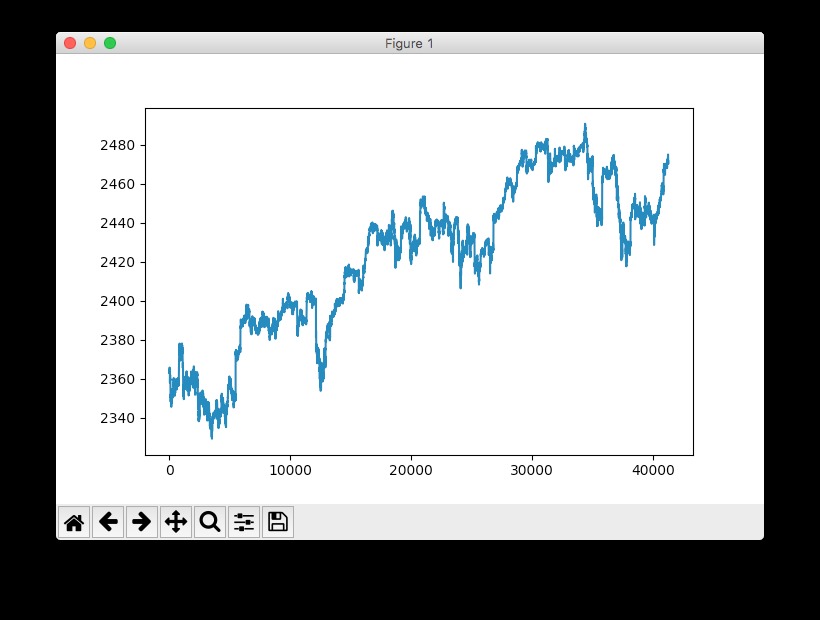
注:这实际上是标准普尔500指数的提前,也就是说,其具体指向未来做了1分钟的转移。这个操作是必要的,因为我们要预测下一分钟的指数而不是当前分钟。
准备训练和测试数据
数据集被分成训练和测试数据。训练数据包含总数据集的80%。数据不是洗牌,而是依次切片。训练数据范围从四月到大约。 2017年7月底,测试数据将于2017年8月底结束。
# Training and test data
train_start = 0
train_end = int(np.floor(0.8*n))
test_start = train_end
test_end = n
data_train = data[np.arange(train_start, train_end), :]
data_test = data[np.arange(test_start, test_end), :]时间序列交叉验证有很多不同的方法,比如有或没有改动的滚动预测或更复杂的概念,如时间序列自举重采样。后者涉及时间序列的其余季节性分解的重复样本,以模拟遵循与原始时间序列相同的季节性模式但不是其值的精确副本的样本。
数据缩放
大多数神经网络体系结构从缩放输入(有时也是输出)中获益。为什么?因为网络的神经元如tanh或sigmoid的大多数常见的激活功能定义在[-1, 1]或者[0, 1]区间。目前,整流线性单元(ReLU)激活是常用的激活函数,其在可能激活值的轴上是无界的。但是,无论如何,我们都会调整输入和目标。使用sklearn的MinMaxScaler可以轻松地在Python中完成缩放。
# Scale data
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(data_train)
data_train = scaler.transform(data_train)
data_test = scaler.transform(data_test)# Build X and y
X_train = data_train[:, 1:]
y_train = data_train[:, 0]
X_test = data_test[:, 1:]
y_test = data_test[:, 0]注意:必须小心谨慎哪部分数据在什么时候应该被缩放。一个常见的错误是在训练集和测试集拆分应用之前缩放整个数据集。为什么这是一个错误?由于缩放调用统计量,例如变量的最小/最大值。在现实生活中执行时间序列预测时,在预测时您没有来自未来观测的信息。因此,必须对训练数据进行比例统计计算,然后将其应用于测试数据。否则,您在预测时使用未来信息,这往往会使预测指标偏向正向。
TensorFlow简介
TensorFlow是一款强大的软件,目前是领先的深度学习和神经网络计算框架。它基于C++底层后端,但通常通过Python控制(也有一个整洁R的TensorFlow库,由RStudio维护)。 TensorFlow基于计算任务的图形表示进行操作。这种方法允许用户将数学运算指定为数据,变量和运算符是图中的元素。由于神经网络实际上是数据和数学运算的图形,因此TensorFlow仅适用于神经网络和深度学习。看看这个简单的例子:
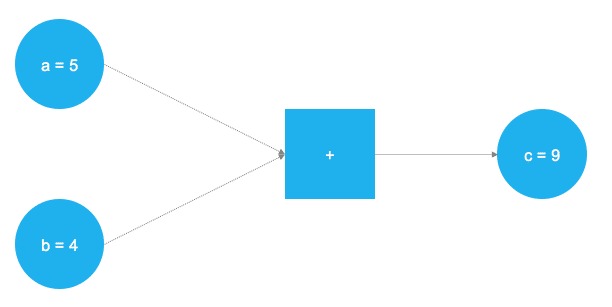
在上图中,应该添加两个数字。这些数字存储在两个变量中,a和b。这两个值流经图表并到达正方形节点,在那里添加它们。加法的结果存储在另一个变量中,c。其实,a,b和c可以被视为占位符。任何被输入的数字a和b获得添加并存储到c。这正是TensorFlow的工作原理。用户通过占位符和变量定义模型(神经网络)的抽象表示。之后,占位符将获得填充”filled”实际数据并进行实际计算。以下代码在TensorFlow中实现了上面的玩具示例:
# Import TensorFlow
import tensorflow as tf# Define a and b as placeholders
a = tf.placeholder(dtype=tf.int8)
b = tf.placeholder(dtype=tf.int8)
# Define the addition
c = tf.add(a, b)
# Initialize the graph
graph = tf.Session()
# Run the graph
graph.run(c, feed_dict={a: 5, b: 4})
导入TensorFlow库之后,定义了两个占位符tf.placeholder()。它们对应于上图中左侧的两个蓝色圆圈。之后,通过定义数学加法tf.add()。计算的结果是c = 9。使用占位符设置,可以使用任何a和b整数值执行图形。当然,前一个问题只是一个玩具的例子。神经网络中所需的图形和计算要复杂得多。
占位符
如前所述,这一切都始于占位符。我们需要两个占位符才能符合我们的模型:X包含网络的投入(当时所有标准普尔500指数成分股的股价,在T = t)和Y网络的输出(标准普尔500指数值,在T = t + 1)。
占位符的形状对应于[None, n_stocks]同[None]这意味着输入是二维矩阵,输出是一维矢量。了解神经网络需要哪些输入和输出尺寸才能正确设计,这是至关重要的。
# Placeholder
X = tf.placeholder(dtype=tf.float32, shape=[None, n_stocks])
Y = tf.placeholder(dtype=tf.float32, shape=[None])该None参数表明在这一点上,我们还不知道在每批中流过神经网络图的观测值的数量,所以我们保持灵活性。我们稍后将定义该变量batch_size,它控制每个训练批次的观察次数。
变量
除了占位符,变量是TensorFlow世界的另一个基石。尽管占位符用于在图中存储输入数据和目标数据,但变量在图形内用作灵活容器,在图形执行期间允许更改。权重和偏差被表示为变量以便在训练期间拟合。变量需要在模型训练之前进行初始化。我们稍后会详细讨论这个问题。
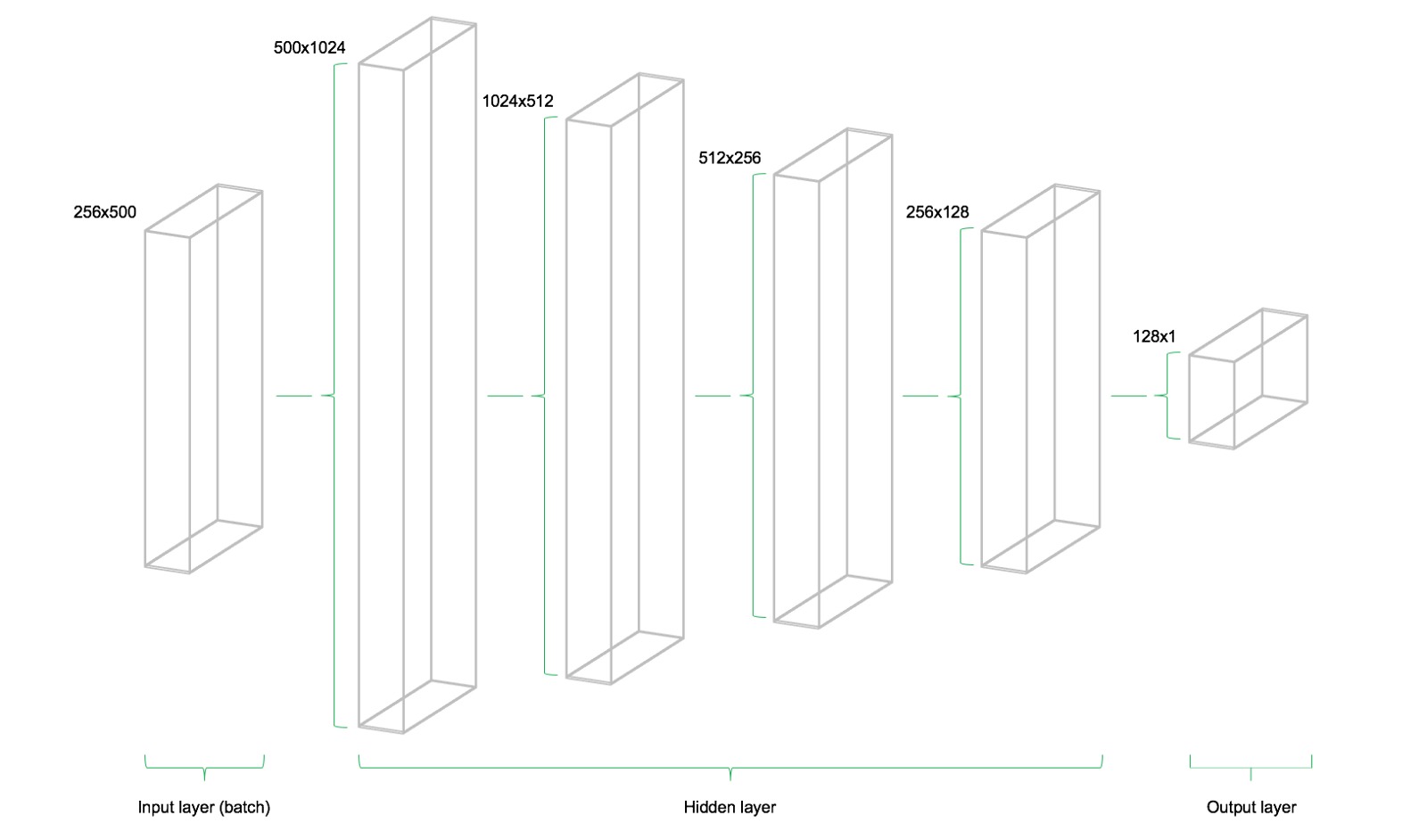
该模型由四个隐藏层组成。第一层包含1024个神经元,略大于输入大小的两倍。随后的隐藏层总是上一层的一半,这意味着512,256和最后128个神经元。减少每个后续图层的神经元数量会压缩网络在前面图层中识别的信息。当然,其他网络体系结构和神经元配置也是可能的,但不在此介绍级文章的范围内。
# Model architecture parameters n_stocks = 500 n_neurons_1 = 1024 n_neurons_2 = 512 n_neurons_3 = 256 n_neurons_4 = 128 n_target = 1
# Layer 1: Variables for hidden weights and biases
W_hidden_1 = tf.Variable(weight_initializer([n_stocks, n_neurons_1]))
bias_hidden_1 = tf.Variable(bias_initializer([n_neurons_1]))# Layer 2: Variables for hidden weights and biases
W_hidden_2 = tf.Variable(weight_initializer([n_neurons_1, n_neurons_2]))
bias_hidden_2 = tf.Variable(bias_initializer([n_neurons_2]))# Layer 3: Variables for hidden weights and biases
W_hidden_3 = tf.Variable(weight_initializer([n_neurons_2, n_neurons_3]))
bias_hidden_3 = tf.Variable(bias_initializer([n_neurons_3]))# Layer 4: Variables for hidden weights and biases
W_hidden_4 = tf.Variable(weight_initializer([n_neurons_3, n_neurons_4]))
bias_hidden_4 = tf.Variable(bias_initializer([n_neurons_4]))# Output layer: Variables for output weights and biases
W_out = tf.Variable(weight_initializer([n_neurons_4, n_target]))
bias_out = tf.Variable(bias_initializer([n_target]))
了解输入层,隐藏层和输出层之间所需的变量尺寸非常重要。作为多层感知器(MLP,这里使用的网络类型)的一个经验法则,前一层的第二维是当前层中权重矩阵的第一维。这可能听起来很复杂,但实质上只是每个图层都将其输出作为输入传递到下一图层。偏差维度等于当前图层的权重矩阵的第二维度,其对应于该层中的神经元的数量。
设计网络体系结构
在定义所需的权重和偏置变量后,需要指定网络拓扑结构和网络结构。因此,占位符(数据)和变量(权重和偏置)需要组合成一个连续矩阵乘法系统。
此外,网络的隐藏层被激活函数转换。激活函数是网络体系结构的重要组成部分,因为它们将非线性引入到系统中。有几十种可能的激活功能,其中最常见的是整流线性单元(ReLU),它也将用于此模型。
# Hidden layer
hidden_1 = tf.nn.relu(tf.add(tf.matmul(X, W_hidden_1), bias_hidden_1))
hidden_2 = tf.nn.relu(tf.add(tf.matmul(hidden_1, W_hidden_2), bias_hidden_2))
hidden_3 = tf.nn.relu(tf.add(tf.matmul(hidden_2, W_hidden_3), bias_hidden_3))
hidden_4 = tf.nn.relu(tf.add(tf.matmul(hidden_3, W_hidden_4), bias_hidden_4))# Output layer (must be transposed)
out = tf.transpose(tf.add(tf.matmul(hidden_4, W_out), bias_out))
下图展示了网络架构。该模型由三个主要构件组成。输入层,隐藏层和输出层。这种架构被称为前馈网络。前馈表示该批数据仅从左向右流动。其他网络体系结构(例如递归神经网络)也允许数据在网络中反向“backwards”传输。
损失函数(成本函数)
网络的成本函数用于生成网络预测与实际观察到的训练目标之间的偏差度量。对于回归问题,通常使用均方误差(MSE)函数。 MSE计算预测和目标之间的平均方差。基本上,可以执行任何可微函数来计算预测和目标之间的偏差度量。
# Cost function
mse = tf.reduce_mean(tf.squared_difference(out, Y))然而,MSE展现出对于要解决的一般优化问题有利的某些性质。
优化
优化器负责在训练期间用于调整网络的权重和偏置变量的必要计算。这些计算调用了所谓梯度的计算,这些计算表明训练期间权重和偏置必须改变的方向,以最小化网络的成本函数。稳定快速的优化器的开发是神经网络的一个重要领域,也是一项深度学习研究。
# Optimizer
opt = tf.train.AdamOptimizer().minimize(mse)这里使用了Adam Optimizer,它是深度学习开发中当前默认的优化器之一。Adam代表“Adaptive Moment Estimation”,可以被视为两个其他流行优化器AdaGrad和RMSProp的组合。
初始化器
初始化器用于在训练之前初始化网络的变量。由于神经网络是使用数值优化技术进行训练的,所以优化问题的出发点是找到潜在问题的良好解决方案的关键因素之一。 TensorFlow中有不同的初始化程序,每种初始化程序都有不同的初始化方法。在这里,我使用tf.variance_scaling_initializer(),这是默认的初始化策略之一。
# Initializers
sigma = 1
weight_initializer = tf.variance_scaling_initializer(mode="fan_avg", distribution="uniform", scale=sigma)
bias_initializer = tf.zeros_initializer()请注意,使用TensorFlow可以为图中的不同变量定义多个初始化函数。但是,在大多数情况下,统一初始化就足够了。
拟合神经网络
在定义了网络的占位符,变量,初始化器,成本函数和优化器之后,需要对模型进行训练。通常,这是通过小批量训练完成的。在小批次训练期间随机数据样本n = batch_size从训练数据中提取出来并馈入网络。训练数据集被分成n / batch_size依次馈入网络的批次。此时占位符X和Y参加进来。它们存储输入和目标数据,并将它们作为输入和目标呈现给网络。
一批抽样数据X流过网络直到它到达输出层。在那里,TensorFlow将模型预测与实际观察到的目标Y在当前批次中进行比较。之后,TensorFlow执行优化步骤并更新与所选学习方案相对应的网络参数。在更新权重和偏置之后,下一个批次被采样并且该过程重复执行。该过程将继续,直到所有批次都已呈现给网络。对所有数据进行一次全面扫描被称为一个epoch。
一旦达到了最大数量的epochs或用户定义的另一个停止标准,网络的训练就会停止。
# Make Session net = tf.Session()
# Run initializer
net.run(tf.global_variables_initializer())# Setup interactive plot
plt.ion()
fig = plt.figure()
ax1 = fig.add_subplot(111)
line1, = ax1.plot(y_test)
line2, = ax1.plot(y_test*0.5)
plt.show()
# Number of epochs and batch size
epochs = 10
batch_size = 256
# Shuffle training data
shuffle_indices = np.random.permutation(np.arange(len(y_train)))
X_train = X_train[shuffle_indices]
y_train = y_train[shuffle_indices]
# Minibatch training
for i in range(0, len(y_train) // batch_size):
start = i * batch_size
batch_x = X_train[start:start + batch_size]
batch_y = y_train[start:start + batch_size]
# Run optimizer with batch
net.run(opt, feed_dict={X: batch_x, Y: batch_y})
# Show progress
if np.mod(i, 5) == 0:
# Prediction
pred = net.run(out, feed_dict={X: X_test})
line2.set_ydata(pred)
plt.title(‘Epoch ‘ + str(e) + ‘, Batch ‘ + str(i))
file_name = ‘img/epoch_’ + str(e) + ‘_batch_’ + str(i) + ‘.jpg’
plt.savefig(file_name)
plt.pause(0.01)
# Print final MSE after Training
mse_final = net.run(mse, feed_dict={X: X_test, Y: y_test})
print(mse_final)
在训练过程中,我们评估测试集上的网络预测数据 – 这些数据不是跟学习无关,而是额外保留的 – 每5批次进行一次可视化。此外,图像被导出到磁盘,然后组合成训练过程的视频动画(见下文)。该模型可以快速了解测试数据中时间序列的形状和位置,并能够在几轮epochs后产生准确的预测结果。太好了!
人们可以看到,网络很快适应时间序列的基本形状,并继续学习更精细的数据模式。这也对应于在模型训练期间降低学习速率的Adam学习方案,以便不超过优化最小值。经过10个epochs后,我们与测试数据非常接近!最终的测试MSE等于0.00078(这是非常低的,因为目标是缩放的)。测试集预测的平均绝对百分比误差等于5.31%,这相当不错。请注意,这仅适用于测试数据,实际情况下没有实际的样本量度。
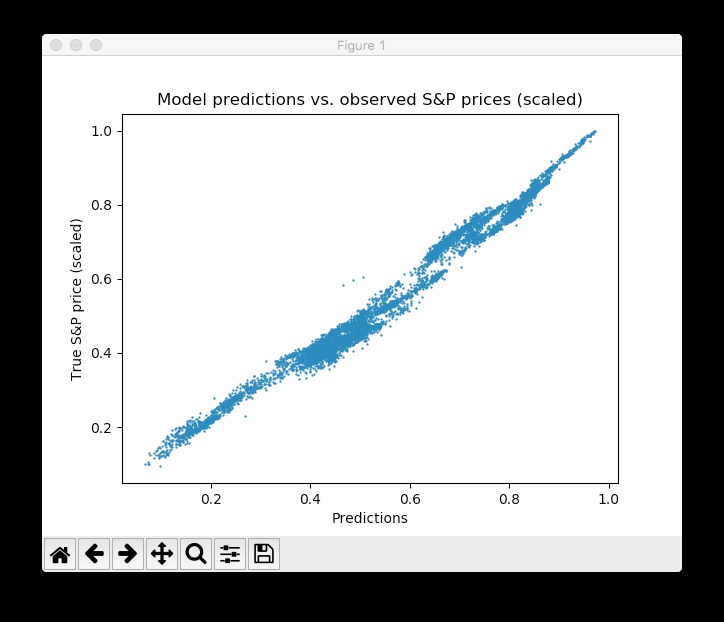
请注意,有很多方法可以进一步改善这一结果:设计图层和神经元,选择不同的初始化和激活方案,引入神经元丢失层,提前停止等等。此外,不同类型的深度学习模型(如递归神经网络)可能会在此任务中获得更好的性能。但是,这不是这篇介绍性文章的范围。
结论和展望
TensorFlow的发布是深度学习研究中的一个里程碑事件。其灵活性和性能使研究人员能够开发各种复杂的神经网络体系结构以及其他ML算法。然而,与较高级别的API相比,灵活性的代价是更长的time-to-model周期,例如Keras或MxNet。尽管如此,我确信TensorFlow将在神经网络和深入学习的研究和实际应用开发中走向de-facto标准。我们的许多客户已经在使用TensorFlow或开始开发使用TensorFlow模型的项目。我们的数据科学顾问在STATWORX大量使用TensorFlow进行深度学习和神经网络研究与开发。让我们看看Google为TensorFlow的未来计划了什么。至少在我看来,缺少的一件事是用TensorFlow后端设计和开发神经网络体系结构的整洁的图形用户界面。也许,这是Google正在处理的内容;)
更新:我已经将Python脚本和(压缩)数据集都添加到了一个Github存储库。请随意克隆和分支。
