我正使用TensorFlow來訓練一個神經網絡。我初始化GradientDescentOptimizer的方式如下:
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
mse = tf.reduce_mean(tf.square(out - out_))
train_step = tf.train.GradientDescentOptimizer(0.3).minimize(mse)
問題是我不知道如何為學習速率或衰減值設置更新規則。
如何在這裏使用自適應學習率呢?
最佳解決辦法
首先,tf.train.GradientDescentOptimizer旨在對所有步驟中的所有變量使用恒定的學習率。 TensorFlow還提供現成的自適應優化器,包括tf.train.AdagradOptimizer和tf.train.AdamOptimizer,這些可以作為隨時可用的替代品。
但是,如果要通過其他普通漸變下降控製學習速率,則可以利用以下事實:tf.train.GradientDescentOptimizer構造函數的learning_rate參數可以是Tensor對象。這允許您在每個步驟中為學習速率計算不同的值,例如:
learning_rate = tf.placeholder(tf.float32, shape=[])
# ...
train_step = tf.train.GradientDescentOptimizer(
learning_rate=learning_rate).minimize(mse)
sess = tf.Session()
# Feed different values for learning rate to each training step.
sess.run(train_step, feed_dict={learning_rate: 0.1})
sess.run(train_step, feed_dict={learning_rate: 0.1})
sess.run(train_step, feed_dict={learning_rate: 0.01})
sess.run(train_step, feed_dict={learning_rate: 0.01})
或者,您可以創建一個標量tf.Variable來保存學習率,並在每次要更改學習率時進行分配。
次佳解決辦法
Tensorflow提供了一種自動將指數衰減應用於學習速率張量的操作:tf.train.exponential_decay。有關正在使用的示例,請參閱this line in the MNIST convolutional model example。然後使用前文中的建議將此變量作為learning_rate參數提供給您的優化器。
要看的關鍵部分是:
# Optimizer: set up a variable that's incremented once per batch and
# controls the learning rate decay.
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
0.01, # Base learning rate.
batch * BATCH_SIZE, # Current index into the dataset.
train_size, # Decay step.
0.95, # Decay rate.
staircase=True)
# Use simple momentum for the optimization.
optimizer = tf.train.MomentumOptimizer(learning_rate,
0.9).minimize(loss,
global_step=batch)
注意最小化global_step=batch參數。這會告訴優化器在每次訓練時都會幫助您增加’batch’參數。
第三種解決辦法
梯度下降算法使您可以在during the initialization中提供的恒定的學習速率。可以通過前文所示的方式傳遞各種學習速率。
但是,也可以使用more advanced optimizers,它具有更快的收斂速度並適應這種情況。
根據我的理解,這裏是一個簡短的解釋:
- 動量(momentum)helps SGD沿相關方向導航,並減弱無關的振蕩。它隻是將上一步驟的一部分方向添加到當前步驟。這可以在正確的方向上實現放大速度,並減少錯誤方向的振蕩。該分數通常在(0,1)範圍內。使用自適應動量也是有意義的。在學習開始時,一個大的動量隻會阻礙你的進步,所以使用類似0.01的數值很有意義,一旦所有的高梯度消失,你可以使用更大的動量。動量也有一個問題:當我們非常接近目標時,我們在大多數情況下的動量非常高,而且它不知道它應該放慢速度。這可能導致它錯過或在最低點附近振蕩
- 內斯特洛夫加速梯度(nesterov accelerated gradient, NAG)通過開始減速提前克服了這個問題。在動量中,我們首先計算梯度,然後通過先前的任何動量放大該方向的跳躍。 NAG做的是同樣的事情,但是按照另一種順序:首先我們根據存儲的信息做出一個大的跳躍,然後我們計算梯度並進行一個小的修正。這個看似不相關的變化給了顯著的實際加速。
- AdaGrad或自適應梯度允許學習速率根據參數進行調整。它對不頻繁的參數執行更大的更新,對頻繁的參數執行更小的更新。正因為如此,它非常適合稀疏數據(NLP或圖像識別)。另一個優點是它基本上不需要調整學習速度。每個參數都有其自己的學習速率,並且由於算法的特性,學習速率是單調遞減的。這導致了最大的問題:在某個時間點,學習率很低,係統停止學習
- AdaDelta解決了AdaGrad中單調降低學習率的問題。在AdaGrad中,學習率大致被計算為除以平方根之和。在每個階段,您都會在總和中再加一個平方根,這會導致分母不斷下降。在AdaDelta中,不是將所有過去的平方根相加,而是使用允許總和減少的滑動窗口。 RMSprop與AdaDelta非常相似
- Adam或自適應動量是一種類似於AdaDelta的算法。但除了存儲每個參數的學習率外,它還分別存儲每個參數的動量變化A few visualizations:

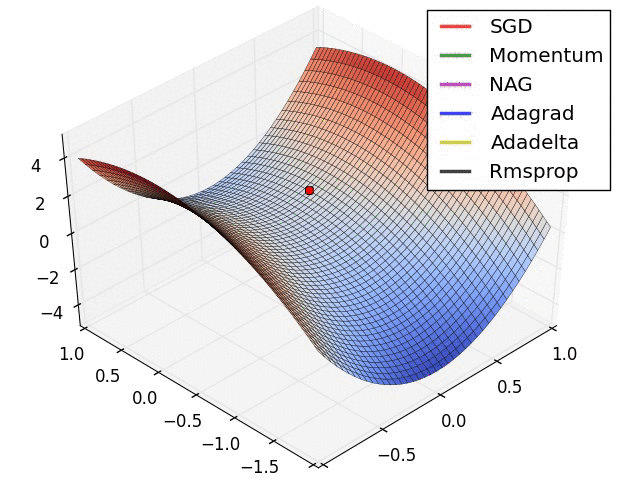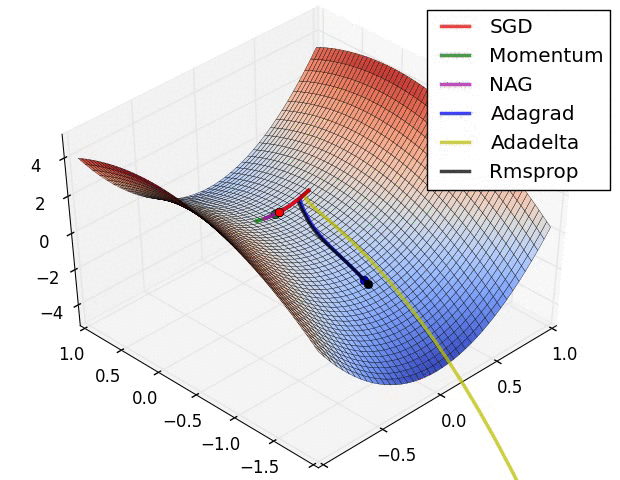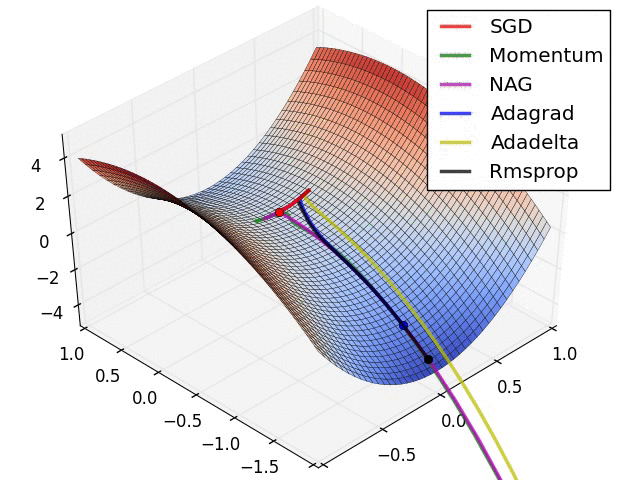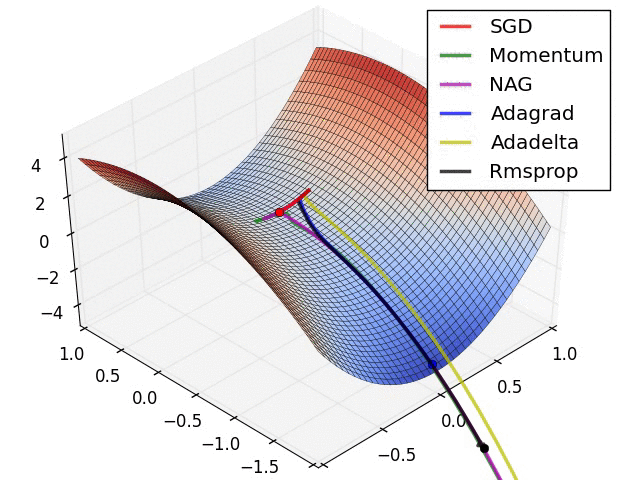
參考資料
