本文簡要介紹 python 語言中 scipy.special.it2i0k0 的用法。
用法:
scipy.special.it2i0k0(x, out=None) = <ufunc 'it2i0k0'>#與 0 階修正貝塞爾函數相關的積分。
計算積分
- x: array_like
評估積分的值。
- out: ndarrays 元組,可選
函數結果的可選輸出數組。
參數 ::
返回 ::
參考:
[1]S. 張和 J.M. Jin,“特殊函數的計算”,Wiley 1996
例子:
在某一點評估函數。
>>> from scipy.special import it2i0k0 >>> int_i, int_k = it2i0k0(1.) >>> int_i, int_k (0.12897944249456852, 0.2085182909001295)在幾個點上評估函數。
>>> import numpy as np >>> points = np.array([0.5, 1.5, 3.]) >>> int_i, int_k = it2i0k0(points) >>> int_i, int_k (array([0.03149527, 0.30187149, 1.50012461]), array([0.66575102, 0.0823715 , 0.00823631]))繪製從 0 到 5 的函數。
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> x = np.linspace(0., 5., 1000) >>> int_i, int_k = it2i0k0(x) >>> ax.plot(x, int_i, label=r"$\int_0^x \frac{I_0(t)-1}{t}\,dt$") >>> ax.plot(x, int_k, label=r"$\int_x^{\infty} \frac{K_0(t)}{t}\,dt$") >>> ax.legend() >>> ax.set_ylim(0, 10) >>> plt.show()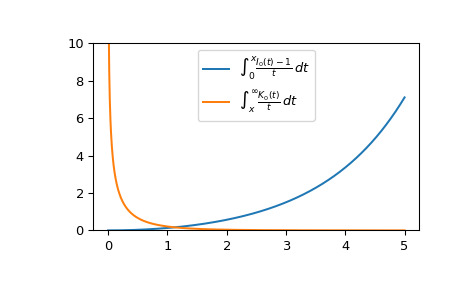
相關用法
- Python SciPy special.it2struve0用法及代碼示例
- Python SciPy special.it2j0y0用法及代碼示例
- Python SciPy special.iti0k0用法及代碼示例
- Python SciPy special.itmodstruve0用法及代碼示例
- Python SciPy special.itstruve0用法及代碼示例
- Python SciPy special.itj0y0用法及代碼示例
- Python SciPy special.itairy用法及代碼示例
- Python SciPy special.i1e用法及代碼示例
- Python SciPy special.inv_boxcox用法及代碼示例
- Python SciPy special.ivp用法及代碼示例
- Python SciPy special.ive用法及代碼示例
- Python SciPy special.i0e用法及代碼示例
- Python SciPy special.inv_boxcox1p用法及代碼示例
- Python SciPy special.iv用法及代碼示例
- Python SciPy special.i1用法及代碼示例
- Python SciPy special.i0用法及代碼示例
- Python SciPy special.exp1用法及代碼示例
- Python SciPy special.expn用法及代碼示例
- Python SciPy special.ncfdtri用法及代碼示例
- Python SciPy special.gamma用法及代碼示例
- Python SciPy special.y1用法及代碼示例
- Python SciPy special.y0用法及代碼示例
- Python SciPy special.ellip_harm_2用法及代碼示例
- Python SciPy special.smirnovi用法及代碼示例
- Python SciPy special.ker用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.special.it2i0k0。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
