本文簡要介紹 python 語言中 scipy.special.chebyt 的用法。
用法:
scipy.special.chebyt(n, monic=False)#第一類切比雪夫多項式。
定義為解決方案
是一次多項式 。
- n: int
多項式的次數。
- monic: 布爾型,可選
如果為 True,則將前導係數縮放為 1。默認為 False。
- T: orthopoly1d
第一類切比雪夫多項式。
參數 ::
返回 ::
注意:
多項式 與 正交,權重函數為 。
參考:
[AS]Milton Abramowitz 和 Irene A. Stegun 合編。帶有公式、圖表和數學表格的數學函數手冊。紐約:多佛,1972 年。
例子:
第一類 的切比雪夫多項式可以作為特定 矩陣的行列式獲得。例如,我們可以檢查從以下 矩陣的行列式獲得的點如何準確地放置在 上:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.linalg import det >>> from scipy.special import chebyt >>> x = np.arange(-1.0, 1.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-2.0, 2.0) >>> ax.set_title(r'Chebyshev polynomial $T_3$') >>> ax.plot(x, chebyt(3)(x), label=rf'$T_3$') >>> for p in np.arange(-1.0, 1.0, 0.1): ... ax.plot(p, ... det(np.array([[p, 1, 0], [1, 2*p, 1], [0, 1, 2*p]])), ... 'rx') >>> plt.legend(loc='best') >>> plt.show()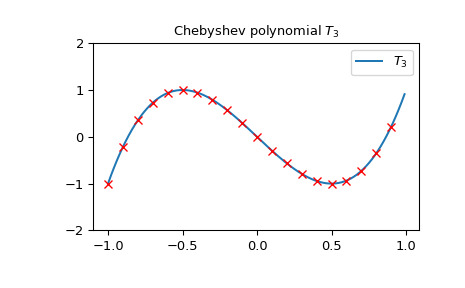
它們還通過以下關係與 Jacobi 多項式 相關:
讓我們為 驗證它:
>>> from scipy.special import binom >>> from scipy.special import jacobi >>> x = np.arange(-1.0, 1.0, 0.01) >>> np.allclose(jacobi(3, -0.5, -0.5)(x), ... 1/64 * binom(6, 3) * chebyt(3)(x)) True我們可以為 的某些值繪製切比雪夫多項式 :
>>> x = np.arange(-1.5, 1.5, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-4.0, 4.0) >>> ax.set_title(r'Chebyshev polynomials $T_n$') >>> for n in np.arange(2,5): ... ax.plot(x, chebyt(n)(x), label=rf'$T_n={n}$') >>> plt.legend(loc='best') >>> plt.show()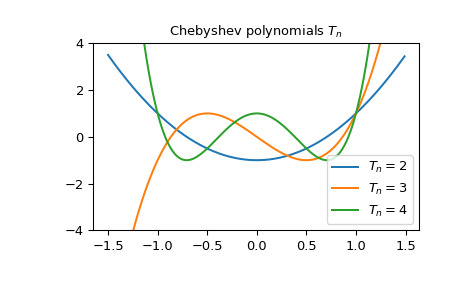
相關用法
- Python SciPy special.chebyu用法及代碼示例
- Python SciPy special.chdtr用法及代碼示例
- Python SciPy special.chdtriv用法及代碼示例
- Python SciPy special.chdtrc用法及代碼示例
- Python SciPy special.chdtri用法及代碼示例
- Python SciPy special.comb用法及代碼示例
- Python SciPy special.cbrt用法及代碼示例
- Python SciPy special.cosdg用法及代碼示例
- Python SciPy special.cosm1用法及代碼示例
- Python SciPy special.cotdg用法及代碼示例
- Python SciPy special.exp1用法及代碼示例
- Python SciPy special.expn用法及代碼示例
- Python SciPy special.ncfdtri用法及代碼示例
- Python SciPy special.gamma用法及代碼示例
- Python SciPy special.y1用法及代碼示例
- Python SciPy special.y0用法及代碼示例
- Python SciPy special.ellip_harm_2用法及代碼示例
- Python SciPy special.i1e用法及代碼示例
- Python SciPy special.smirnovi用法及代碼示例
- Python SciPy special.ker用法及代碼示例
- Python SciPy special.ynp_zeros用法及代碼示例
- Python SciPy special.k0e用法及代碼示例
- Python SciPy special.j1用法及代碼示例
- Python SciPy special.logsumexp用法及代碼示例
- Python SciPy special.expit用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.special.chebyt。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
