本文簡要介紹 python 語言中 scipy.linalg.lstsq 的用法。
用法:
scipy.linalg.lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)#計算方程 Ax = b 的最小二乘解。
計算一個向量 x 以使 2-範數
|b - A x|最小化。- a: (M, N) 數組
左側數組
- b: (M,) 或 (M, K) 數組
右側陣列
- cond: 浮點數,可選
‘small’ 奇異值的截止值;用於確定a的有效等級。小於
cond * largest_singular_value的奇異值被視為零。- overwrite_a: 布爾型,可選
丟棄 a 中的數據(可能會提高性能)。默認為假。
- overwrite_b: 布爾型,可選
丟棄 b 中的數據(可能會提高性能)。默認為假。
- check_finite: 布爾型,可選
是否檢查輸入矩陣是否僅包含有限數。禁用可能會提高性能,但如果輸入確實包含無窮大或 NaN,則可能會導致問題(崩潰、非終止)。
- lapack_driver: str,可選
哪個LAPACK驅動程序是用來解決最小二乘問題的。選項有
'gelsd'、'gelsy'、'gelss'。默認('gelsd')是一個不錯的選擇。然而,'gelsy'在許多問題上可以稍微快一些。'gelss'曆史上曾被使用過。它通常很慢,但使用的內存較少。
- x: (N,) 或 (N, K) ndarray
最小二乘解。
- residues: (K,) ndarray 或浮點數
b - a x中每一列的 2 範數的平方,如果M > N和ndim(A) == n(如果b是一維則返回一個標量)。否則返回 (0,) 形數組。- rank: int
a. 有效等級
- s: (min(M, N),) ndarray 或無
的奇異值a.條件數
a是s[0] / s[-1].
- LinAlgError
如果計算不收斂。
- ValueError
當參數不兼容時。
參數 ::
返回 ::
拋出 ::
注意:
什麽時候
'gelsy'用作驅動程序,殘留物設置為 (0,) 形數組和s總是None.例子:
>>> import numpy as np >>> from scipy.linalg import lstsq >>> import matplotlib.pyplot as plt假設我們有以下數據:
>>> x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5]) >>> y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])我們希望將
y = a + b*x**2形式的二次多項式擬合到該數據。我們首先形成“design matrix” M,其中有一列常量為 1,一列包含x**2:>>> M = x[:, np.newaxis]**[0, 2] >>> M array([[ 1. , 1. ], [ 1. , 6.25], [ 1. , 12.25], [ 1. , 16. ], [ 1. , 25. ], [ 1. , 49. ], [ 1. , 72.25]])我們想要找到
M.dot(p) = y的最小二乘解,其中p是長度為 2 的向量,其中包含參數a和b。>>> p, res, rnk, s = lstsq(M, y) >>> p array([ 0.20925829, 0.12013861])繪製數據和擬合曲線。
>>> plt.plot(x, y, 'o', label='data') >>> xx = np.linspace(0, 9, 101) >>> yy = p[0] + p[1]*xx**2 >>> plt.plot(xx, yy, label='least squares fit, $y = a + bx^2$') >>> plt.xlabel('x') >>> plt.ylabel('y') >>> plt.legend(framealpha=1, shadow=True) >>> plt.grid(alpha=0.25) >>> plt.show()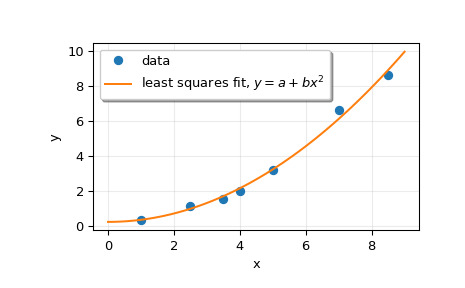
相關用法
- Python SciPy linalg.lsqr用法及代碼示例
- Python SciPy linalg.lsmr用法及代碼示例
- Python SciPy linalg.lu_factor用法及代碼示例
- Python SciPy linalg.lu_solve用法及代碼示例
- Python SciPy linalg.lu用法及代碼示例
- Python SciPy linalg.logm用法及代碼示例
- Python SciPy linalg.ldl用法及代碼示例
- Python SciPy linalg.leslie用法及代碼示例
- Python SciPy linalg.lobpcg用法及代碼示例
- Python SciPy linalg.lgmres用法及代碼示例
- Python SciPy linalg.eigvalsh_tridiagonal用法及代碼示例
- Python SciPy linalg.cdf2rdf用法及代碼示例
- Python SciPy linalg.LaplacianNd用法及代碼示例
- Python SciPy linalg.solve_circulant用法及代碼示例
- Python SciPy linalg.polar用法及代碼示例
- Python SciPy linalg.clarkson_woodruff_transform用法及代碼示例
- Python SciPy linalg.rsf2csf用法及代碼示例
- Python SciPy linalg.hessenberg用法及代碼示例
- Python SciPy linalg.tril用法及代碼示例
- Python SciPy linalg.triu用法及代碼示例
- Python SciPy linalg.svd用法及代碼示例
- Python SciPy linalg.ishermitian用法及代碼示例
- Python SciPy linalg.invhilbert用法及代碼示例
- Python SciPy linalg.factorized用法及代碼示例
- Python SciPy linalg.SuperLU用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.linalg.lstsq。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
