Python PyTorch log2()用法及代码示例

PyTorch log2() 方法计算输入张量元素以 2 为底的对数。它按元素计算对数值。它将张量作为输入并返回具有计算对数值的新张量。输入张量的元素必须介于零和正无穷大之间，作为函数 log 的域₂(x) 为 (0, ∞)。我们将对此方法使用以下语法 -

用法： torch.log2(input, out=None)

让我们借助一些 Python 3 程序示例来了解 torch.log2() 方法。

示例 1：

在此示例中，我们定义一个一维张量，并计算其元素以 2 为底的值的对数。

# Python3 program to demonstrate torch.log2() method
# importing torch
import torch
# defining a torch tensor
t = torch.tensor([2., 4., 7., 3.])
print('Tensor:', t)
# computing the logarithm base 2 of t
result = torch.log2(t)
print('Logarithm of Tensor:', result)

输出：

Tensor: tensor([2., 4., 7., 3.])

Logarithm of Tensor: tensor([1.0000, 2.0000, 2.8074, 1.5850])

说明： 对数是按元素计算的。

示例 2：

在下面的示例中，我们计算 2D 张量以 2 为底的对数。

# Python3 program to demonstrate torch.log2() method
# for 2D tensors
# importing torch
import torch
# defining a 2D torch tensor with numbers sampled
# from the discrete uniform distribution
t = torch.empty((3, 4), dtype=torch.float32).random_(1, 50)
print('Tensor:\n', t)
# computing the logarithm base 2 of t
result = torch.log2(t)
print('Logarithm of Tensor:\n', result)

输出：

Tensor:
 tensor([[19., 32.,  2., 29.],
        [30., 10., 16., 18.],
        [49., 10.,  7., 25.]])
Logarithm of Tensor:
 tensor([[4.2479, 5.0000, 1.0000, 4.8580],
        [4.9069, 3.3219, 4.0000, 4.1699],
        [5.6147, 3.3219, 2.8074, 4.6439]])

说明：请注意，上述代码中的输入张量是用从离散均匀分布中采样的数字生成的，因此当您执行代码时可能会生成不同的数字。

示例 3：

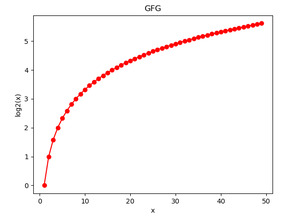
在下面的示例中，我们计算输入张量元素以 2 为底的对数，并借助 Matplotlib 图可视化结果。

# Python3 program to demonstrate torch.log2() method
%matplotlib qt 
# importing required libraries
import torch
import numpy as np
# import matplotlib.pyplot as plt
# defining a torch tensor
x = np.arange(1,50, 1)
t = torch.tensor(x)
print('Tensor:', t)
# computing the logarithm base 2 of t
result = torch.log2(t)
print('Logarithm of Tensor:', result)
# tensor to numpy array
y = result.numpy()
# plot the result using matplotlib
plt.plot(x, y, color = 'red', marker = "o") 
plt.xlabel("x") 
plt.ylabel("log2(x)") 
plt.show()

输出：

Tensor: tensor([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18,

        19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36,

        37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49], dtype=torch.int32)

Logarithm of Tensor: tensor([0.0000, 1.0000, 1.5850, 2.0000, 2.3219, 2.5850, 2.8074, 3.0000, 3.1699,

        3.3219, 3.4594, 3.5850, 3.7004, 3.8074, 3.9069, 4.0000, 4.0875, 4.1699,

        4.2479, 4.3219, 4.3923, 4.4594, 4.5236, 4.5850, 4.6439, 4.7004, 4.7549,

        4.8074, 4.8580, 4.9069, 4.9542, 5.0000, 5.0444, 5.0875, 5.1293, 5.1699,

        5.2095, 5.2479, 5.2854, 5.3219, 5.3576, 5.3923, 5.4263, 5.4594, 5.4919,

        5.5236, 5.5546, 5.5850, 5.6147])

示例4：

在此示例中，我们尝试计算负值、零值和无穷大值的以 2 为底的对数。看看输出如何。

# Python3 program to demonstrate torch.log2() method
# importing libraries
import torch
import numpy as np
# defining a torch tensor
t = torch.tensor([-3., -5., 0, 0.5, 7., 3., np.inf])
print('Original Tensor:\n', t)
# computing the logarithm base 2 of t
result = torch.log2(t)
print('Logarithm of Tensor:\n', result)

输出：

Original Tensor:

 tensor([-3.0000, -5.0000,  0.0000,  0.5000,  7.0000,  3.0000,     inf])

Logarithm of Tensor:

 tensor([    nan,     nan,    -inf, -1.0000,  2.8074,  1.5850,     inf])

解释：看到负数的对数是nan(Not a Number)。 0的对数是-inf。无穷大的对数就是无穷大(inf)。