本文简要介绍 python 语言中 numpy.percentile 的用法。
用法:
numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, method='linear', keepdims=False, *, interpolation=None)沿指定轴计算数据的q-th 百分位数。
返回数组元素的 q-th 百分位数。
- a: array_like
可以转换为数组的输入数组或对象。
- q: 类似浮点数的数组
要计算的百分位数或百分位数序列,必须介于 0 和 100 之间。
- axis: {int,int 元组,无},可选
计算百分位数的一个或多个轴。默认值是沿阵列的展平版本计算百分位数。
- out: ndarray,可选
用于放置结果的替代输出数组。它必须具有与预期输出相同的形状和缓冲区长度,但如有必要,将强制转换(输出的)类型。
- overwrite_input: 布尔型,可选
如果为 True,则允许通过中间计算修改输入数组 a,以节省内存。在这种情况下,该函数完成后输入 a 的内容是未定义的。
- method: str,可选
此参数指定用于估计百分位数的方法。有许多不同的方法,其中一些是 NumPy 独有的。请参阅注释以获取解释。 H&F; 论文 [1] 中总结的按 R 类型排序的选项为:
‘inverted_cdf’
‘averaged_inverted_cdf’
‘closest_observation’
‘interpolated_inverted_cdf’
‘hazen’
‘weibull’
‘linear’(默认)
‘median_unbiased’
‘normal_unbiased’
前三种方法是不连续的。 NumPy 进一步定义了默认 ‘linear’ (7.) 选项的以下不连续变体:
‘lower’
‘higher’,
‘midpoint’
‘nearest’
- keepdims: 布尔型,可选
如果将其设置为 True,则缩小的轴将作为尺寸为 1 的尺寸留在结果中。使用此选项,结果将针对原始数组 a 正确广播。
- interpolation: str,可选
方法关键字参数的已弃用名称。
- percentile: 标量或 ndarray
如果q是一个百分位数并且轴=无, 那么结果是一个标量。如果给出多个百分位数,则结果的第一个轴对应于百分位数。其他轴是减少后剩余的轴a.如果输入包含整数或浮点数小于
float64,输出数据类型为float64.否则,输出数据类型与输入数据类型相同。如果out指定,则返回该数组。
参数:
返回:
注意:
给定一个向量
V长度N, q-th 的百分位数V是值q/100的排序副本中从最小值到最大值的方式V.两个最近邻居的值和距离以及方法如果归一化排名与位置不匹配,参数将确定百分位数q确切地。此函数与中位数相同 ifq=50,与最小值相同,如果q=0并且与最大值相同 ifq=100.这个可选方法参数指定当所需分位数位于两个数据点之间时使用的方法
i < j.如果g是被包围的索引的小数部分i和 alpha 和 beta 是修正 i 和 j 的修正常数。下面,‘q’ 是分位数,‘n’ 是样本大小,alpha 和 beta 是常数。下面的公式给出了分位数在排序样本中的插值“i + g”。 ‘i’ 是底数,‘g’ 是结果的小数部分。
然后不同的方法如下工作
H&F; 的方法 1 [1]。此方法给出不连续的结果: * if g > 0 ;如果 g = 0,则取 j * ;然后带我
H&F; 的方法 2 [1]。此方法给出不连续的结果: * if g > 0 ;如果 g = 0,则取 j * ;然后在边界之间求平均值
H&F; 的方法 3 [1]。此方法给出不连续的结果: * if g > 0 ;如果 g = 0 并且索引为奇数,则取 j * ;如果 g = 0 并且索引为偶数,则取 j * ;然后带我
H&F; 的方法 4 [1]。此方法使用以下方法给出连续结果: * alpha = 0 * beta = 1
H&F; 的方法 5 [1]。此方法使用以下方法给出连续结果: * alpha = 1/2 * beta = 1/2
H&F; 的方法 6 [1]。此方法使用以下方法给出连续结果: * alpha = 0 * beta = 0
H&F; 的方法 7 [1]。此方法使用以下方法给出连续结果: * alpha = 1 * beta = 1
H&F; 的方法 8 [1]。如果样本分布函数未知(请参阅引用),此方法可能是最好的方法。此方法使用以下方法给出连续结果: * alpha = 1/3 * beta = 1/3
H&F; 的方法 9 [1]。如果已知样本分布函数是正态的,则此方法可能是最好的方法。此方法使用以下方法给出连续结果: * alpha = 3/8 * beta = 3/8
NumPy 方法保留是为了向后兼容。以
i为插值点。NumPy 方法保留是为了向后兼容。以
j为插值点。NumPy 方法保留是为了向后兼容。采用
i或j,以最近者为准。NumPy 方法保留是为了向后兼容。使用
(i + j) / 2。
inverted_cdf::
averaged_inverted_cdf::
closest_observation::
interpolated_inverted_cdf::
hazen::
weibull::
linear::
median_unbiased::
normal_unbiased::
lower::
higher::
nearest::
midpoint::
参考:
R. J. Hyndman 和 Y. Fan,“统计包中的样本分位数”,美国统计学家,50(4),第 361-365 页,1996
1 [1,2,3,4,5,6,7,8,9 和 10]:
例子:
>>> a = np.array([[10, 7, 4], [3, 2, 1]]) >>> a array([[10, 7, 4], [ 3, 2, 1]]) >>> np.percentile(a, 50) 3.5 >>> np.percentile(a, 50, axis=0) array([6.5, 4.5, 2.5]) >>> np.percentile(a, 50, axis=1) array([7., 2.]) >>> np.percentile(a, 50, axis=1, keepdims=True) array([[7.], [2.]])>>> m = np.percentile(a, 50, axis=0) >>> out = np.zeros_like(m) >>> np.percentile(a, 50, axis=0, out=out) array([6.5, 4.5, 2.5]) >>> m array([6.5, 4.5, 2.5])>>> b = a.copy() >>> np.percentile(b, 50, axis=1, overwrite_input=True) array([7., 2.]) >>> assert not np.all(a == b)不同的方法可以用图形表示:
import matplotlib.pyplot as plt a = np.arange(4) p = np.linspace(0, 100, 6001) ax = plt.gca() lines = [ ('linear', '-', 'C0'), ('inverted_cdf', ':', 'C1'), # Almost the same as `inverted_cdf`: ('averaged_inverted_cdf', '-.', 'C1'), ('closest_observation', ':', 'C2'), ('interpolated_inverted_cdf', '--', 'C1'), ('hazen', '--', 'C3'), ('weibull', '-.', 'C4'), ('median_unbiased', '--', 'C5'), ('normal_unbiased', '-.', 'C6'), ] for method, style, color in lines: ax.plot( p, np.percentile(a, p, method=method), label=method, linestyle=style, color=color) ax.set( title='Percentiles for different methods and data: ' + str(a), xlabel='Percentile', ylabel='Estimated percentile value', yticks=a) ax.legend() plt.show()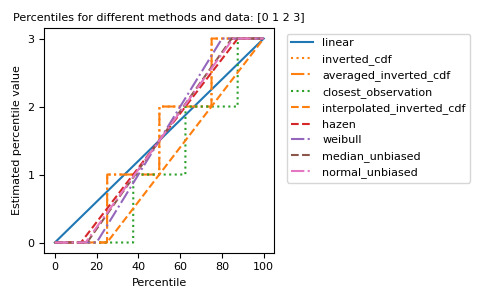
相关用法
- Python numpy polyder用法及代码示例
- Python numpy polynomial.polyfit用法及代码示例
- Python numpy put_along_axis用法及代码示例
- Python numpy polyfit用法及代码示例
- Python numpy piecewise用法及代码示例
- Python numpy polynomial.polyline用法及代码示例
- Python numpy polynomial.polyadd用法及代码示例
- Python numpy polynomial.polyder用法及代码示例
- Python numpy pmt用法及代码示例
- Python numpy promote_types用法及代码示例
- Python numpy polyutils.as_series用法及代码示例
- Python numpy polynomial.polydomain用法及代码示例
- Python numpy poly用法及代码示例
- Python numpy polynomial.polyint用法及代码示例
- Python numpy polysub用法及代码示例
- Python numpy prod用法及代码示例
- Python numpy polyutils.getdomain用法及代码示例
- Python numpy power用法及代码示例
- Python numpy polyutils.mapdomain用法及代码示例
- Python numpy putmask用法及代码示例
- Python numpy polyutils.mapparms用法及代码示例
- Python numpy polynomial.polydiv用法及代码示例
- Python numpy polynomial.polyvalfromroots用法及代码示例
- Python numpy polydiv用法及代码示例
- Python numpy polynomial.polyval用法及代码示例
注:本文由纯净天空筛选整理自numpy.org大神的英文原创作品 numpy.percentile。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
