本文簡要介紹 python 語言中 numpy.percentile 的用法。
用法:
numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, method='linear', keepdims=False, *, interpolation=None)沿指定軸計算數據的q-th 百分位數。
返回數組元素的 q-th 百分位數。
- a: array_like
可以轉換為數組的輸入數組或對象。
- q: 類似浮點數的數組
要計算的百分位數或百分位數序列,必須介於 0 和 100 之間。
- axis: {int,int 元組,無},可選
計算百分位數的一個或多個軸。默認值是沿陣列的展平版本計算百分位數。
- out: ndarray,可選
用於放置結果的替代輸出數組。它必須具有與預期輸出相同的形狀和緩衝區長度,但如有必要,將強製轉換(輸出的)類型。
- overwrite_input: 布爾型,可選
如果為 True,則允許通過中間計算修改輸入數組 a,以節省內存。在這種情況下,該函數完成後輸入 a 的內容是未定義的。
- method: str,可選
此參數指定用於估計百分位數的方法。有許多不同的方法,其中一些是 NumPy 獨有的。請參閱注釋以獲取解釋。 H&F; 論文 [1] 中總結的按 R 類型排序的選項為:
‘inverted_cdf’
‘averaged_inverted_cdf’
‘closest_observation’
‘interpolated_inverted_cdf’
‘hazen’
‘weibull’
‘linear’(默認)
‘median_unbiased’
‘normal_unbiased’
前三種方法是不連續的。 NumPy 進一步定義了默認 ‘linear’ (7.) 選項的以下不連續變體:
‘lower’
‘higher’,
‘midpoint’
‘nearest’
- keepdims: 布爾型,可選
如果將其設置為 True,則縮小的軸將作為尺寸為 1 的尺寸留在結果中。使用此選項,結果將針對原始數組 a 正確廣播。
- interpolation: str,可選
方法關鍵字參數的已棄用名稱。
- percentile: 標量或 ndarray
如果q是一個百分位數並且軸=無, 那麽結果是一個標量。如果給出多個百分位數,則結果的第一個軸對應於百分位數。其他軸是減少後剩餘的軸a.如果輸入包含整數或浮點數小於
float64,輸出數據類型為float64.否則,輸出數據類型與輸入數據類型相同。如果out指定,則返回該數組。
參數:
返回:
注意:
給定一個向量
V長度N, q-th 的百分位數V是值q/100的排序副本中從最小值到最大值的方式V.兩個最近鄰居的值和距離以及方法如果歸一化排名與位置不匹配,參數將確定百分位數q確切地。此函數與中位數相同 ifq=50,與最小值相同,如果q=0並且與最大值相同 ifq=100.這個可選方法參數指定當所需分位數位於兩個數據點之間時使用的方法
i < j.如果g是被包圍的索引的小數部分i和 alpha 和 beta 是修正 i 和 j 的修正常數。下麵,‘q’ 是分位數,‘n’ 是樣本大小,alpha 和 beta 是常數。下麵的公式給出了分位數在排序樣本中的插值“i + g”。 ‘i’ 是底數,‘g’ 是結果的小數部分。
然後不同的方法如下工作
H&F; 的方法 1 [1]。此方法給出不連續的結果: * if g > 0 ;如果 g = 0,則取 j * ;然後帶我
H&F; 的方法 2 [1]。此方法給出不連續的結果: * if g > 0 ;如果 g = 0,則取 j * ;然後在邊界之間求平均值
H&F; 的方法 3 [1]。此方法給出不連續的結果: * if g > 0 ;如果 g = 0 並且索引為奇數,則取 j * ;如果 g = 0 並且索引為偶數,則取 j * ;然後帶我
H&F; 的方法 4 [1]。此方法使用以下方法給出連續結果: * alpha = 0 * beta = 1
H&F; 的方法 5 [1]。此方法使用以下方法給出連續結果: * alpha = 1/2 * beta = 1/2
H&F; 的方法 6 [1]。此方法使用以下方法給出連續結果: * alpha = 0 * beta = 0
H&F; 的方法 7 [1]。此方法使用以下方法給出連續結果: * alpha = 1 * beta = 1
H&F; 的方法 8 [1]。如果樣本分布函數未知(請參閱引用),此方法可能是最好的方法。此方法使用以下方法給出連續結果: * alpha = 1/3 * beta = 1/3
H&F; 的方法 9 [1]。如果已知樣本分布函數是正態的,則此方法可能是最好的方法。此方法使用以下方法給出連續結果: * alpha = 3/8 * beta = 3/8
NumPy 方法保留是為了向後兼容。以
i為插值點。NumPy 方法保留是為了向後兼容。以
j為插值點。NumPy 方法保留是為了向後兼容。采用
i或j,以最近者為準。NumPy 方法保留是為了向後兼容。使用
(i + j) / 2。
inverted_cdf::
averaged_inverted_cdf::
closest_observation::
interpolated_inverted_cdf::
hazen::
weibull::
linear::
median_unbiased::
normal_unbiased::
lower::
higher::
nearest::
midpoint::
參考:
R. J. Hyndman 和 Y. Fan,“統計包中的樣本分位數”,美國統計學家,50(4),第 361-365 頁,1996
1 [1,2,3,4,5,6,7,8,9 和 10]:
例子:
>>> a = np.array([[10, 7, 4], [3, 2, 1]]) >>> a array([[10, 7, 4], [ 3, 2, 1]]) >>> np.percentile(a, 50) 3.5 >>> np.percentile(a, 50, axis=0) array([6.5, 4.5, 2.5]) >>> np.percentile(a, 50, axis=1) array([7., 2.]) >>> np.percentile(a, 50, axis=1, keepdims=True) array([[7.], [2.]])>>> m = np.percentile(a, 50, axis=0) >>> out = np.zeros_like(m) >>> np.percentile(a, 50, axis=0, out=out) array([6.5, 4.5, 2.5]) >>> m array([6.5, 4.5, 2.5])>>> b = a.copy() >>> np.percentile(b, 50, axis=1, overwrite_input=True) array([7., 2.]) >>> assert not np.all(a == b)不同的方法可以用圖形表示:
import matplotlib.pyplot as plt a = np.arange(4) p = np.linspace(0, 100, 6001) ax = plt.gca() lines = [ ('linear', '-', 'C0'), ('inverted_cdf', ':', 'C1'), # Almost the same as `inverted_cdf`: ('averaged_inverted_cdf', '-.', 'C1'), ('closest_observation', ':', 'C2'), ('interpolated_inverted_cdf', '--', 'C1'), ('hazen', '--', 'C3'), ('weibull', '-.', 'C4'), ('median_unbiased', '--', 'C5'), ('normal_unbiased', '-.', 'C6'), ] for method, style, color in lines: ax.plot( p, np.percentile(a, p, method=method), label=method, linestyle=style, color=color) ax.set( title='Percentiles for different methods and data: ' + str(a), xlabel='Percentile', ylabel='Estimated percentile value', yticks=a) ax.legend() plt.show()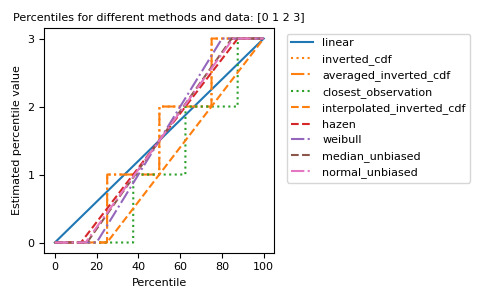
相關用法
- Python numpy polyder用法及代碼示例
- Python numpy polynomial.polyfit用法及代碼示例
- Python numpy put_along_axis用法及代碼示例
- Python numpy polyfit用法及代碼示例
- Python numpy piecewise用法及代碼示例
- Python numpy polynomial.polyline用法及代碼示例
- Python numpy polynomial.polyadd用法及代碼示例
- Python numpy polynomial.polyder用法及代碼示例
- Python numpy pmt用法及代碼示例
- Python numpy promote_types用法及代碼示例
- Python numpy polyutils.as_series用法及代碼示例
- Python numpy polynomial.polydomain用法及代碼示例
- Python numpy poly用法及代碼示例
- Python numpy polynomial.polyint用法及代碼示例
- Python numpy polysub用法及代碼示例
- Python numpy prod用法及代碼示例
- Python numpy polyutils.getdomain用法及代碼示例
- Python numpy power用法及代碼示例
- Python numpy polyutils.mapdomain用法及代碼示例
- Python numpy putmask用法及代碼示例
- Python numpy polyutils.mapparms用法及代碼示例
- Python numpy polynomial.polydiv用法及代碼示例
- Python numpy polynomial.polyvalfromroots用法及代碼示例
- Python numpy polydiv用法及代碼示例
- Python numpy polynomial.polyval用法及代碼示例
注:本文由純淨天空篩選整理自numpy.org大神的英文原創作品 numpy.percentile。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
