本文簡要介紹 python 語言中 scipy.special.spherical_in 的用法。
用法:
scipy.special.spherical_in(n, z, derivative=False)#第一類修正球貝塞爾函數或其導數。
定義為[1],
其中是第一類修正貝塞爾函數。
- n: 整數,數組
Bessel 函數的階數 (n >= 0)。
- z: 複數或浮點數,數組
貝塞爾函數的參數。
- derivative: 布爾型,可選
如果為 True,則返回導數(而不是函數本身)的值。
- in: ndarray
參數 ::
返回 ::
注意:
該函數是使用其與第一類修正圓柱貝塞爾函數的定義關係來計算的。
使用關係 [2] 計算導數,
參考:
[AS]Milton Abramowitz 和 Irene A. Stegun 合編。帶有公式、圖表和數學表格的數學函數手冊。紐約:多佛,1972 年。
例子:
第一類 的修正球麵貝塞爾函數接受實數和複數第二個參數。他們可以返回一個複雜的類型:
>>> from scipy.special import spherical_in >>> spherical_in(0, 3+5j) (-1.1689867793369182-1.2697305267234222j) >>> type(spherical_in(0, 3+5j)) <class 'numpy.complex128'>我們可以在區間 中驗證 的注釋導數的關係:
>>> import numpy as np >>> x = np.arange(1.0, 2.0, 0.01) >>> np.allclose(spherical_in(3, x, True), ... spherical_in(2, x) - 4/x * spherical_in(3, x)) True前幾個 帶有真實參數:
>>> import matplotlib.pyplot as plt >>> x = np.arange(0.0, 6.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-0.5, 5.0) >>> ax.set_title(r'Modified spherical Bessel functions $i_n$') >>> for n in np.arange(0, 4): ... ax.plot(x, spherical_in(n, x), label=rf'$i_{n}$') >>> plt.legend(loc='best') >>> plt.show()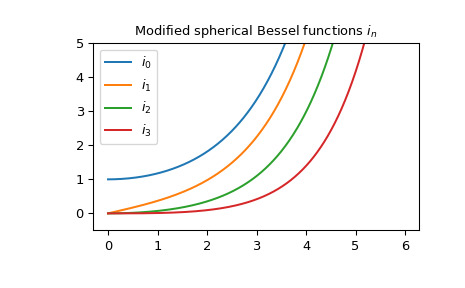
相關用法
- Python SciPy special.spherical_kn用法及代碼示例
- Python SciPy special.spherical_yn用法及代碼示例
- Python SciPy special.spherical_jn用法及代碼示例
- Python SciPy special.spence用法及代碼示例
- Python SciPy special.smirnovi用法及代碼示例
- Python SciPy special.seterr用法及代碼示例
- Python SciPy special.shichi用法及代碼示例
- Python SciPy special.smirnov用法及代碼示例
- Python SciPy special.stdtr用法及代碼示例
- Python SciPy special.softmax用法及代碼示例
- Python SciPy special.sinc用法及代碼示例
- Python SciPy special.stdtridf用法及代碼示例
- Python SciPy special.sindg用法及代碼示例
- Python SciPy special.struve用法及代碼示例
- Python SciPy special.sici用法及代碼示例
- Python SciPy special.stirling2用法及代碼示例
- Python SciPy special.stdtrit用法及代碼示例
- Python SciPy special.exp1用法及代碼示例
- Python SciPy special.expn用法及代碼示例
- Python SciPy special.ncfdtri用法及代碼示例
- Python SciPy special.gamma用法及代碼示例
- Python SciPy special.y1用法及代碼示例
- Python SciPy special.y0用法及代碼示例
- Python SciPy special.ellip_harm_2用法及代碼示例
- Python SciPy special.i1e用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.special.spherical_in。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
