本文簡要介紹 python 語言中scipy.interpolate.RectSphereBivariateSpline.__call__的用法。
用法:
RectSphereBivariateSpline.__call__(theta, phi, dtheta=0, dphi=0, grid=True)#評估給定位置處的樣條曲線或其導數。
- theta, phi: array_like
輸入坐標。
如果網格為 False,在點處評估樣條線
(theta[i], phi[i]), i=0, ..., len(x)-1。遵循標準 Numpy 廣播。如果網格為 True:在由坐標數組 theta、phi 定義的網格點處計算樣條線。數組必須按升序排序。軸的順序與
np.meshgrid(..., indexing="ij")並且與默認排序不一致np.meshgrid(..., indexing="xy").- dtheta: 整數,可選
theta-derivative的訂單
- dphi: int
phi-derivative的訂單
- grid: bool
是否在輸入數組跨越的網格上或在輸入數組指定的點上評估結果。
參數 ::
例子:
假設我們要使用樣條線在球體上插值二元函數。該函數的值在經度和緯度網格上已知。
>>> import numpy as np >>> from scipy.interpolate import RectSphereBivariateSpline >>> def f(theta, phi): ... return np.sin(theta) * np.cos(phi)我們評估網格上的函數。請注意,網格網格的默認索引 =”xy” 會導致插值後出現意外(轉置)結果。
>>> thetaarr = np.linspace(0, np.pi, 22)[1:-1] >>> phiarr = np.linspace(0, 2 * np.pi, 21)[:-1] >>> thetagrid, phigrid = np.meshgrid(thetaarr, phiarr, indexing="ij") >>> zdata = f(thetagrid, phigrid)接下來我們設置插值器並使用它在更精細的網格上評估函數。
>>> rsbs = RectSphereBivariateSpline(thetaarr, phiarr, zdata) >>> thetaarr_fine = np.linspace(0, np.pi, 200) >>> phiarr_fine = np.linspace(0, 2 * np.pi, 200) >>> zdata_fine = rsbs(thetaarr_fine, phiarr_fine)最後,我們將 coarsly-sampled 輸入數據與 finely-sampled 插值數據一起繪製,以檢查它們是否一致。
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(1, 2, 1) >>> ax2 = fig.add_subplot(1, 2, 2) >>> ax1.imshow(zdata) >>> ax2.imshow(zdata_fine) >>> plt.show()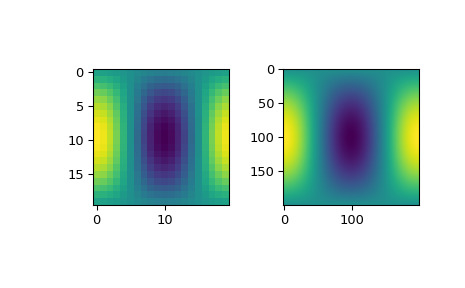
相關用法
- Python SciPy RectSphereBivariateSpline.ev用法及代碼示例
- Python SciPy RectBivariateSpline.__call__用法及代碼示例
- Python SciPy RectBivariateSpline.ev用法及代碼示例
- Python SciPy RealData.set_meta用法及代碼示例
- Python SciPy RegularGridInterpolator.__call__用法及代碼示例
- Python SciPy RelativeRiskResult.confidence_interval用法及代碼示例
- Python SciPy Rotation.from_matrix用法及代碼示例
- Python SciPy Rotation.__pow__用法及代碼示例
- Python SciPy Rotation.magnitude用法及代碼示例
- Python SciPy Rotation.as_matrix用法及代碼示例
- Python SciPy Rotation.as_euler用法及代碼示例
- Python SciPy Rotation.approx_equal用法及代碼示例
- Python SciPy Rotation.from_quat用法及代碼示例
- Python SciPy Rotation.as_mrp用法及代碼示例
- Python SciPy Rotation.from_mrp用法及代碼示例
- Python SciPy Rotation.__getitem__用法及代碼示例
- Python SciPy Rotation.from_rotvec用法及代碼示例
- Python SciPy Rotation.as_quat用法及代碼示例
- Python SciPy Rotation.__mul__用法及代碼示例
- Python SciPy Rotation.as_rotvec用法及代碼示例
- Python SciPy Rotation.apply用法及代碼示例
- Python SciPy Rotation.align_vectors用法及代碼示例
- Python SciPy Rotation.inv用法及代碼示例
- Python SciPy Rotation.random用法及代碼示例
- Python SciPy Rotation.from_euler用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.interpolate.RectSphereBivariateSpline.__call__。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
