sklearn例程:多分類輸出概率

示例簡介

本示例介紹如何繪製不同分類器的分類概率。我們在擁有3個類別的數據集上，使用如下分類模型進行多分類：

支持向量分類器(SVM Classification, 簡稱SVC)
- 線性SVC在默認情況下不是概率分類器，但在此示例中啟用了內置校準選項(probability=True)
邏輯回歸(LogisticRegression，簡稱LR)，嘗試了3種參數配置：
- 采用L1正則化
- 采用L2正則化和One-Vs-Rest模式，One-Vs-Rest簡稱OvR，即做多分類時，將1個類的樣本作為正例，其他類的樣本作為負例。
  - 使用One-Vs-Rest的邏輯回歸不是開箱即用的多類分類器。在下文中可用看到，與其他模型估計量相比，在將第2類和第3類分離時會有一些問題。
- 采用L2正則化和multinomial模式，multinomial即直接做多分類。
高斯過程分類（GaussianProcessClassifier，簡稱GPC）。

代碼實現[Python]


# -*- coding: utf-8 -*- 
print(__doc__)

# Author: Alexandre Gramfort 
# License: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:, 0:2]  # we only take the first two features for visualization
y = iris.target

n_features = X.shape[1]

C = 10
kernel = 1.0 * RBF([1.0, 1.0])  # for GPC

# 創建5個不同的分類器.
classifiers = {
    'L1 logistic': LogisticRegression(C=C, penalty='l1',
                                      solver='saga',
                                      multi_class='multinomial',
                                      max_iter=10000),
    'L2 logistic (Multinomial)': LogisticRegression(C=C, penalty='l2',
                                                    solver='saga',
                                                    multi_class='multinomial',
                                                    max_iter=10000),
    'L2 logistic (OvR)': LogisticRegression(C=C, penalty='l2',
                                            solver='saga',
                                            multi_class='ovr',
                                            max_iter=10000),
    'Linear SVC': SVC(kernel='linear', C=C, probability=True,
                      random_state=0),
    'GPC': GaussianProcessClassifier(kernel)
}

n_classifiers = len(classifiers)

plt.figure(figsize=(3 * 2, n_classifiers * 2))
plt.subplots_adjust(bottom=.2, top=.95)

xx = np.linspace(3, 9, 100)
yy = np.linspace(1, 5, 100).T
xx, yy = np.meshgrid(xx, yy)
Xfull = np.c_[xx.ravel(), yy.ravel()]

for index, (name, classifier) in enumerate(classifiers.items()):
    classifier.fit(X, y)

    y_pred = classifier.predict(X)
    accuracy = accuracy_score(y, y_pred)
    print("Accuracy (train) for %s: %0.1f%% " % (name, accuracy * 100))

    # View probabilities:
    probas = classifier.predict_proba(Xfull)
    n_classes = np.unique(y_pred).size
    for k in range(n_classes):
        plt.subplot(n_classifiers, n_classes, index * n_classes + k + 1)
        plt.title("Class %d" % k)
        if k == 0:
            plt.ylabel(name)
        imshow_handle = plt.imshow(probas[:, k].reshape((100, 100)),
                                   extent=(3, 9, 1, 5), origin='lower')
        plt.xticks(())
        plt.yticks(())
        idx = (y_pred == k)
        if idx.any():
            plt.scatter(X[idx, 0], X[idx, 1], marker='o', c='w', edgecolor='k')

ax = plt.axes([0.15, 0.04, 0.7, 0.05])
plt.title("Probability")
plt.colorbar(imshow_handle, cax=ax, orientation='horizontal')

plt.show()

代碼執行

代碼運行時間大約:0分1.409秒。
運行代碼輸出的文本內容如下，如上文所述OvR的LR不是天然的多分類器，所以效果相對較差。

Accuracy (train) for L1 logistic: 83.3%
Accuracy (train) for L2 logistic (Multinomial): 82.7%
Accuracy (train) for L2 logistic (OvR): 79.3%
Accuracy (train) for Linear SVC: 82.0%
Accuracy (train) for GPC: 82.7%

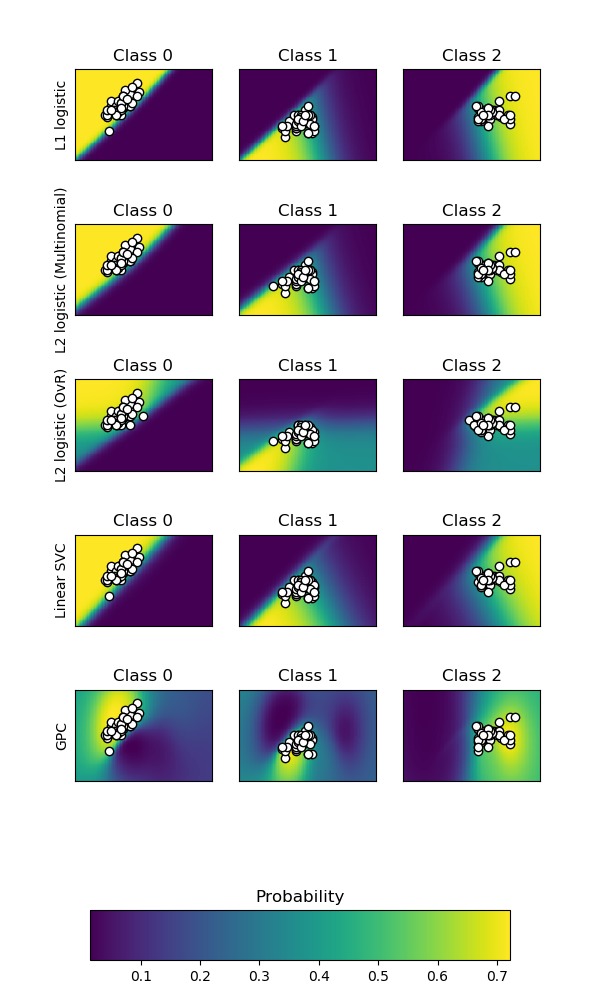
運行代碼輸出的圖片內容如下，圖中白色圓點表示樣本，背景色的深淺表示概率的強度(見最後一張圖，顏色越淺(黃)概率越大，顏色越深(深藍)概率越小)。我們再次可以看到，對於OvR的邏輯回歸，效果不太好——Class 1和Class 2的樣本對應的概率強度比較低！

Plot classification probability