示例簡介
本示例對比介紹了模型複雜度如何影響預測準確性和計算性能。
數據集是:波士頓住房數據集(Boston Housing dataset)用於回歸,20個新聞組數據集( 20 Newsgroups dataset)用於分類。
這裏,對比了多個分類和回歸模型,對於每類模型,我們通過選擇相關的模型參數來使模型的複雜性發生變化,
並測量對計算性能(延遲)和預測能力(MSE或漢明損失)的影響。
代碼實現[Python]
# -*- coding: utf-8 -*-
print(__doc__)
# Author: Eustache Diemert
# License: BSD 3 clause
import time
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.parasite_axes import host_subplot
from mpl_toolkits.axisartist.axislines import Axes
from scipy.sparse.csr import csr_matrix
from sklearn import datasets
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
from sklearn.svm.classes import NuSVR
from sklearn.ensemble.gradient_boosting import GradientBoostingRegressor
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.metrics import hamming_loss
# #############################################################################
# 函數
# 初始化隨機數生成器
np.random.seed(0)
# 生成用於分類和回歸的數據集
def generate_data(case, sparse=False):
"""Generate regression/classification data."""
bunch = None
if case == 'regression':
bunch = datasets.load_boston()
elif case == 'classification':
bunch = datasets.fetch_20newsgroups_vectorized(subset='all')
X, y = shuffle(bunch.data, bunch.target)
offset = int(X.shape[0] * 0.8)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]
if sparse:
X_train = csr_matrix(X_train)
X_test = csr_matrix(X_test)
else:
X_train = np.array(X_train)
X_test = np.array(X_test)
y_test = np.array(y_test)
y_train = np.array(y_train)
data = {'X_train': X_train, 'X_test': X_test, 'y_train': y_train,
'y_test': y_test}
return data
# 評估影響
def benchmark_influence(conf):
"""
Benchmark influence of :changing_param: on both MSE and latency.
"""
prediction_times = []
prediction_powers = []
complexities = []
for param_value in conf['changing_param_values']:
conf['tuned_params'][conf['changing_param']] = param_value
estimator = conf['estimator'](**conf['tuned_params'])
print("Benchmarking %s" % estimator)
estimator.fit(conf['data']['X_train'], conf['data']['y_train'])
conf['postfit_hook'](estimator)
complexity = conf['complexity_computer'](estimator)
complexities.append(complexity)
start_time = time.time()
for _ in range(conf['n_samples']):
y_pred = estimator.predict(conf['data']['X_test'])
elapsed_time = (time.time() - start_time) / float(conf['n_samples'])
prediction_times.append(elapsed_time)
pred_score = conf['prediction_performance_computer'](
conf['data']['y_test'], y_pred)
prediction_powers.append(pred_score)
print("Complexity: %d | %s: %.4f | Pred. Time: %fs\n" % (
complexity, conf['prediction_performance_label'], pred_score,
elapsed_time))
return prediction_powers, prediction_times, complexities
# 繪製影響
def plot_influence(conf, mse_values, prediction_times, complexities):
"""
Plot influence of model complexity on both accuracy and latency.
"""
plt.figure(figsize=(12, 6))
host = host_subplot(111, axes_class=Axes)
plt.subplots_adjust(right=0.75)
par1 = host.twinx()
host.set_xlabel('Model Complexity (%s)' % conf['complexity_label'])
y1_label = conf['prediction_performance_label']
y2_label = "Time (s)"
host.set_ylabel(y1_label)
par1.set_ylabel(y2_label)
p1, = host.plot(complexities, mse_values, 'b-', label="prediction error")
p2, = par1.plot(complexities, prediction_times, 'r-',
label="latency")
host.legend(loc='upper right')
host.axis["left"].label.set_color(p1.get_color())
par1.axis["right"].label.set_color(p2.get_color())
plt.title('Influence of Model Complexity - %s' % conf['estimator'].__name__)
plt.show()
# 統計模型非零參數
def _count_nonzero_coefficients(estimator):
a = estimator.coef_.toarray()
return np.count_nonzero(a)
# #############################################################################
# 主程
regression_data = generate_data('regression')
classification_data = generate_data('classification', sparse=True)
configurations = [
{'estimator': SGDClassifier,
'tuned_params': {'penalty': 'elasticnet', 'alpha': 0.001, 'loss':
'modified_huber', 'fit_intercept': True, 'tol': 1e-3},
'changing_param': 'l1_ratio',
'changing_param_values': [0.25, 0.5, 0.75, 0.9],
'complexity_label': 'non_zero coefficients',
'complexity_computer': _count_nonzero_coefficients,
'prediction_performance_computer': hamming_loss,
'prediction_performance_label': 'Hamming Loss (Misclassification Ratio)',
'postfit_hook': lambda x: x.sparsify(),
'data': classification_data,
'n_samples': 30},
{'estimator': NuSVR,
'tuned_params': {'C': 1e3, 'gamma': 2 ** -15},
'changing_param': 'nu',
'changing_param_values': [0.1, 0.25, 0.5, 0.75, 0.9],
'complexity_label': 'n_support_vectors',
'complexity_computer': lambda x: len(x.support_vectors_),
'data': regression_data,
'postfit_hook': lambda x: x,
'prediction_performance_computer': mean_squared_error,
'prediction_performance_label': 'MSE',
'n_samples': 30},
{'estimator': GradientBoostingRegressor,
'tuned_params': {'loss': 'ls'},
'changing_param': 'n_estimators',
'changing_param_values': [10, 50, 100, 200, 500],
'complexity_label': 'n_trees',
'complexity_computer': lambda x: x.n_estimators,
'data': regression_data,
'postfit_hook': lambda x: x,
'prediction_performance_computer': mean_squared_error,
'prediction_performance_label': 'MSE',
'n_samples': 30},
]
for conf in configurations:
prediction_performances, prediction_times, complexities = \
benchmark_influence(conf)
plot_influence(conf, prediction_performances, prediction_times,
complexities)
代碼執行
代碼運行時間大約:0分35.625秒。
運行代碼輸出的文本內容如下:
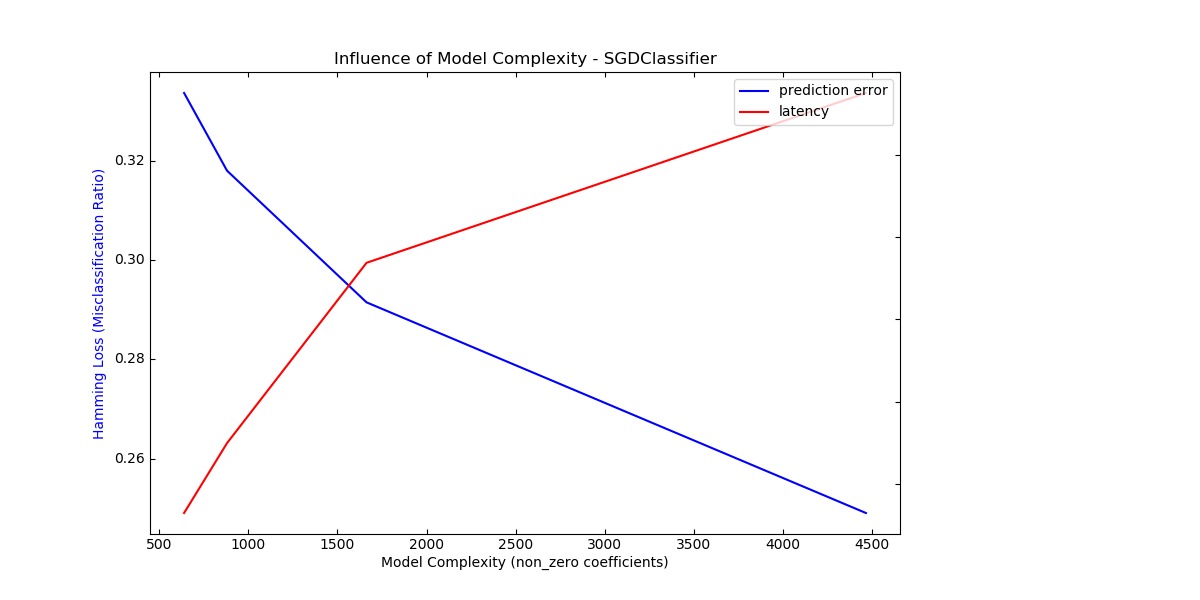
Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.25, loss='modified_huber',
penalty='elasticnet')
Complexity: 4466 | Hamming Loss (Misclassification Ratio): 0.2491 | Pred. Time: 0.021496s
Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.5, loss='modified_huber',
penalty='elasticnet')
Complexity: 1663 | Hamming Loss (Misclassification Ratio): 0.2915 | Pred. Time: 0.017370s
Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.75, loss='modified_huber',
penalty='elasticnet')
Complexity: 880 | Hamming Loss (Misclassification Ratio): 0.3180 | Pred. Time: 0.012989s
Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.9, loss='modified_huber',
penalty='elasticnet')
Complexity: 639 | Hamming Loss (Misclassification Ratio): 0.3337 | Pred. Time: 0.011292s
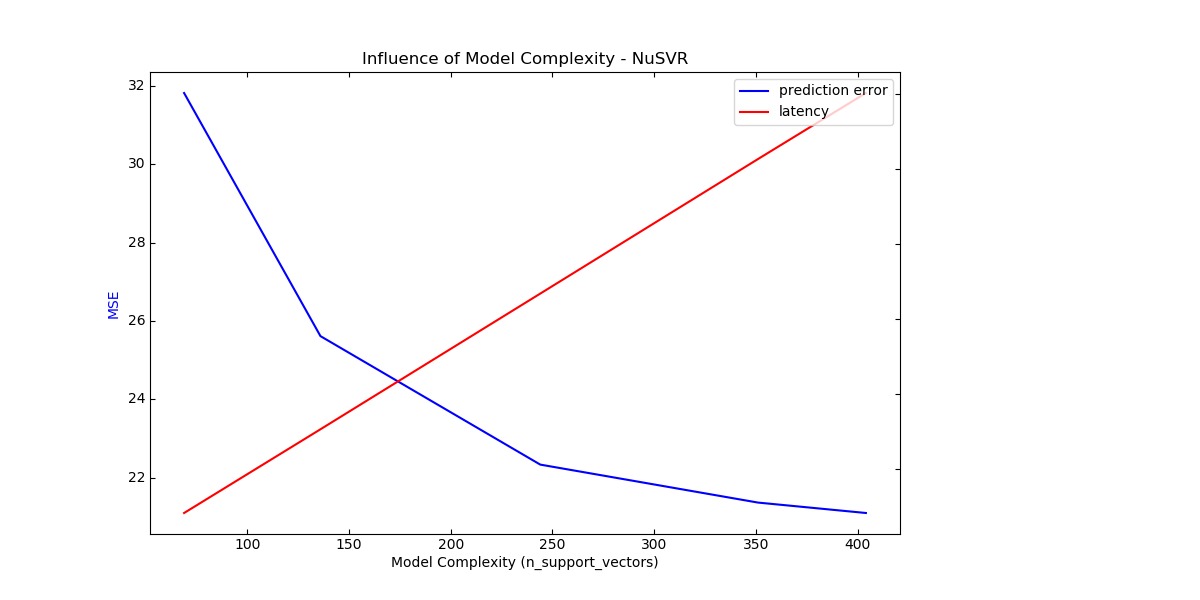
Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.1)
Complexity: 69 | MSE: 31.8139 | Pred. Time: 0.000283s
Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.25)
Complexity: 136 | MSE: 25.6140 | Pred. Time: 0.000506s
Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05)
Complexity: 244 | MSE: 22.3375 | Pred. Time: 0.000868s
Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.75)
Complexity: 351 | MSE: 21.3688 | Pred. Time: 0.001226s
Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.9)
Complexity: 404 | MSE: 21.1033 | Pred. Time: 0.001402s
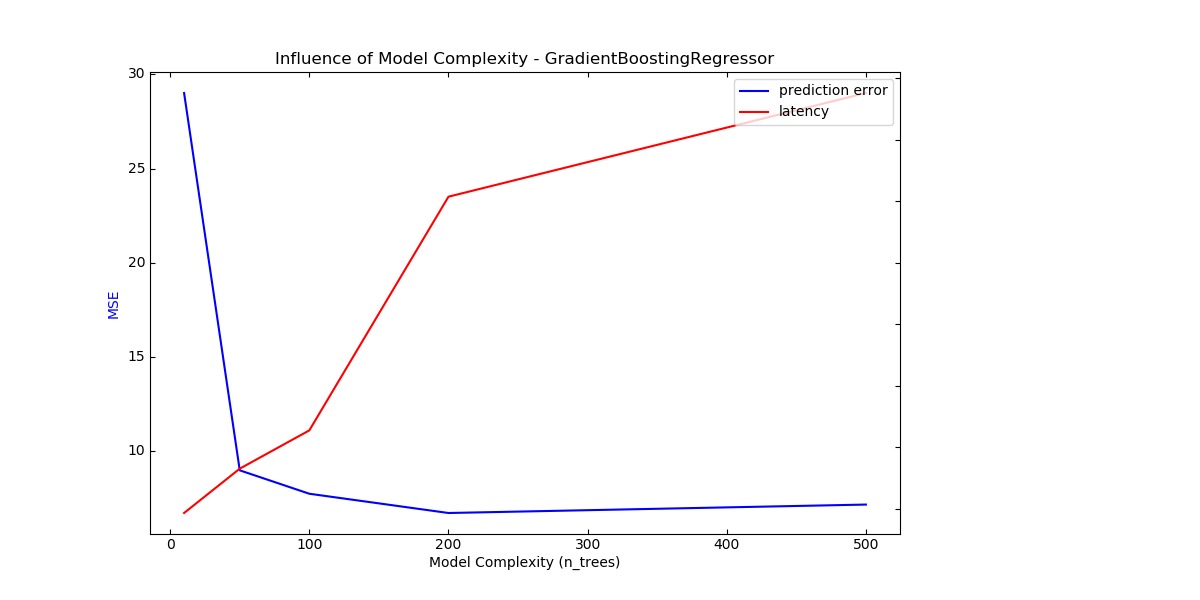
Benchmarking GradientBoostingRegressor(n_estimators=10)
Complexity: 10 | MSE: 29.0148 | Pred. Time: 0.000093s
Benchmarking GradientBoostingRegressor(n_estimators=50)
Complexity: 50 | MSE: 8.9630 | Pred. Time: 0.000165s
Benchmarking GradientBoostingRegressor()
Complexity: 100 | MSE: 7.7187 | Pred. Time: 0.000227s
Benchmarking GradientBoostingRegressor(n_estimators=200)
Complexity: 200 | MSE: 6.6955 | Pred. Time: 0.000608s
Benchmarking GradientBoostingRegressor(n_estimators=500)
Complexity: 500 | MSE: 7.1437 | Pred. Time: 0.000776s
運行代碼輸出的圖片內容如下:
源碼下載
- Python版源碼文件: plot_model_complexity_influence.py
- Jupyter Notebook版源碼文件: plot_model_complexity_influence.ipynb
