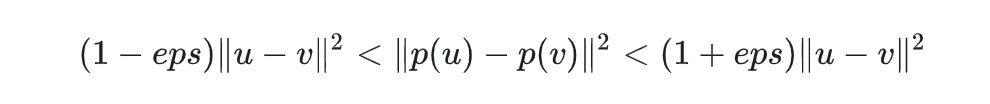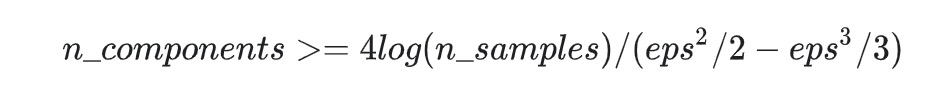sklearn例程:隨機投影嵌入(Embedding)的Johnson-Lindenstrauss界限

Johnson-Lindenstrauss綁定為帶有隨機投影的嵌入簡介

Johnson-Lindenstrauss引理（簡稱JL引理）指出，任何高維數據集都可以隨機投影到低維歐氏空間中，同時控製點的兩兩距離的失真度。也就說將點從高維空間映射到低維空間之後，新舊空間點的距離是可以近似相等的。

理論界限

隨機投影引起的失真度p，如下式所示：

其中u和v是從大小為[n_samples，n_features]的數據集中獲取的任意行，而p是形狀為[n_components，n_features](或稀疏Achlioptas矩陣)的隨機高斯N(0，1)矩陣的投影。

保證eps-embedding的最小組件數量為：

注：見後文代碼執行的圖，

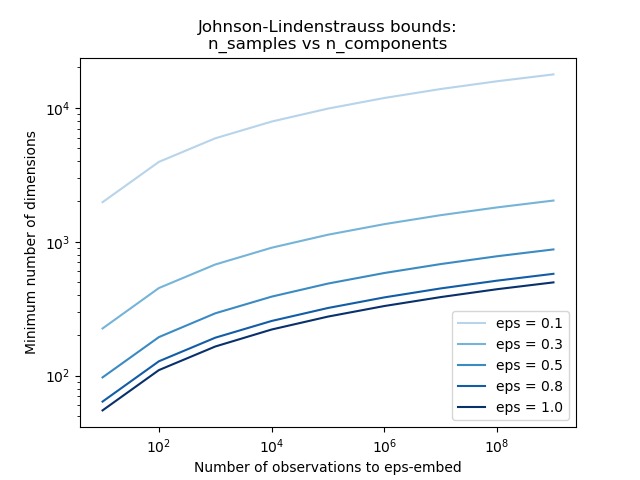
第一個圖顯示隨著樣本數量n_samples的增加，最小尺寸n_components對數增加以保證eps-embedding。
第二個圖顯示了對於給定數量的樣本n_samples，容許失真的增加eps可以大幅減少最小維度n_components

實證驗證

我們在手寫數字數據集或20個新聞組文本文檔(TF-IDF詞頻)數據集上驗證上述界限：

對於手寫數字數據集，將500張手寫數字圖片的一些8×8灰度像素數據隨機投影到各種較大維度n_components的空間。
對於20個新聞組數據集，使用稀疏隨機矩陣將總共500個具有10萬個特征的文檔投影到較小的歐幾裏得空間，並為目標維數n_components設置不同的值。

示例中默認數據集是數字數據集。要在二十個新聞組數據集上運行該示例，請將–twenty-newsgroups命令行參數傳遞給此腳本。

對於每個值n_components，我們繪製：

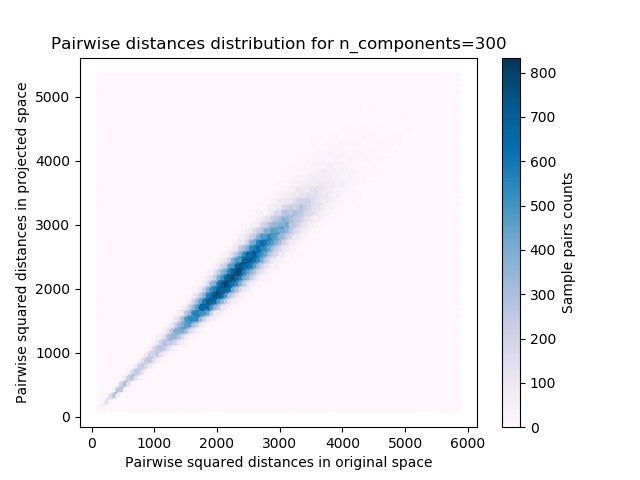
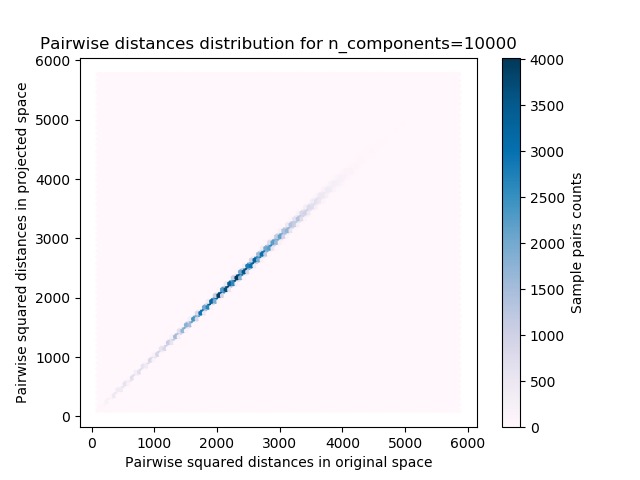
原始空間和投影空間中成對距離的樣本對的2D分布(2D分別為x和y軸)。
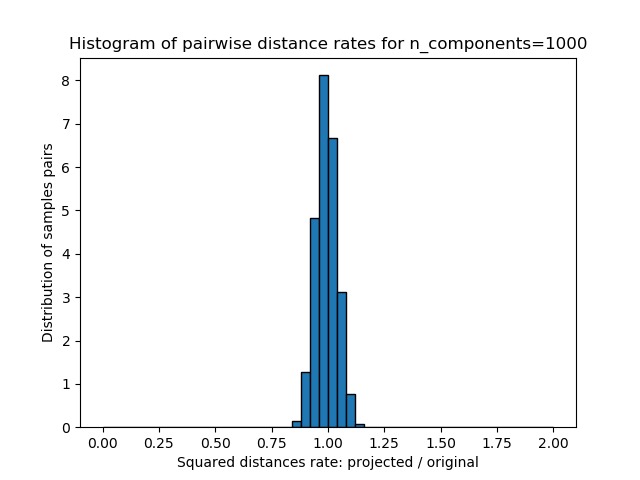
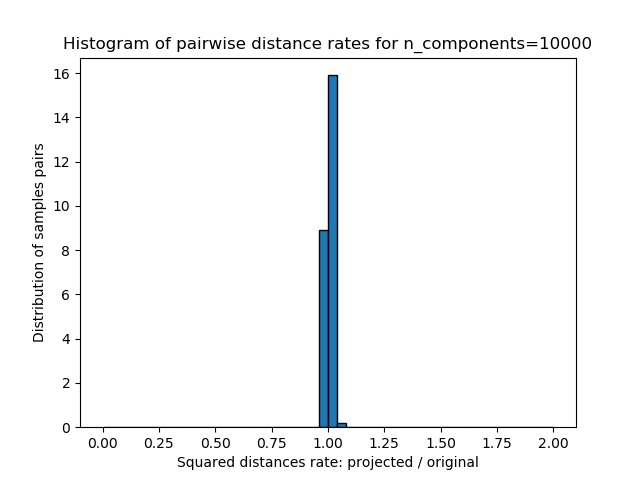
這些距離的比例的一維直方圖(投影/原始)。

我們可以看到，對於較小的n_components，分布較寬，有許多扭曲的對和偏斜的分布(由於左側的零比率的硬性限製，因為距離始終為正值)；而對於較大的n_components值，則可以控製失真，並且通過隨機投影可以很好地保留距離。

備注

根據JL引理，無論原始數據集的特征數量如何，投影500個樣本而不會產生太多失真都將至少需要數千個維度。

因此，對在輸入空間中僅具有64個特征的數字數據集使用隨機投影是沒有意義的：在這種情況下，它不允許降維。所以在這個手寫數字數據集上我們實驗用的是增加維度。而另一方麵，在二十個新聞組數據集中，維數可以從56436降低到10000，同時合理地保持點對的距離。

代碼實現[Python]


# -*- coding: utf-8 -*- 
print(__doc__)

import sys
from time import time
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from distutils.version import LooseVersion
from sklearn.random_projection import johnson_lindenstrauss_min_dim
from sklearn.random_projection import SparseRandomProjection
from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.datasets import load_digits
from sklearn.metrics.pairwise import euclidean_distances

# `normed` is being deprecated in favor of `density` in histograms
if LooseVersion(matplotlib.__version__) >= '2.1':
    density_param = {'density': True}
else:
    density_param = {'normed': True}

# Part 1: 繪製n_components_min和n_samples之間的理論依賴性

# 容許失真的範圍
eps_range = np.linspace(0.1, 0.99, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(eps_range)))

# range of number of samples (observation) to embed
n_samples_range = np.logspace(1, 9, 9)

plt.figure()
for eps, color in zip(eps_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples_range, eps=eps)
    plt.loglog(n_samples_range, min_n_components, color=color)

plt.legend(["eps = %0.1f" % eps for eps in eps_range], loc="lower right")
plt.xlabel("Number of observations to eps-embed")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_samples vs n_components")

# 容許失真的範圍
eps_range = np.linspace(0.01, 0.99, 100)

# range of number of samples (observation) to embed
n_samples_range = np.logspace(2, 6, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(n_samples_range)))

plt.figure()
for n_samples, color in zip(n_samples_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples, eps=eps_range)
    plt.semilogy(eps_range, min_n_components, color=color)

plt.legend(["n_samples = %d" % n for n in n_samples_range], loc="upper right")
plt.xlabel("Distortion eps")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_components vs eps")


# Part 2: 對維數很低且密度高的某些數字圖像或對維數高且稀疏的20個新聞組數據集執行稀疏隨機投影
if '--twenty-newsgroups' in sys.argv:
    # Need an internet connection hence not enabled by default
    data = fetch_20newsgroups_vectorized().data[:500]
else:
    data = load_digits().data[:500]

n_samples, n_features = data.shape
print("Embedding %d samples with dim %d using various random projections"
      % (n_samples, n_features))

n_components_range = np.array([300, 1000, 10000])
dists = euclidean_distances(data, squared=True).ravel()

# 僅選擇不相同的樣本對
nonzero = dists != 0
dists = dists[nonzero]

for n_components in n_components_range:
    t0 = time()
    rp = SparseRandomProjection(n_components=n_components)
    projected_data = rp.fit_transform(data)
    print("Projected %d samples from %d to %d in %0.3fs"
          % (n_samples, n_features, n_components, time() - t0))
    if hasattr(rp, 'components_'):
        n_bytes = rp.components_.data.nbytes
        n_bytes += rp.components_.indices.nbytes
        print("Random matrix with size: %0.3fMB" % (n_bytes / 1e6))

    projected_dists = euclidean_distances(
        projected_data, squared=True).ravel()[nonzero]

    plt.figure()
    plt.hexbin(dists, projected_dists, gridsize=100, cmap=plt.cm.PuBu)
    plt.xlabel("Pairwise squared distances in original space")
    plt.ylabel("Pairwise squared distances in projected space")
    plt.title("Pairwise distances distribution for n_components=%d" %
              n_components)
    cb = plt.colorbar()
    cb.set_label('Sample pairs counts')

    rates = projected_dists / dists
    print("Mean distances rate: %0.2f (%0.2f)"
          % (np.mean(rates), np.std(rates)))

    plt.figure()
    plt.hist(rates, bins=50, range=(0., 2.), edgecolor='k', **density_param)
    plt.xlabel("Squared distances rate: projected / original")
    plt.ylabel("Distribution of samples pairs")
    plt.title("Histogram of pairwise distance rates for n_components=%d" %
              n_components)

    # TODO: compute the expected value of eps and add them to the previous plot
    # as vertical lines / region

plt.show()

代碼執行

代碼運行時間大約:0分1.837秒。
運行代碼輸出的文本內容如下:

Embedding 500 samples with dim 64 using various random projections
Projected 500 samples from 64 to 300 in 0.016s
Random matrix with size: 0.028MB
Mean distances rate: 0.97 (0.08)
Projected 500 samples from 64 to 1000 in 0.048s
Random matrix with size: 0.096MB
Mean distances rate: 0.99 (0.05)
Projected 500 samples from 64 to 10000 in 0.594s
Random matrix with size: 0.964MB
Mean distances rate: 1.01 (0.01)

運行代碼輸出的圖片內容如下:

The Johnson-Lindenstrauss bound for embedding with random projections