sklearn例程:核嶺回歸與SVM回歸的比較

核嶺回歸與SVM回歸的比較簡介

核嶺回歸(KRR)和SVM回歸(SVR)都是通過采用核技巧來學習非線性函數。也就是說，二者在由核產生的空間中學習了一個線性函數，這個函數與原始空間中的非線性函數相對應。它們的損失函數是不同的(嶺損失 VS epsilon鬆弛損失)。與SVR相比，KRR能以閉式解完成的擬合，所以對於中等規模的數據集通常更快。不過，KRR學習的模型是非稀疏的，因此在預測時比產生稀疏解的SVR要慢。

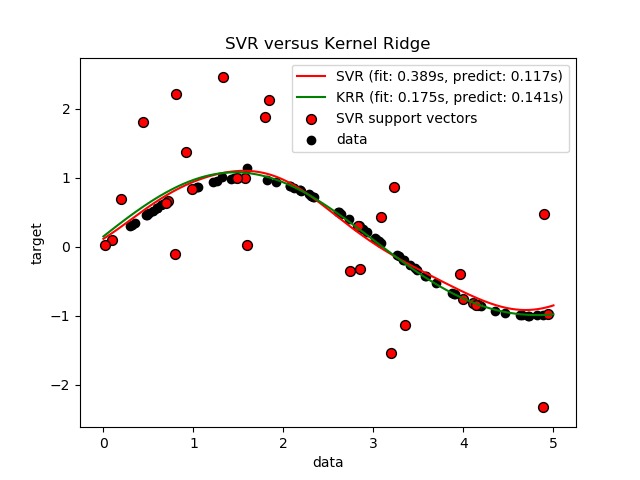
此示例介紹了人工數據集上的兩種方法，該方法由正弦目標函數和添加到每五個數據點的強噪聲組成。下文中的第一張圖比較了KRR和SVR學習到的模型，其中複雜度/正則化和RBF核的帶寬都使用了網格搜索(grid-search)優化。可以看到，學到的函數非常相似；不過，擬合KRR大約比擬合SVR快7倍(兩者均使用grid-search)。但是，使用SVR對100000個目標值做預測時的速度比KRR快了3倍以上，因為它僅使用了100個訓練數據點的約1/3就學會了稀疏模型(作為支持向量)。

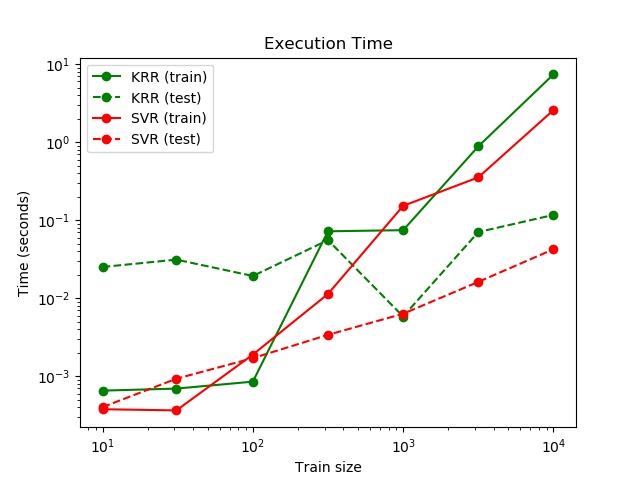
從示例代碼輸出的圖片可以看到(見下文)，不同大小的訓練集的KRR和SVR的擬合和預測時間的對比情況。對於中等規模的訓練集(少於1000個樣本)，擬合KRR比SVR更快。但是，對於較大的訓練集，SVR的擴展性更好。關於預測時間，由於SVR學到的是稀疏解決方案，對於所有規模的訓練集，SVR均比KRR更快。請注意，稀疏程度以及預測時間取決於SVR的參數epsilon和C。

代碼實現[Python]


# -*- coding: utf-8 -*- 

# Authors: Jan Hendrik Metzen 
# License: BSD 3 clause


import time

import numpy as np

from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import learning_curve
from sklearn.kernel_ridge import KernelRidge
import matplotlib.pyplot as plt

rng = np.random.RandomState(0)

# #############################################################################
# 生成樣本數據
X = 5 * rng.rand(10000, 1)
y = np.sin(X).ravel()

# Add noise to targets
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))

X_plot = np.linspace(0, 5, 100000)[:, None]

# #############################################################################
# 擬合回歸模型
train_size = 100
svr = GridSearchCV(SVR(kernel='rbf', gamma=0.1), cv=5,
                   param_grid={"C": [1e0, 1e1, 1e2, 1e3],
                               "gamma": np.logspace(-2, 2, 5)})

kr = GridSearchCV(KernelRidge(kernel='rbf', gamma=0.1), cv=5,
                  param_grid={"alpha": [1e0, 0.1, 1e-2, 1e-3],
                              "gamma": np.logspace(-2, 2, 5)})

t0 = time.time()
svr.fit(X[:train_size], y[:train_size])
svr_fit = time.time() - t0
print("SVR complexity and bandwidth selected and model fitted in %.3f s"
      % svr_fit)

t0 = time.time()
kr.fit(X[:train_size], y[:train_size])
kr_fit = time.time() - t0
print("KRR complexity and bandwidth selected and model fitted in %.3f s"
      % kr_fit)

sv_ratio = svr.best_estimator_.support_.shape[0] / train_size
print("Support vector ratio: %.3f" % sv_ratio)

t0 = time.time()
y_svr = svr.predict(X_plot)
svr_predict = time.time() - t0
print("SVR prediction for %d inputs in %.3f s"
      % (X_plot.shape[0], svr_predict))

t0 = time.time()
y_kr = kr.predict(X_plot)
kr_predict = time.time() - t0
print("KRR prediction for %d inputs in %.3f s"
      % (X_plot.shape[0], kr_predict))


# #############################################################################
# 結果可視化
sv_ind = svr.best_estimator_.support_
plt.scatter(X[sv_ind], y[sv_ind], c='r', s=50, label='SVR support vectors',
            zorder=2, edgecolors=(0, 0, 0))
plt.scatter(X[:100], y[:100], c='k', label='data', zorder=1,
            edgecolors=(0, 0, 0))
plt.plot(X_plot, y_svr, c='r',
         label='SVR (fit: %.3fs, predict: %.3fs)' % (svr_fit, svr_predict))
plt.plot(X_plot, y_kr, c='g',
         label='KRR (fit: %.3fs, predict: %.3fs)' % (kr_fit, kr_predict))
plt.xlabel('data')
plt.ylabel('target')
plt.title('SVR versus Kernel Ridge')
plt.legend()

# 可視化訓練和預測時間
plt.figure()

# 生成樣本數據
X = 5 * rng.rand(10000, 1)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))
sizes = np.logspace(1, 4, 7).astype(np.int)
for name, estimator in {"KRR": KernelRidge(kernel='rbf', alpha=0.1,
                                           gamma=10),
                        "SVR": SVR(kernel='rbf', C=1e1, gamma=10)}.items():
    train_time = []
    test_time = []
    for train_test_size in sizes:
        t0 = time.time()
        estimator.fit(X[:train_test_size], y[:train_test_size])
        train_time.append(time.time() - t0)

        t0 = time.time()
        estimator.predict(X_plot[:1000])
        test_time.append(time.time() - t0)

    plt.plot(sizes, train_time, 'o-', color="r" if name == "SVR" else "g",
             label="%s (train)" % name)
    plt.plot(sizes, test_time, 'o--', color="r" if name == "SVR" else "g",
             label="%s (test)" % name)

plt.xscale("log")
plt.yscale("log")
plt.xlabel("Train size")
plt.ylabel("Time (seconds)")
plt.title('Execution Time')
plt.legend(loc="best")

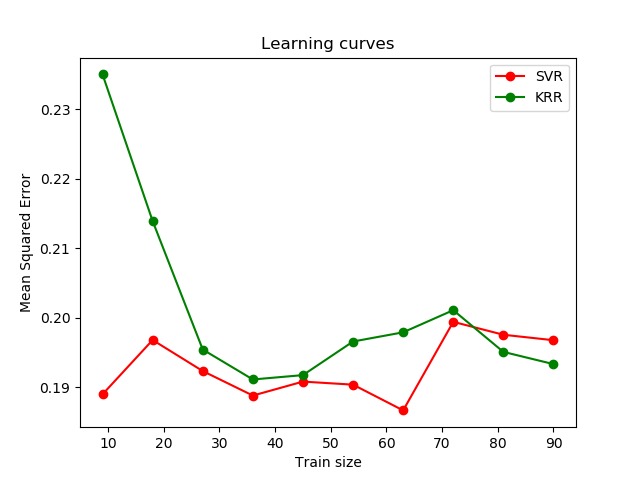
# 可視化學習曲線
plt.figure()

svr = SVR(kernel='rbf', C=1e1, gamma=0.1)
kr = KernelRidge(kernel='rbf', alpha=0.1, gamma=0.1)
train_sizes, train_scores_svr, test_scores_svr = \
    learning_curve(svr, X[:100], y[:100], train_sizes=np.linspace(0.1, 1, 10),
                   scoring="neg_mean_squared_error", cv=10)
train_sizes_abs, train_scores_kr, test_scores_kr = \
    learning_curve(kr, X[:100], y[:100], train_sizes=np.linspace(0.1, 1, 10),
                   scoring="neg_mean_squared_error", cv=10)

plt.plot(train_sizes, -test_scores_svr.mean(1), 'o-', color="r",
         label="SVR")
plt.plot(train_sizes, -test_scores_kr.mean(1), 'o-', color="g",
         label="KRR")
plt.xlabel("Train size")
plt.ylabel("Mean Squared Error")
plt.title('Learning curves')
plt.legend(loc="best")

plt.show()

代碼執行

代碼運行時間大約:0分13.067秒。
運行代碼輸出的文本內容如下:

SVR complexity and bandwidth selected and model fitted in 0.389 s
KRR complexity and bandwidth selected and model fitted in 0.175 s
Support vector ratio: 0.320
SVR prediction for 100000 inputs in 0.117 s
KRR prediction for 100000 inputs in 0.141 s

運行代碼輸出的圖片內容如下:

Comparison of kernel ridge regression and SVR