本文简要介绍 python 语言中scipy.interpolate.SmoothSphereBivariateSpline.__call__的用法。
用法:
SmoothSphereBivariateSpline.__call__(theta, phi, dtheta=0, dphi=0, grid=True)#评估给定位置处的样条曲线或其导数。
- theta, phi: array_like
输入坐标。
如果网格为 False,在点处评估样条线
(theta[i], phi[i]), i=0, ..., len(x)-1。遵循标准 Numpy 广播。如果网格为 True:在由坐标数组 theta、phi 定义的网格点处计算样条线。数组必须按升序排序。轴的顺序与
np.meshgrid(..., indexing="ij")并且与默认排序不一致np.meshgrid(..., indexing="xy").- dtheta: 整数,可选
theta-derivative的订单
- dphi: int
phi-derivative的订单
- grid: bool
是否在输入数组跨越的网格上或在输入数组指定的点上评估结果。
参数 ::
例子:
假设我们要使用样条线在球体上插值二元函数。该函数的值在经度和纬度网格上已知。
>>> import numpy as np >>> from scipy.interpolate import RectSphereBivariateSpline >>> def f(theta, phi): ... return np.sin(theta) * np.cos(phi)我们评估网格上的函数。请注意,网格网格的默认索引 =”xy” 会导致插值后出现意外(转置)结果。
>>> thetaarr = np.linspace(0, np.pi, 22)[1:-1] >>> phiarr = np.linspace(0, 2 * np.pi, 21)[:-1] >>> thetagrid, phigrid = np.meshgrid(thetaarr, phiarr, indexing="ij") >>> zdata = f(thetagrid, phigrid)接下来我们设置插值器并使用它在更精细的网格上评估函数。
>>> rsbs = RectSphereBivariateSpline(thetaarr, phiarr, zdata) >>> thetaarr_fine = np.linspace(0, np.pi, 200) >>> phiarr_fine = np.linspace(0, 2 * np.pi, 200) >>> zdata_fine = rsbs(thetaarr_fine, phiarr_fine)最后,我们将 coarsly-sampled 输入数据与 finely-sampled 插值数据一起绘制,以检查它们是否一致。
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(1, 2, 1) >>> ax2 = fig.add_subplot(1, 2, 2) >>> ax1.imshow(zdata) >>> ax2.imshow(zdata_fine) >>> plt.show()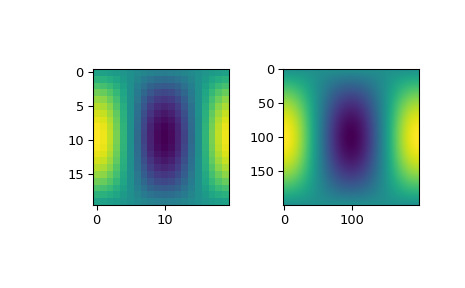
相关用法
- Python SciPy SmoothSphereBivariateSpline.ev用法及代码示例
- Python SciPy SmoothBivariateSpline.__call__用法及代码示例
- Python SciPy SmoothBivariateSpline.ev用法及代码示例
- Python SciPy ShortTimeFFT.from_dual用法及代码示例
- Python SciPy ShortTimeFFT.from_window用法及代码示例
- Python SciPy SuperLU.perm_c用法及代码示例
- Python SciPy SuperLU.solve用法及代码示例
- Python SciPy ShortTimeFFT.istft用法及代码示例
- Python SciPy SuperLU.perm_r用法及代码示例
- Python SciPy ShortTimeFFT.spectrogram用法及代码示例
- Python SciPy interpolate.make_interp_spline用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy ClusterNode.pre_order用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy FortranFile.read_record用法及代码示例
- Python SciPy ndimage.correlate用法及代码示例
- Python SciPy special.exp1用法及代码示例
- Python SciPy special.expn用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy interpolate.krogh_interpolate用法及代码示例
- Python SciPy ndimage.morphological_gradient用法及代码示例
- Python SciPy distance.sokalmichener用法及代码示例
- Python SciPy linalg.eigvalsh_tridiagonal用法及代码示例
- Python SciPy linalg.cdf2rdf用法及代码示例
- Python SciPy csc_array.diagonal用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.interpolate.SmoothSphereBivariateSpline.__call__。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
