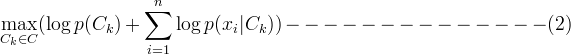下面是章节朴素贝叶斯的正文(其他内容参见全文目录)
朴素贝叶斯是一个简单的多分类算法。之所以称为朴素,是因为该算法假设特征之间相互独立。朴素贝叶斯的训练非常高效:通过一趟遍历训练数据,计算出每个特征对于给定标签的条件概率分布,然后应用贝叶斯定理计算标签对于观察值的条件概率分布,最后使用这个条件概率进行预测。
朴素贝叶斯算法易于求解的核心原理是:
1) 贝叶斯公式: p(x∩C)=p(x)*p(C|x)=p(C)*p(x|C), 即p(C|x) = p(C) * p(x|C)/p(x)
2)当特征相互独立的情况下,所有特征同时出现的概率等于每个特征出现的概率之乘积,即:
基于上述原理,朴素贝叶斯在分类问题可以用公式表达为:
其中Z = p(x)他的只依赖于x1, x2, …, xn,而不依赖于类型,即对所有类型来说,Z都是一样的,所以在实际计算中可以把这个省去。也就是说,朴素贝叶斯分类要解决的问题是:
即通过公式计算出每一类的权值,然后取取值最大的类作为预测结果。其中arg max f(Ck)表示使f(Ck)最大的Ck的值。
MLlib支持的是多项式朴素贝叶斯 ,该算法经常用于文档分类。为什么要用多项式朴的素贝叶斯?这是因为,当有大量特征的时候,就会有多个特征值(浮点数)相乘,一方面计算量大,另外也有浮点数溢出的风险。所以我们可以对公式(1)取对数,根据log(x *y) = log(x) + log(y), 我们可以得到:
公式(2)就是一个关于概率p(xi)的多项式。
在文档分类的应用场景中,观察值是文档的特征,每个特征值用词频表示。这样每个特征值>=0,对于特征值等于0的情况,需要做特殊处理,根据公式(1),由于是相乘,如果某个特征为0,那么,即使其他特征频数很大,最后结果也等于0。所以需要对特征的频度做特殊处理,常用的方法有Additive Smoothing(加法平滑,平滑参数λ=1.0)。文本分类中特征向量一般是稀疏的,所以可以使用SparseVector来利用这个稀疏性。另外由于训练数据只使用一次,所以不用缓存。
朴素贝叶斯实现了多项式贝叶斯。它以RDD[LabeledPoint]和平滑参数lambda作为输入,输出一个朴素贝叶斯模型 ,模型可用于评估和预测。示例如下:
from pyspark.mllib.classification import NaiveBayes
from pyspark.mllib.linalg import Vectors
from pyspark.mllib.regression import LabeledPoint
def parseLine(line):
parts = line.split(',')
label = float(parts[0])
features = Vectors.dense([float(x) for x in parts[1].split(' ')])
return LabeledPoint(label, features)
data = sc.textFile('data/mllib/sample_naive_bayes_data.txt').map(parseLine)
# Split data aproximately into training (60%) and test (40%)
training, test = data.randomSplit([0.6, 0.4], seed = 0)
# Train a naive Bayes model.
model = NaiveBayes.train(training, 1.0)
# Make prediction and test accuracy.
predictionAndLabel = test.map(lambda p : (model.predict(p.features), p.label))
accuracy = 1.0 * predictionAndLabel.filter(lambda (x, v): x == v).count() / test.count()