本文介绍Embedding的概念,给出了如何在TensorFlow中进行Embedding训练的简单示例,并解释了如何使用TensorBoard Embedding投影查看嵌入。前两部分是针对机器学习或TensorFlow的新手, Embedding投影如何做面向各级用户。
一个Embedding是从离散对象(如单词)到实数向量的映射。例如,英文单词(成千上万个)的300维Embedding可以包括:
blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259)
blues: (0.01396, 0.11887, -0.48963, ..., 0.033483, -0.10007, 0.1158)
orange: (-0.24776, -0.12359, 0.20986, ..., 0.079717, 0.23865, -0.014213)
oranges: (-0.35609, 0.21854, 0.080944, ..., -0.35413, 0.38511, -0.070976)
这些向量中的各个维度通常没有固有的意义。机器学习要利用的是向量之间的位置和距离的整体模式。
Embedding对于机器学习的输入非常重要。更普遍的分类器和神经网络,一般是对实数的向量起作用。他们最好是在密集向量上训练,向量中所有的值都有助于定义一个对象。然而,对于机器学习的许多重要的输入,例如文字,没有自然的矢量表示。Embedding函数是将这些离散输入对象转换为有用的连续向量的标准和有效的方法。
Embedding作为机器学习的输出也是有价值的。由于Embedding将对象映射到向量,因此应用程序可以使用向量空间中的相似性(例如,欧几里得距离或向量之间的角度)作为对象相似度的强大而灵活的度量。一个常见的用途是找到最近的邻居。例如,使用与上面相同的单词Embedding,这里是每个单词的三个最近的邻居和相应的角度:
blue: (red, 47.6°), (yellow, 51.9°), (purple, 52.4°)
blues: (jazz, 53.3°), (folk, 59.1°), (bluegrass, 60.6°)
orange: (yellow, 53.5°), (colored, 58.0°), (bright, 59.9°)
oranges: (apples, 45.3°), (lemons, 48.3°), (mangoes, 50.4°)
从上面可以看到,苹果和橙子在某种程度上比柠檬和橙子(相距45.3°)(相隔48.3°)更相似。
在TensorFlow Embedding
要在TensorFlow中创建词Embedding,我们首先将文本分成单词,然后为词汇表中的每个单词分配一个整数。让我们假设这已经完成了,word_ids是这些整数的一个向量。例如,“I have a cat.”这个句子可以被分成两部分[“I”, “have”, “a”, “cat”, “.”]然后相应的word_ids张量维度为[5],即由5个整数组成。为了将这些单词标识映射到向量,我们需要创建Embedding变量并使用tf.nn.embedding_lookup函数如下:
word_embeddings = tf.get_variable(“word_embeddings”,
[vocabulary_size, embedding_size])
embedded_word_ids = tf.nn.embedding_lookup(word_embeddings, word_ids)
之后,张量embedded_word_ids的维度是[5, embedding_size]在我们的例子中,包含5个单词中每一个的Embedding(密集向量)。在训练结束时,word_embeddings将包含词汇表中所有单词的Embedding。
Embedding可以使用许多网络类型训练,并且可以使用各种损失函数和数据集。例如,给定大量句子,可以使用递归神经网络来预测来自前一个单词的下一个单词,或者可以训练两个网络来做多语言翻译。这些方法在词的矢量表示教程中有介绍。
可视化Embedding
TensorBoard包括Embedding Projector(Embedding投影),这个工具可以让你交互式地显示Embedding。该工具可以读取模型中的Embedding,并在二维或三维中渲染它们。
Embedding投影有三个面板:
- 数据面板在左上方,您可以选择运行,Embedding变量和数据列,通过颜色标记点。
- 投影面板在左下方,您可以选择投影类型。
- 检查员面板在右侧,您可以在那里搜索特定点并查看最近的邻居列表。
投影
Embedding投影提供三种方法来降低数据集的维度。
-
t-SNE:一种非线性非确定性算法(T-distributed随机邻居Embedding),它试图在数据中保留局部邻域,这通常是以扭曲全局结构为代价的。您可以选择是否计算2维或3维投影。
-
PCA:线性确定算法(主成分分析),尽可能在尽可能少的维度上捕捉尽可能多的数据变化。 PCA往往会突出显示数据中的large-scale结构,但会扭曲本地邻域。Embedding投影计算前10个主要组件,从中您可以选择两个或三个查看。
-
自定义:在数据中使用标签指定水平和垂直轴上的线性投影。例如,通过为”Left”和”Right”提供文本模式来定义水平轴。Embedding投影查找标签与”Left”模式相匹配的所有点,并计算该组的质心;”Right”类似。穿过这两个质心的线定义了水平轴。垂直轴同样是根据与”Up”和”Down”文本模式匹配的点的质心来计算的。
其他有用的文章是如何有效地使用t-SNE和主成分分析直观解释。
浏览
您可以通过使用自然click-and-drag手势进行缩放,旋转和平移来做可视方化浏览。将鼠标悬停在某个点上会显示所有元数据。您也可以检查最近邻子集。点击一个点会导致右窗格列出最近的邻居,以及到当前点的距离。投影中还强调了最近邻的点。
将视图限制为点的子集并仅在这些点上执行投影有时是有用的。为此,您可以通过多种方式选择点:
- 点击一个点后,最近的邻居也被选中。
- 搜索后,选择与查询匹配的点。
- 启用选择,单击一个点并拖动定义一个选择范围。
然后点击“隔离NNN点”按钮,它位于左侧“检查器”窗格顶部,下图显示了101个被选中的点,可以让用户单击“隔离101点”:
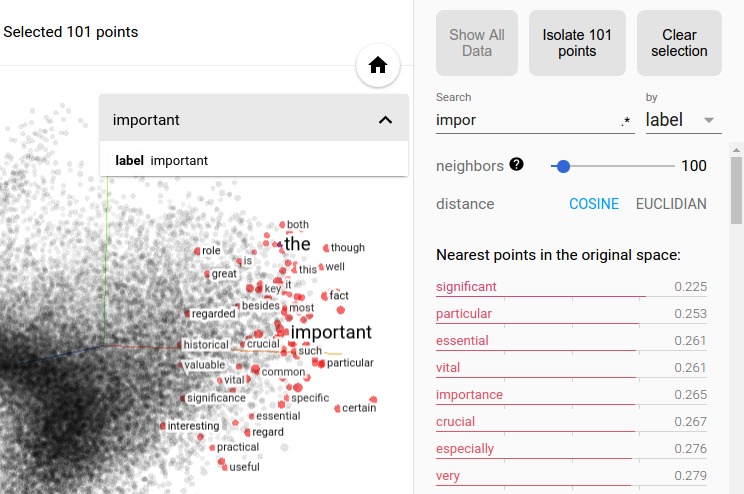
在单词Embedding数据集中选择“important”的最近邻居。
高级提示:使用自定义投影进行过滤很强大,下面,我们过滤了“politics”的100个最近邻居,并将它们投影到“worst” – “best”向量上作为x轴。 y轴是随机的。因此,您可以在右侧找到“ideas”,“science”,“perspective”,“journalism”,但在左侧找到“crisis”,“violence”和“conflict”。
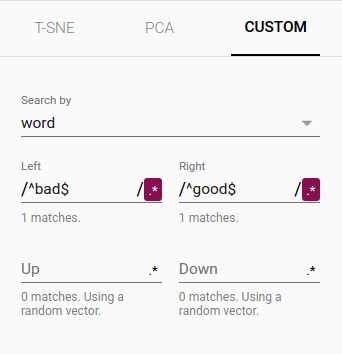
|

|
| 自定义投影控件。 | 将”politics”的邻居自定义投影到”best” – “worst”向量上。 |
要共享您的发现,您可以使用右下角的书签面板,并将当前状态(包括任何投影的计算坐标)保存为小文件。然后可以将投影指向一组一个或多个这些文件,制作下面的面板。然后其他用户可以通过一系列书签浏览。
Metadata(元数据)
如果您正在使用Embedding,则可能需要将标签/图像附加到数据点。您可以通过生成包含每个点的标签的元数据文件并在Embedding投影的数据面板中单击”Load data”来完成此操作。
元数据可以是标签或图像,它们存储在单独的文件中。对于标签,格式应该是aTSV文件(以红色显示的制表符),其第一行包含列标题(以粗体显示),后续行包含元数据值。例如:
Word\tFrequency
Airplane\t345
Car\t241
...
除标题外,假定元数据文件中行的顺序与嵌入变量中的向量的顺序相匹配。因此,元数据文件中的第(i + 1)行对应于Embedding变量的i-th行。如果TSV元数据文件只有一个列,那么我们不希望有一个标题行,并假设每一行都是嵌入的标签。我们兼容这个异常,因为它与通用的”vocab file”格式相匹配。
要将图像用作元数据,您必须生成一个精灵图像,由小缩略图组成,Embedding中的每个矢量一个。精灵应该以row-first顺序存储缩略图:第一个数据点放置在左上方,最后一个数据点放在右下方,尽管最后一行不需要填充,如下所示。
参考这个链接:在Embedding投影中查看缩略图的有趣示例。
Mini-FAQ
“embedding”是动作还是事物?都是。人们讨论在矢量空间(行为)中Embedding单词,以及在生成单词Embedding(事物)。两者共同的是Embedding作为从离散对象到矢量的映射的概念。创建或应用该映射是一个操作,但映射本身是一个事物。
Embedding成high-dimensional(高维)还是low-dimensional(低维)?看情况。例如,单词和短语的300维矢量空间通常被称为low-dimensional(低维和稠密),与它可以包含的数百万个单词和短语相比。但在数学上它是high-dimensional,显示出许多与我们的人类直觉了解的二维和三维空间有很大不同的属性。
Embedding是否与Embedding层相同?不是。Embedding层是神经网络的一部分,但一个Embedding是一个更一般的概念。
