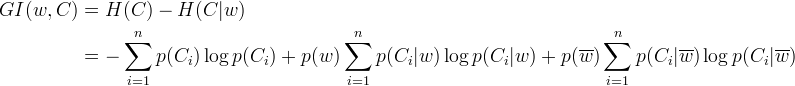在机器学习中,训练出的模型的好坏,很大程度上取决特征的选择是否恰当。例如SVM模型要取得优秀的分类效果,通常需要配合卡方选择才能实现。这是因为,大量的低质特征有时候会抹杀优质特征的区分度,要么过拟合,要么欠拟合,降低了模型的准确率和召回率。特别是特征维度很高的情况下,特征选择显得尤为重要,常用的特征选择方法主要有:
- 频次
- 卡方
- 信息增益
- 互信息
- 期望交叉熵
下文分别予以介绍。
频次
频次这个比较简单,就是看某个特征在所有训练集中的出现次数。例如,我们有3000个训练集样本,统计发现某特征A只出现在5个样本中(无论是正例还是负例),那么特征A就是个超低频特征,对模型的预测性作用不大,可以直接踢掉。总之,我们可以统计训练集中每个特征的出现频次,将低频特征过滤掉。
卡方
卡方的英文名是chi-square distribution,也可以表示为χ2。假设我们要做文本二分类,那么卡方可以帮助我们衡量某单词w跟文档类型C是否相关,根据这个相关程度,我们就可以过滤掉无用的单词,也就是做文本分类的特征选择。以经典的“篮球” 和 “体育”是否相关为例,我么来看看卡方是如何量化衡量着个相关程度的。
| 单词\类型 | 体育类 | 非体育类 |
|---|---|---|
| 包含篮球 | A | B |
| 不包含篮球 | C | D |
如上表所示,我们对训练语料中单词在正负语料中的分布做了统计之后,得出包含“篮球”是体育类和非体育类样本的数量分别是A和B,不包含“篮球”是体育和非体育中的样本数量分别是C和D
进一步得到:
| 类型 | 值 | 概率(近似) |
|---|---|---|
| 文档总数 | N = A + B + C + D | – |
| 包含“篮球” | A + B | P1 = (A + B)/N |
| 不含“篮球” | C + D | P2 = (C + D)/N |
| 体育类 | A + C | P3 = (A + C)/N |
| 非体育类 | B + D | P4 = (B + D)/N |
假设含”篮球”和体育类不相关,那么包含“篮球”且是体育类的概率是:
P = P1 * P3= (A + B)/N * (A+C)/N,
那么包含“篮球”且是体育类的期望值:
E 1 = P * N = (A + B)/N * (A + C) /N * N = (A + B) * (A + C) / N
根据卡方检验度量误差的方法:
我们可以得到含“篮球”和体育不相关 这个假设的靠谱程度为: (A – E1)^2/E1(这个值越小,即假设的误差越小,也就是假设成立的可能性越大)。同理可以得到:
含”篮球”和非体育不相关/不含“篮球”和体育不相关/不含“篮球”和非体育不相关这三个假设的靠谱程度。综上,我们可以得到四个假设,将这四个假设的靠谱程度求和,即可以得到篮球和体育不相关的所有假设的靠谱程度:
其中E1/E2/E3/E4分别是A/B/C/D对应的期望值。结合上面的X值和E值,我们做化简运算得到:
χ2(篮球, 体育)=
这个就是卡方的公式(二分类情形),这个值越大,假设也就越不成立,也就是说篮球和体育越相关。所以我们可以通过卡方值来判断特征是否和类型相关:卡方越大越相关,特征需要保留;卡方越小越不相关,特征需要过滤掉。通常,我们做特征选择时,会保留卡方值最大的K个特征,也就是说使用到的是卡方的相对值(做比较),所以公式中的N(样本总数)在实践中可以去掉。
信息增益
说到信息增益,不得不说一下信息量和信息熵的概念。如果某事件χi已经发生,那么它含有的信息量为:
如果事件χi未发生,那么I(χi)表示事件的不确定性。熵的本质是用来度量系统的不确定性的,不确定性越大,熵越高。它被定义为一个系统中所有事件的平均信息量,也可以认为是变量不确定度的期望。假设一个系统S只由一个变量X组成(X取值是χ1, χ2, χ3 …,χn,出现的概率依次为p(χ1), p(χ2), p(χ3) …,p(χn)),那么信息熵就可以用来度量S的信息量,变量的值越不确定,信息熵越高(S信息量越大)。信息熵一般公式为(对数log以2为底):
我们把这个概念迁移到文本分类上面来理解,还是以“篮球”和体育类的关系为例(这里使用具体的数值)。
| 单词\类型 | 体育类 | 非体育类 | 合计 |
|---|---|---|---|
| 包含篮球 | 100 | 20 | 120 |
| 不包含篮球 | 50 | 30 | 80 |
| 合计 | 150 | 50 | 200 |
在不知道语料中“篮球”这个词分布的情况下,我们只知道这个分类问题中体育类和非体育类的统计量,其信息熵为:
H1 = -(p[体育]* log(p[体育]) + p[非体育] * log(p[非体育])
= -(150/200 * log(150/200) + 50/200 * log(50/200)) = 0.8113
当“篮球”特征加入之后,信息熵就变成了语料中“篮球“出现和不出现这两个确定的条件下的熵之和。
H2 = -(p[含“篮球”] * (H(体育|含“篮球”))+ p[不含”篮球”] (H(体育|不含“篮球”) )
= -(120/200 * ( 100/120 * log(100/120) + 20/120 * log(20/120)) + 80/200 * (50/80 * log(50/80) + 30/80 * log(30/80))) = 0.7714
信息增益GI = H1 – H2 = 0.8113 – 0.7714 = 0.0399,这个增量值反映的是加入某个特征之后,整个分类系统的收益,增益越大,对分类效果的作用越大。那么,就可以通过信息增益来判断特征对分类系统的贡献程度,增益大的特征倾向于保留,增益小的特征倾向于剔除。这就是基于信息增益的特征选择。信息增益的一般公式如下:
———————————————————————公式(2)
信息增益除用在特征选择之外,还可以用于连续特征离散化(特征分段),以及决策树的节点选择。
互信息
互信息用来度量两个变量的相关性,互信息越大变量越相关,互信息为0时,变量互相独立。在文本分类这个例子中,w和C是离散型变量,单词w与某类别Ci的互信息一般定义为:
其中,p(w|Ci)是Ci类文档中单词w出现的概率,p(w)是单词w出现的概率。在文本分类系统中,词条w跟类C的互信息为:
这个公式也叫平均互信息。当:
MI(w, C) 远小于0, 表示w和C不相关[负相关];
MI(w, C) 远大于0, 表示w和C强相关[正相关];
MI(w, C) 约等于0, 表示w和C弱相关。
篮球和体育的问题是二分类,所以这里取N=2,C1和C2分别是体育类和非体育类,那么可以得到:
MI(篮球, 体育)= 150/200 * log((100/150)/(120/200)) + 50/200 * log((20/50)/(120/200)) = -0.0322。
注意,单词在不同的类别上的互信息有正有负,也就是说可能跟某些类别强相关,跟另外的类别弱相关,那么就可能存在正负抵消的问题,所以实际使用中,可以使用绝对值互信息来做特征选择。绝对值互信息是将公式(3)∑后面的每一项求绝对值之后再求和。
期望交叉熵
还是以文本分类问题为例,期望望交叉熵的公式是:
期望交叉熵反映的是:文本类别C的概率分布跟限定了出现单词w之后的文本类别C的概率分布的差距。期望交叉熵越大,对文本分类结果的影响越大,所以可以使用期望交叉熵来进行特征选择,保留熵大的特征,剔除熵小的特征。
参考:
[1] http://www.cnblogs.com/zhangchaoyan
[2] http://zh.wikipedia.org/zh/%E4%BA%92%E4%BF%A1%E6%81%AF
[3] http://www.douban.com/note/205995605/
[4] http://wenku.baidu.com/link?url=aBz8SmnlC1hZDYEvI6Su8Scy1_DzNh65mGwqafcXF8KQTWJ90noONJJwmccuDI9XapPWdyuCO1_scNtFSoKvvvW9GT9wpkNY6BzFDXKBC6S
[5] http://wenku.baidu.com/view/7cea98748e9951e79b89279e.html