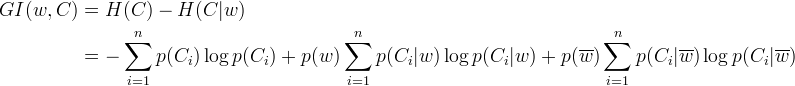在機器學習中,訓練出的模型的好壞,很大程度上取決特征的選擇是否恰當。例如SVM模型要取得優秀的分類效果,通常需要配合卡方選擇才能實現。這是因為,大量的低質特征有時候會抹殺優質特征的區分度,要麽過擬合,要麽欠擬合,降低了模型的準確率和召回率。特別是特征維度很高的情況下,特征選擇顯得尤為重要,常用的特征選擇方法主要有:
- 頻次
- 卡方
- 信息增益
- 互信息
- 期望交叉熵
下文分別予以介紹。
頻次
頻次這個比較簡單,就是看某個特征在所有訓練集中的出現次數。例如,我們有3000個訓練集樣本,統計發現某特征A隻出現在5個樣本中(無論是正例還是負例),那麽特征A就是個超低頻特征,對模型的預測性作用不大,可以直接踢掉。總之,我們可以統計訓練集中每個特征的出現頻次,將低頻特征過濾掉。
卡方
卡方的英文名是chi-square distribution,也可以表示為χ2。假設我們要做文本二分類,那麽卡方可以幫助我們衡量某單詞w跟文檔類型C是否相關,根據這個相關程度,我們就可以過濾掉無用的單詞,也就是做文本分類的特征選擇。以經典的“籃球” 和 “體育”是否相關為例,我麽來看看卡方是如何量化衡量著個相關程度的。
| 單詞\類型 | 體育類 | 非體育類 |
|---|---|---|
| 包含籃球 | A | B |
| 不包含籃球 | C | D |
如上表所示,我們對訓練語料中單詞在正負語料中的分布做了統計之後,得出包含“籃球”是體育類和非體育類樣本的數量分別是A和B,不包含“籃球”是體育和非體育中的樣本數量分別是C和D
進一步得到:
| 類型 | 值 | 概率(近似) |
|---|---|---|
| 文檔總數 | N = A + B + C + D | – |
| 包含“籃球” | A + B | P1 = (A + B)/N |
| 不含“籃球” | C + D | P2 = (C + D)/N |
| 體育類 | A + C | P3 = (A + C)/N |
| 非體育類 | B + D | P4 = (B + D)/N |
假設含”籃球”和體育類不相關,那麽包含“籃球”且是體育類的概率是:
P = P1 * P3= (A + B)/N * (A+C)/N,
那麽包含“籃球”且是體育類的期望值:
E 1 = P * N = (A + B)/N * (A + C) /N * N = (A + B) * (A + C) / N
根據卡方檢驗度量誤差的方法:
我們可以得到含“籃球”和體育不相關 這個假設的靠譜程度為: (A – E1)^2/E1(這個值越小,即假設的誤差越小,也就是假設成立的可能性越大)。同理可以得到:
含”籃球”和非體育不相關/不含“籃球”和體育不相關/不含“籃球”和非體育不相關這三個假設的靠譜程度。綜上,我們可以得到四個假設,將這四個假設的靠譜程度求和,即可以得到籃球和體育不相關的所有假設的靠譜程度:
其中E1/E2/E3/E4分別是A/B/C/D對應的期望值。結合上麵的X值和E值,我們做化簡運算得到:
χ2(籃球, 體育)=
這個就是卡方的公式(二分類情形),這個值越大,假設也就越不成立,也就是說籃球和體育越相關。所以我們可以通過卡方值來判斷特征是否和類型相關:卡方越大越相關,特征需要保留;卡方越小越不相關,特征需要過濾掉。通常,我們做特征選擇時,會保留卡方值最大的K個特征,也就是說使用到的是卡方的相對值(做比較),所以公式中的N(樣本總數)在實踐中可以去掉。
信息增益
說到信息增益,不得不說一下信息量和信息熵的概念。如果某事件χi已經發生,那麽它含有的信息量為:
如果事件χi未發生,那麽I(χi)表示事件的不確定性。熵的本質是用來度量係統的不確定性的,不確定性越大,熵越高。它被定義為一個係統中所有事件的平均信息量,也可以認為是變量不確定度的期望。假設一個係統S隻由一個變量X組成(X取值是χ1, χ2, χ3 …,χn,出現的概率依次為p(χ1), p(χ2), p(χ3) …,p(χn)),那麽信息熵就可以用來度量S的信息量,變量的值越不確定,信息熵越高(S信息量越大)。信息熵一般公式為(對數log以2為底):
我們把這個概念遷移到文本分類上麵來理解,還是以“籃球”和體育類的關係為例(這裏使用具體的數值)。
| 單詞\類型 | 體育類 | 非體育類 | 合計 |
|---|---|---|---|
| 包含籃球 | 100 | 20 | 120 |
| 不包含籃球 | 50 | 30 | 80 |
| 合計 | 150 | 50 | 200 |
在不知道語料中“籃球”這個詞分布的情況下,我們隻知道這個分類問題中體育類和非體育類的統計量,其信息熵為:
H1 = -(p[體育]* log(p[體育]) + p[非體育] * log(p[非體育])
= -(150/200 * log(150/200) + 50/200 * log(50/200)) = 0.8113
當“籃球”特征加入之後,信息熵就變成了語料中“籃球“出現和不出現這兩個確定的條件下的熵之和。
H2 = -(p[含“籃球”] * (H(體育|含“籃球”))+ p[不含”籃球”] (H(體育|不含“籃球”) )
= -(120/200 * ( 100/120 * log(100/120) + 20/120 * log(20/120)) + 80/200 * (50/80 * log(50/80) + 30/80 * log(30/80))) = 0.7714
信息增益GI = H1 – H2 = 0.8113 – 0.7714 = 0.0399,這個增量值反映的是加入某個特征之後,整個分類係統的收益,增益越大,對分類效果的作用越大。那麽,就可以通過信息增益來判斷特征對分類係統的貢獻程度,增益大的特征傾向於保留,增益小的特征傾向於剔除。這就是基於信息增益的特征選擇。信息增益的一般公式如下:
———————————————————————公式(2)
信息增益除用在特征選擇之外,還可以用於連續特征離散化(特征分段),以及決策樹的節點選擇。
互信息
互信息用來度量兩個變量的相關性,互信息越大變量越相關,互信息為0時,變量互相獨立。在文本分類這個例子中,w和C是離散型變量,單詞w與某類別Ci的互信息一般定義為:
其中,p(w|Ci)是Ci類文檔中單詞w出現的概率,p(w)是單詞w出現的概率。在文本分類係統中,詞條w跟類C的互信息為:
這個公式也叫平均互信息。當:
MI(w, C) 遠小於0, 表示w和C不相關[負相關];
MI(w, C) 遠大於0, 表示w和C強相關[正相關];
MI(w, C) 約等於0, 表示w和C弱相關。
籃球和體育的問題是二分類,所以這裏取N=2,C1和C2分別是體育類和非體育類,那麽可以得到:
MI(籃球, 體育)= 150/200 * log((100/150)/(120/200)) + 50/200 * log((20/50)/(120/200)) = -0.0322。
注意,單詞在不同的類別上的互信息有正有負,也就是說可能跟某些類別強相關,跟另外的類別弱相關,那麽就可能存在正負抵消的問題,所以實際使用中,可以使用絕對值互信息來做特征選擇。絕對值互信息是將公式(3)∑後麵的每一項求絕對值之後再求和。
期望交叉熵
還是以文本分類問題為例,期望望交叉熵的公式是:
期望交叉熵反映的是:文本類別C的概率分布跟限定了出現單詞w之後的文本類別C的概率分布的差距。期望交叉熵越大,對文本分類結果的影響越大,所以可以使用期望交叉熵來進行特征選擇,保留熵大的特征,剔除熵小的特征。
參考:
[1] http://www.cnblogs.com/zhangchaoyan
[2] http://zh.wikipedia.org/zh/%E4%BA%92%E4%BF%A1%E6%81%AF
[3] http://www.douban.com/note/205995605/
[4] http://wenku.baidu.com/link?url=aBz8SmnlC1hZDYEvI6Su8Scy1_DzNh65mGwqafcXF8KQTWJ90noONJJwmccuDI9XapPWdyuCO1_scNtFSoKvvvW9GT9wpkNY6BzFDXKBC6S
[5] http://wenku.baidu.com/view/7cea98748e9951e79b89279e.html