我正在構建一個回歸模型,我需要計算下麵的內容來檢查相關性
-
2個多級分類(類別)變量之間的相關性
-
多級分類變量與連續變量之間的相關性
-
多級分類變量的VIF(方差膨脹因子)
我認為在上述場景中使用Pearson相關係數是錯誤的,因為Pearson僅適用於2個連續變量。
請回答以下問題
-
哪種相關係數最適合上述情況?
-
VIF計算僅適用於連續數據,那麽替代方案是什麽?
-
在使用您建議的相關係數之前,我需要檢查哪些假設是否滿足?
-
如何用SAS& R中實現。
最佳解決方案
兩個類別變量
檢查兩個分類變量是否獨立可以通過卡方(Chi-Squared)獨立性測試完成。
典型的卡方檢驗Chi-Square test:如果我們假設兩個變量是獨立的,那麽這些變量的列聯表的值應該均勻分布。然後我們檢查實際值與均勻度的距離。
還可以參考這裏Crammer’s V,它是該測試的相關度量
例子
假設我們有兩個變量
-
性別:男性和女性
-
城市:Blois 和 Tours
我們觀察到了以下數據:
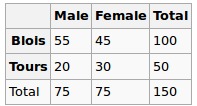
性別和城市是否獨立?我們來執行Chi-Squred測試。空假設:它們是獨立的,備選假設是它們在某種程度上是相關的。
在Null假設下,我們假設均勻分布。所以我們的預期值如下
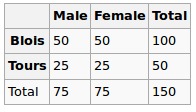
因此,我們運行chi-squared測試,這裏得到的p-value可以看作是這兩個變量之間相關性的度量。
為了計算Crammer的V,我們首先找到歸一化因子chi-squared-max,它通常是樣本的大小,將chi-square除以它並取平方根
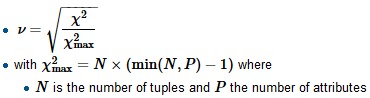
R
tbl = matrix(data=c(55, 45, 20, 30), nrow=2, ncol=2, byrow=T)
dimnames(tbl) = list(City=c('B', 'T'), Gender=c('M', 'F'))
chi2 = chisq.test(tbl, correct=F)
c(chi2$statistic, chi2$p.value)
這裏p值為0.08 – 非常小,但仍然不足以拒絕獨立假設。所以我們可以說這裏的”correlation”是0.08
我們還計算V:
sqrt(chi2$statistic / sum(tbl))
得到0.14(v越小,相關性越低)
考慮另一個數據集
Gender
City M F
B 51 49
T 24 26
為此,它將給出以下內容
tbl = matrix(data=c(51, 49, 24, 26), nrow=2, ncol=2, byrow=T)
dimnames(tbl) = list(City=c('B', 'T'), Gender=c('M', 'F'))
chi2 = chisq.test(tbl, correct=F)
c(chi2$statistic, chi2$p.value)
sqrt(chi2$statistic / sum(tbl))
p-value是0.72,它更接近1,v是0.03 – 非常接近0
類別與數值變量
對於這種類型,我們通常執行One-way ANOVA test:我們計算類內in-group方差和類間intra-group方差,然後比較它們。
例子
我們想要研究甜甜圈吸收脂肪與用於生產甜甜圈的脂肪類型之間的關係(例子來自here)
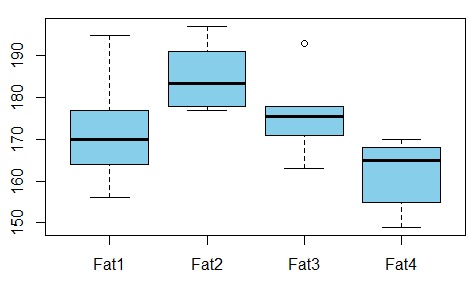
變量之間是否存在依賴關係?為此,我們進行ANOVA測試,發現p-value僅為0.007 – 這些變量之間沒有相關性。
R
t1 = c(164, 172, 168, 177, 156, 195)
t2 = c(178, 191, 197, 182, 185, 177)
t3 = c(175, 193, 178, 171, 163, 176)
t4 = c(155, 166, 149, 164, 170, 168)
val = c(t1, t2, t3, t4)
fac = gl(n=4, k=6, labels=c('type1', 'type2', 'type3', 'type4'))
aov1 = aov(val ~ fac)
summary(aov1)
輸出是
Df Sum Sq Mean Sq F value Pr(>F)
fac 3 1636 545.5 5.406 0.00688 **
Residuals 20 2018 100.9
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
因此,我們也可以將p-value作為相關度量。
