我正在构建一个回归模型,我需要计算下面的内容来检查相关性
-
2个多级分类(类别)变量之间的相关性
-
多级分类变量与连续变量之间的相关性
-
多级分类变量的VIF(方差膨胀因子)
我认为在上述场景中使用Pearson相关系数是错误的,因为Pearson仅适用于2个连续变量。
请回答以下问题
-
哪种相关系数最适合上述情况?
-
VIF计算仅适用于连续数据,那么替代方案是什么?
-
在使用您建议的相关系数之前,我需要检查哪些假设是否满足?
-
如何用SAS& R中实现。
最佳解决方案
两个类别变量
检查两个分类变量是否独立可以通过卡方(Chi-Squared)独立性测试完成。
典型的卡方检验Chi-Square test:如果我们假设两个变量是独立的,那么这些变量的列联表的值应该均匀分布。然后我们检查实际值与均匀度的距离。
还可以参考这里Crammer’s V,它是该测试的相关度量
例子
假设我们有两个变量
-
性别:男性和女性
-
城市:Blois 和 Tours
我们观察到了以下数据:
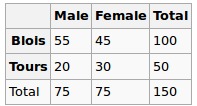
性别和城市是否独立?我们来执行Chi-Squred测试。空假设:它们是独立的,备选假设是它们在某种程度上是相关的。
在Null假设下,我们假设均匀分布。所以我们的预期值如下
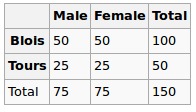
因此,我们运行chi-squared测试,这里得到的p-value可以看作是这两个变量之间相关性的度量。
为了计算Crammer的V,我们首先找到归一化因子chi-squared-max,它通常是样本的大小,将chi-square除以它并取平方根
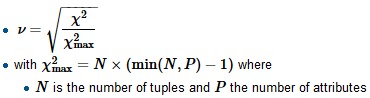
R
tbl = matrix(data=c(55, 45, 20, 30), nrow=2, ncol=2, byrow=T)
dimnames(tbl) = list(City=c('B', 'T'), Gender=c('M', 'F'))
chi2 = chisq.test(tbl, correct=F)
c(chi2$statistic, chi2$p.value)
这里p值为0.08 – 非常小,但仍然不足以拒绝独立假设。所以我们可以说这里的”correlation”是0.08
我们还计算V:
sqrt(chi2$statistic / sum(tbl))
得到0.14(v越小,相关性越低)
考虑另一个数据集
Gender
City M F
B 51 49
T 24 26
为此,它将给出以下内容
tbl = matrix(data=c(51, 49, 24, 26), nrow=2, ncol=2, byrow=T)
dimnames(tbl) = list(City=c('B', 'T'), Gender=c('M', 'F'))
chi2 = chisq.test(tbl, correct=F)
c(chi2$statistic, chi2$p.value)
sqrt(chi2$statistic / sum(tbl))
p-value是0.72,它更接近1,v是0.03 – 非常接近0
类别与数值变量
对于这种类型,我们通常执行One-way ANOVA test:我们计算类内in-group方差和类间intra-group方差,然后比较它们。
例子
我们想要研究甜甜圈吸收脂肪与用于生产甜甜圈的脂肪类型之间的关系(例子来自here)
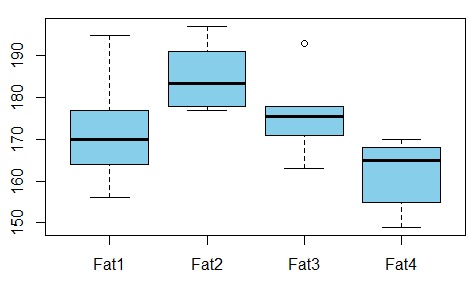
变量之间是否存在依赖关系?为此,我们进行ANOVA测试,发现p-value仅为0.007 – 这些变量之间没有相关性。
R
t1 = c(164, 172, 168, 177, 156, 195)
t2 = c(178, 191, 197, 182, 185, 177)
t3 = c(175, 193, 178, 171, 163, 176)
t4 = c(155, 166, 149, 164, 170, 168)
val = c(t1, t2, t3, t4)
fac = gl(n=4, k=6, labels=c('type1', 'type2', 'type3', 'type4'))
aov1 = aov(val ~ fac)
summary(aov1)
输出是
Df Sum Sq Mean Sq F value Pr(>F)
fac 3 1636 545.5 5.406 0.00688 **
Residuals 20 2018 100.9
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
因此,我们也可以将p-value作为相关度量。
