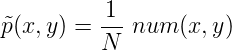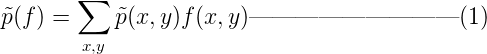這篇文章是結合論文http://www.cqvip.com/Main/Detail.aspx?id=7707219對博文：http://www.cnblogs.com/hexinuaa/p/3353479.html加入自己的理解做了簡化重寫，另外本文末尾附上了最大熵模型的實現。
一個例子 我們通過一個簡單的例子來了解最大熵的概念。假設現在需要做一個自動將英語到法語的翻譯模型，為了方便說明，我們將這個問題簡化為將英文句子中的單詞{in}翻譯成法語詞匯。那麽翻譯模型p就是對於給定包含單詞”in”的英文句子，需要給出選擇某個法語單詞f 做為”in”的翻譯結果的概率p(f)。為了幫助開發這個模型，需要收集大量已經翻譯好的樣本數據。收集好樣本之後，接下來需要做兩件事情：一是從樣本中抽取規則（特征），二是基於這些規則建立模型。
從樣本中我們能得到的第一個規則就是in可能被翻譯成的法語詞匯有：
{dans, en, à, au cours de, pendant}。
也就是說，我們可以給模型p施加第一個約束條件：
p(dans)+p(en)+ p(à)+p(au cours de)+p(pendant) = 1。
這個等式是翻譯模型可以用到的第一個對樣本的統計信息。顯然，有無數可以滿足上麵約束的模型p可供選擇，例如：
p(dans)=1，即這個模型總是預測dans
或者
p(pendant)=1/2 and p(à)=1/2，即模型要麽選擇預測pendant，要麽預測à。
這兩個模型都隻是在沒有足夠經驗數據的情況下，做的大膽假設。事實上我們隻知道當前可能的選項是5個法語詞匯，沒法確定究竟哪個概率分布式正確。那麽，一個更合理的模型假設可能是：
p(dans) = 1/5
p(en) = 1/5
p(à) = 1/5
p(au cours de) = 1/5
p(pendant) = 1/5
即該模型將概率均等地分給5個詞匯。但現實情況下，肯定不會這麽簡單，所以我們嘗試收集更多的經驗知識。假設我們從語料中發現有30%的情況下，in會被翻譯成dans 或者en，那麽運用這個知識來更新我們的模型，得到2模型約束：
p(dans) + p(en) = 3/10
p(dans)+p(en)+ p(à)+p(au cours de)+p(pendant) = 1
同樣，還是有很多概率分布滿足這兩個約束。在沒有其他知識的情況下，最直觀的模型p應該是最均勻的模型（例如，我拿出一個色子問你丟出5的概率是多少，你肯定會回答1/6），也就是在滿足約束條件的情況下，將概率均等分配：
p(dans) = 3/20
p(en) = 3/20
p(à) = 7/30
p(au cours de) = 7/30
p(pendant) = 7/30
假設我們再一次觀察樣本數據，發現：有一半的情況，in被翻譯成了dans 或 à。這樣，我們有就了3個模型約束：
p(dans) + p(en) = 3/10
p(dans)+p(en)+ p(à)+p(au cours de)+p(pendant) = 1
p(dans)+ p(à)=1/2
我們可以再一次選擇滿足3個約束的最均勻的模型p，但這一次結果沒有那麽明顯。由於經驗知識的增加，問題的複雜度也增加了，歸結起來，我們要解決兩組問題：第一，均勻(uniform)究竟是什麽意思?我們怎樣度量一個模型的均勻度(uniformity)？第二，有了上述兩個問題的答案，我們如何找到滿足所有約束並且均勻的模型？
最大熵算法可以回答上麵的2組問題。直觀上來將，很簡單，即：對已知的知識建模，對未知的知識不做任何假設。換句話說，在給定一組事實（features + output）的情況下，選擇符合所有事實，且在其他方麵盡可能均勻的模型。這也是我們在上麵的例子中，每次選擇最恰當的模型用到的原理。俗話說，不把雞蛋放在一個籃子裏，正是運用的這個原理來規避風險。
最大熵(MaxEnt)建模
我們考察一個隨機過程，它的輸出是y, y屬於有窮集合Y。對於上麵提到的例子，該過程輸出”in”的翻譯結果y， y∈Y = {dans, en, à, au cours de, pendant}。在輸出y時，該過程會受到”in”在句子中上下文信息x的影響, x屬於有窮集合X。在上文的例子中，這個x主要就是在英文句子中”in”周圍的單詞。
我們的任務就是構造一個統計模型，該模型的任務是：在給定上下文x的情況下，輸出y的概率p(y|x)。
訓練數據
為了研究上述過程，我們觀察一段時間隨機過程的行為，收集到大量的樣本數據：（x1, y1), (x2, y2), …, (xN, yN)。在之前討論的例子中，每個樣本包括：在英文句子中”in”周圍的單詞x，”in”的翻譯y。假設我們已經拿到了足夠多的訓練樣本，我們可以用樣本的經驗分布p~來表示所有樣本的分布特性：
其中N為訓練樣本的大小, num(x,y)是樣本中某一對(x,y)同時出現的次數。
特征和約束
我們的目標是構造一個能產生訓練樣本這一隨機過程p~(x,y)的統計模型。而我們能夠使用的數據就是對訓練樣本的各種統計信息或者說特征。定義特征如下：
這個也叫指示函數(indicator function)，它表示某個特定的x和某個特定的y之間是否有一定的關係。例如，在之前的例子中，如果April這個詞出現在in之後，那麽in會被翻譯成en，那麽這個特征可以表示成：
特征f(x,y)關於訓練樣本經驗分布p~(x,y)的期望如下，這個是我們可以在語料中統計到的特征經驗值：
而特征關於模型分布p(y|x)的理論期望值是：
其中p~(x)是x在訓練樣本中的經驗分布。我們約束這一期望值和訓練樣本中的經驗值相等：即要求期望概率值等於經驗概率值。
結合等式(1)(2)(3)我們得到等式：
我們稱等式(3)為約束(constraint)。我們隻關注滿足約束(3)的模型p(y|x)，也就是說不再考察跟訓練樣本的特征經驗值不一致的模型。
到這裏，我們已經有辦法來表示訓練樣本中內在的統計現象（p~(f)），同時也有辦法來讓模型擬合這一現象(p(f) = p~(f))。
最大熵原理
再回到之前例子中的問題：什麽是均勻?
數學上，條件分布p(y|x)的均勻度就是條件熵，定義如下：
熵的最小值是0，這時模型沒有任何不確定性；熵的最大值是log|Y|, 即在所有可能的y(|Y|個)上的均勻分布。
有了這個條件熵，最大熵的原理定義為：當從允許的概率分布集合C中選擇一個模型時，選擇模型p*∈C ，使得熵H(p)最大。即：
其中C的含義是所有滿足約束的模型集合，n為特征或者說特征函數fi的數量（注意跟樣本數量N區別)。
指數形式
最大熵要解決的是約束優化問題：find the p*∈C which maximizes H(p)。對於上述翻譯的例子，如果隻施加了前麵兩個約束，很容易直接求得p的分布。但是，絕大多數情況下最大熵模模型的解無法直接給出，我們需要引入像拉格朗日乘子（Lagrange Multiplier）這樣的方法。
我們具體要優化的問題是：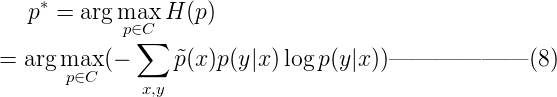 
相應的約束為： 
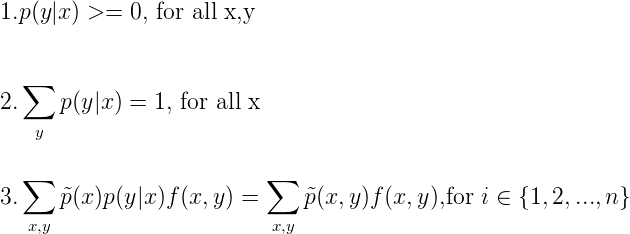為解決這個優化問題，為每一個fi引入參數λi ，得到拉格朗日函數ζ(p, Λ, γ)如下： 
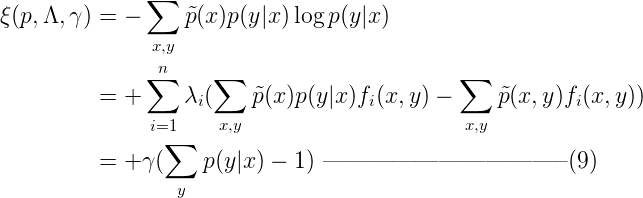其中實值參數Λ = {λ1, λ2, …, λn}和γ對應著約束2和3的n+1個限製。保持Λ和γ不變，計算拉格朗日函數ζ(p, Λ, γ)在不受限的情況下的最大值，即可得到p(y|x)的最優解。因此對ζ(p, Λ, γ)在p(y|x)上求導得（注意為了方便計算，我們這裏對數以自然對數e為底）： 
令上式（10）等於0，即：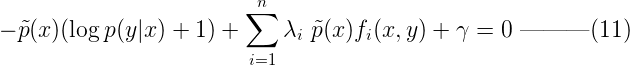 
解上麵的單變量方程(把p(y|x)當未知數)，可得p(y|x) ： 
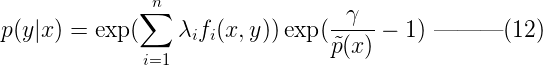根據約束2，對於任意x, Σyp(y|x) = 1，我們對等式(12)兩邊分別求和，可以得到： 
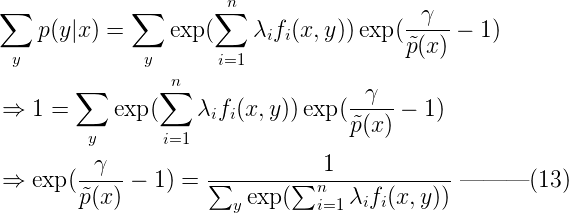將等式(13)代入等式（12），可以得到： 
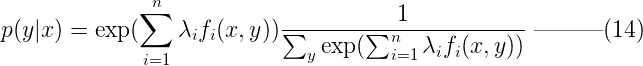令Z(x) 為： 
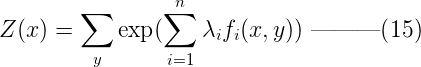則模型p(y|x)的最優解為，其中Z(x)稱為歸一化因子: 
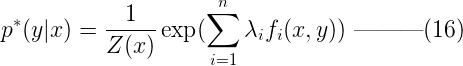到這裏，我們可以看到，滿足約束C的最大熵模型具有（16）的參數化形式。由於拉格朗日函數ζ(p, Λ, γ)中的p(y|x)和γ都可以表示成Λ，所以接下來的問題就轉化成了求解參數Λ = {λ1, λ2, …, λn}。為此，我們定義對偶函數ψ( Λ ) 及其優化問題： 
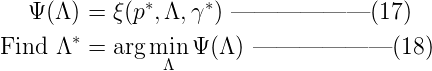根據所謂的Kuhn-Tucker theorem(KTT)原理（這個目前還沒研究，暫不展開），我們有如下結論：公式（16）中模型p*(y|x)中的參數Λ，可以通過最小化對偶函數ψ( Λ ) 求解，如(17)(18)所示。 計算參數 求解Λ = {λ1, λ2, …, λn}，解析的方法是行不通的。這種最大熵模型對應的最優化問題，一般有GIS/IIS，IIS是GIS的優化版。這裏討論最簡單的GIS。GIS的一般步驟是：
1. 初始化所有λi 為任意值，一般可以設置為0，即： 
其中λ的上標(t)表示第t論迭代，下標i表示第i個特征，n是特征總數。 2. 重複下麵的權值更新直至收斂：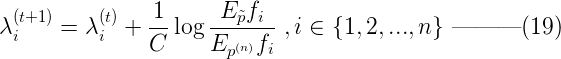 
收斂的判斷依據可以是λi 前後兩次的差價足夠小。其中C一般取所有樣本數據中最大的特征數量，Ep~和Ep如下: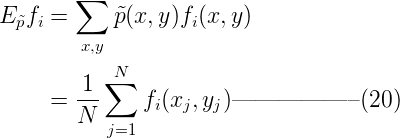 
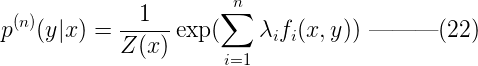代碼實現見：揭開機器學習的麵紗：最大熵模型100行代碼實現[Python版] 【轉載請注明，純淨的天空出品:https://vimsky.com/2015/05/714.html】