Python SciPy stats.vonmises_fisher用法及代碼示例

本文簡要介紹 python 語言中 scipy.stats.vonmises_fisher 的用法。

用法:

scipy.stats.vonmises_fisher = <scipy.stats._multivariate.vonmises_fisher_gen object>#

馮 Mises-Fisher 變量。

mu 關鍵字指定平均方向向量。 kappa 關鍵字指定濃度參數。

參數 ：：

mu： array_like

分布的平均方向。必須是範數為 1 的一維單位向量。

kappa： 浮點數

濃度參數。必須是正的。

seed： {無，int，np.random.RandomState，np.random.Generator}，可選

用於繪製隨機變量。如果種子是None， 這RandomState使用單例。如果種子是一個 int，一個新的RandomState使用實例，用種子播種。如果種子已經是一個RandomState或者Generator實例，然後使用該對象。默認為None.

注意：

von Mises-Fisher 分布是單位超球麵表麵上的方向分布。單位向量\(\mathbf{x}\)的概率密度函數為

\[f(\mathbf{x}) = \frac{\kappa^{d/2-1}}{(2\pi)^{d/2}I_{d/2-1}(\kappa)} \exp\left(\kappa \mathbf{\mu}^T\mathbf{x}\right),\]

其中\(\mathbf{\mu}\)是平均方向，\(\kappa\)是濃度參數，\(d\)是尺寸，\(I\)是第一類修正貝塞爾函數。由於 \(\mu\) 表示方向，因此它必須是單位向量，或者換句話說，超球麵上的點： \(\mathbf{\mu}\in S^{d-1}\) 。 \(\kappa\) 是一個濃度參數，這意味著它必須為正值 ( \(\kappa>0\) )，並且隨著 \(\kappa\) 的增加，分布變得更窄。從這個意義上說，倒數\(1/\kappa\)類似於正態分布的方差參數。

von Mises-Fisher 分布通常用作球體上正態分布的模擬。直觀上，對於單位向量，有用的距離度量由它們之間的角度\(\alpha\)給出。這正是 von Mises-Fisher 概率密度函數中的標量積 \(\mathbf{\mu}^T\mathbf{x}=\cos(\alpha)\) 所說明的：平均方向 \(\mathbf{\mu}\) 和向量 \(\mathbf{x}\) 之間的角度。它們之間的角度越大，觀察到該特定平均方向 \(\mathbf{\mu}\) 的 \(\mathbf{x}\) 的概率就越小。

在 2 維和 3 維中，使用專門的算法進行快速采樣 [2]、[3]。對於 4 或更高的維度，使用[4]中說明的拒絕采樣算法。該實現部分基於 geomstats 包 [5]、[6]。

參考：

[1]

Von Mises-Fisher 分布，維基百科，https://en.wikipedia.org/wiki/Von_Mises%E2%80%93Fisher_distribution

[2]

Mardia, K. 和 Jupp, P. 方向統計。威利，2000。

[3]

J.文澤爾. S2 上 von Mises Fisher 分布的數值穩定采樣。https://www.mitsuba-renderer.org/~wenzel/files/vmf.pdf

[4]

Wood, A. von Mises Fisher 分布的模擬。 statistics-simulation 中的通信和計算 23, 1 (1994), 157-164。 https://doi.org/10.1080/03610919408813161

[5]

地理統計器，Github。麻省理工學院許可證。訪問時間：2023 年 1 月 6 日。 https://github.com/geomstats/geomstats

[6]

米奧蘭，N.等人。 Geomstats：機器學習中黎曼幾何的 Python 包。機器學習研究雜誌 21 (2020)。 http://jmlr.org/papers/v21/19-027.html

例子：

概率密度的可視化

繪製三個維度的概率密度以增加濃度參數。密度通過pdf方法計算。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import vonmises_fisher
>>> from matplotlib.colors import Normalize
>>> n_grid = 100
>>> u = np.linspace(0, np.pi, n_grid)
>>> v = np.linspace(0, 2 * np.pi, n_grid)
>>> u_grid, v_grid = np.meshgrid(u, v)
>>> vertices = np.stack([np.cos(v_grid) * np.sin(u_grid),
...                      np.sin(v_grid) * np.sin(u_grid),
...                      np.cos(u_grid)],
...                     axis=2)
>>> x = np.outer(np.cos(v), np.sin(u))
>>> y = np.outer(np.sin(v), np.sin(u))
>>> z = np.outer(np.ones_like(u), np.cos(u))
>>> def plot_vmf_density(ax, x, y, z, vertices, mu, kappa):
...     vmf = vonmises_fisher(mu, kappa)
...     pdf_values = vmf.pdf(vertices)
...     pdfnorm = Normalize(vmin=pdf_values.min(), vmax=pdf_values.max())
...     ax.plot_surface(x, y, z, rstride=1, cstride=1,
...                     facecolors=plt.cm.viridis(pdfnorm(pdf_values)),
...                     linewidth=0)
...     ax.set_aspect('equal')
...     ax.view_init(azim=-130, elev=0)
...     ax.axis('off')
...     ax.set_title(rf"$\kappa={kappa}$")
>>> fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(9, 4),
...                          subplot_kw={"projection": "3d"})
>>> left, middle, right = axes
>>> mu = np.array([-np.sqrt(0.5), -np.sqrt(0.5), 0])
>>> plot_vmf_density(left, x, y, z, vertices, mu, 5)
>>> plot_vmf_density(middle, x, y, z, vertices, mu, 20)
>>> plot_vmf_density(right, x, y, z, vertices, mu, 100)
>>> plt.subplots_adjust(top=1, bottom=0.0, left=0.0, right=1.0, wspace=0.)
>>> plt.show()

當我們增加集中參數時，點在平均方向周圍變得更加聚集。

采樣

使用 rvs 方法從分布中抽取 5 個樣本，生成 5x3 數組。

>>> rng = np.random.default_rng()
>>> mu = np.array([0, 0, 1])
>>> samples = vonmises_fisher(mu, 20).rvs(5, random_state=rng)
>>> samples
array([[ 0.3884594 , -0.32482588,  0.86231516],
       [ 0.00611366, -0.09878289,  0.99509023],
       [-0.04154772, -0.01637135,  0.99900239],
       [-0.14613735,  0.12553507,  0.98126695],
       [-0.04429884, -0.23474054,  0.97104814]])

這些樣本是球體 \(S^2\) 上的單位向量。為了驗證，讓我們計算它們的歐幾裏得範數：

>>> np.linalg.norm(samples, axis=1)
array([1., 1., 1., 1., 1.])

繪製從 von Mises-Fisher 分布中繪製的 20 個觀測值，以增加濃度參數 \(\kappa\) 。紅點突出顯示平均方向 \(\mu\) 。

>>> def plot_vmf_samples(ax, x, y, z, mu, kappa):
...     vmf = vonmises_fisher(mu, kappa)
...     samples = vmf.rvs(20)
...     ax.plot_surface(x, y, z, rstride=1, cstride=1, linewidth=0,
...                     alpha=0.2)
...     ax.scatter(samples[:, 0], samples[:, 1], samples[:, 2], c='k', s=5)
...     ax.scatter(mu[0], mu[1], mu[2], c='r', s=30)
...     ax.set_aspect('equal')
...     ax.view_init(azim=-130, elev=0)
...     ax.axis('off')
...     ax.set_title(rf"$\kappa={kappa}$")
>>> mu = np.array([-np.sqrt(0.5), -np.sqrt(0.5), 0])
>>> fig, axes = plt.subplots(nrows=1, ncols=3,
...                          subplot_kw={"projection": "3d"},
...                          figsize=(9, 4))
>>> left, middle, right = axes
>>> plot_vmf_samples(left, x, y, z, mu, 5)
>>> plot_vmf_samples(middle, x, y, z, mu, 20)
>>> plot_vmf_samples(right, x, y, z, mu, 100)
>>> plt.subplots_adjust(top=1, bottom=0.0, left=0.0,
...                     right=1.0, wspace=0.)
>>> plt.show()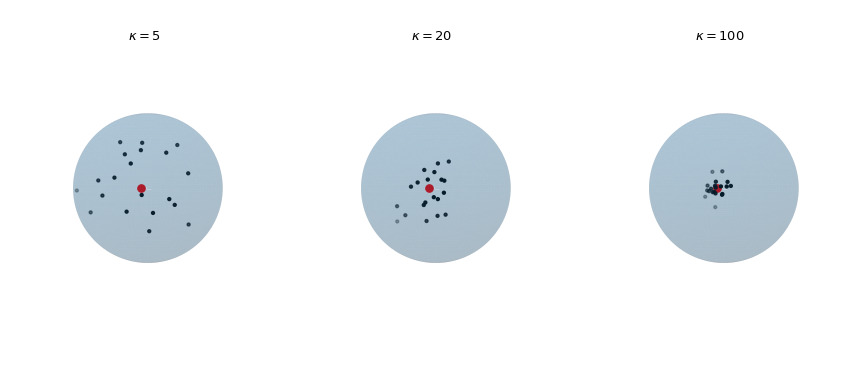

該圖顯示，隨著濃度 \(\kappa\) 的增加，所得樣本更加集中在平均方向周圍。

擬合分布參數

可以使用返回估計參數的 fit 方法將分布擬合到數據。作為一個玩具示例，讓我們將分布擬合到從已知 von Mises-Fisher 分布中抽取的樣本。

>>> mu, kappa = np.array([0, 0, 1]), 20
>>> samples = vonmises_fisher(mu, kappa).rvs(1000, random_state=rng)
>>> mu_fit, kappa_fit = vonmises_fisher.fit(samples)
>>> mu_fit, kappa_fit
(array([0.01126519, 0.01044501, 0.99988199]), 19.306398751730995)

我們看到估計的參數mu_fit和kappa_fit非常接近地麵實況參數。