本文簡要介紹 python 語言中 scipy.stats.ecdf 的用法。
用法:
scipy.stats.ecdf(sample)#樣本的經驗累積分布函數。
經驗累積分布函數 (ECDF) 是樣本基礎分布 CDF 的階躍函數估計。該函數返回代表經驗分布函數及其補充函數(經驗生存函數)的對象。
- sample: 一維數組或
scipy.stats.CensoredData 除了 數組 之外,還支持包含未經審查的
scipy.stats.CensoredData和 right-censored 觀察值的實例。目前,scipy.stats.CensoredData的其他實例將生成NotImplementedError。
- sample: 一維數組或
- res:
ECDFResult 具有以下屬性的對象。
- cdf
EmpiricalDistributionFunction 表示經驗累積分布函數的對象。
- 順豐
EmpiricalDistributionFunction 代表經驗生存函數的對象。
cdf 和 sf 屬性本身具有以下屬性。
- 分位數 ndarray
樣本中定義經驗 CDF/SF 的唯一值。
- 概率 ndarray
與分位數對應的概率的點估計。
以及以下方法:
- 評估(x):
評估參數處的 CDF/SF。
- 繪圖(軸):
在提供的軸上繪製 CDF/SF。
- confidence_interval(confidence_level=0.95):
計算分位數值處 CDF/SF 周圍的置信區間。
- cdf
- res:
參數 ::
返回 ::
注意:
當樣本的每次觀測都是精確測量時,ECDF 在每次觀測時都會增加
1/len(sample)[1]。當觀測值是下限、上限或同時是上限和下限時,數據被稱為“censored”,並且樣本可以作為一個實例提供
scipy.stats.CensoredData.對於right-censored數據,ECDF由Kaplan-Meier估計器給出[2];目前不支持其他形式的審查。
置信區間根據 Greenwood 公式或更新的 “Exponential Greenwood” 公式計算,如 [4] 中所述。
參考:
[1] (1,2,3)康諾弗,威廉·傑伊。實用非參數統計。卷。 350. 約翰·威利父子公司,1999。
[2]卡普蘭、愛德華·L.和保羅·邁爾。 “來自不完整觀察的非參數估計。”美國統計協會雜誌 53.282 (1958): 457-481。
[3]戈埃爾、曼尼什·庫馬爾、帕迪普·卡納和朱加爾·基肖爾。 “了解生存分析:Kaplan-Meier 估計。”國際阿育吠陀研究雜誌 1.4(2010):274。
[4]索耶、斯坦利. “生存分析中的格林伍德和指數格林伍德置信區間。”https://www.math.wustl.edu/~sawyer/handouts/greenwood.pdf
例子:
未經審查的數據
正如第 79 頁 [1] 中的示例一樣,從一所高中的學生中隨機選擇了 5 個男孩。他們的one-mile運行時間記錄如下。
>>> sample = [6.23, 5.58, 7.06, 6.42, 5.20] # one-mile run times (minutes)經驗分布函數近似於對男孩進行抽樣的總體 one-mile 運行時間的分布函數,計算如下。
>>> from scipy import stats >>> res = stats.ecdf(sample) >>> res.cdf.quantiles array([5.2 , 5.58, 6.23, 6.42, 7.06]) >>> res.cdf.probabilities array([0.2, 0.4, 0.6, 0.8, 1. ])將結果繪製為階躍函數:
>>> import matplotlib.pyplot as plt >>> ax = plt.subplot() >>> res.cdf.plot(ax) >>> ax.set_xlabel('One-Mile Run Time (minutes)') >>> ax.set_ylabel('Empirical CDF') >>> plt.show()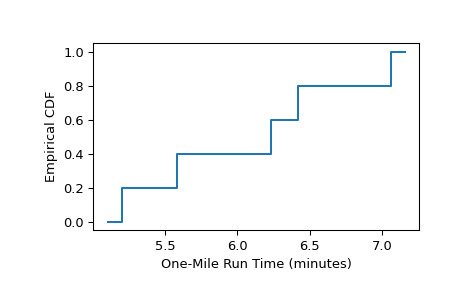
Right-censored數據
正如第 91 頁 [1] 中的示例一樣,測試了 10 個汽車風扇皮帶的壽命。五項測試因所測試的風扇皮帶斷裂而結束,但其餘測試因其他原因而結束(例如,該研究耗盡了資金,但風扇皮帶仍然有效)。使用風扇皮帶行駛的裏程記錄如下。
>>> broken = [77, 47, 81, 56, 80] # in thousands of miles driven >>> unbroken = [62, 60, 43, 71, 37]測試結束時仍能發揮作用的風扇皮帶的準確生存時間尚不清楚,但已知它們超過了
unbroken中記錄的值。因此,這些觀測值被稱為 “right-censored”,並且數據使用scipy.stats.CensoredData表示。>>> sample = stats.CensoredData(uncensored=broken, right=unbroken)經驗生存函數計算如下。
>>> res = stats.ecdf(sample) >>> res.sf.quantiles array([37., 43., 47., 56., 60., 62., 71., 77., 80., 81.]) >>> res.sf.probabilities array([1. , 1. , 0.875, 0.75 , 0.75 , 0.75 , 0.75 , 0.5 , 0.25 , 0. ])將結果繪製為階躍函數:
>>> ax = plt.subplot() >>> res.cdf.plot(ax) >>> ax.set_xlabel('Fanbelt Survival Time (thousands of miles)') >>> ax.set_ylabel('Empirical SF') >>> plt.show()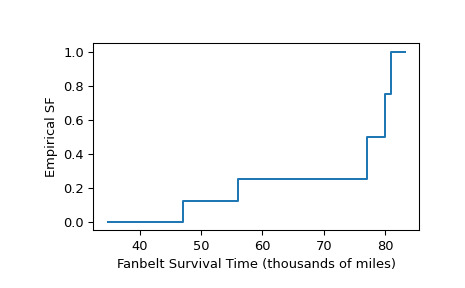
相關用法
- Python SciPy stats.exponpow用法及代碼示例
- Python SciPy stats.expon用法及代碼示例
- Python SciPy stats.expectile用法及代碼示例
- Python SciPy stats.entropy用法及代碼示例
- Python SciPy stats.exponnorm用法及代碼示例
- Python SciPy stats.energy_distance用法及代碼示例
- Python SciPy stats.exponweib用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
- Python SciPy stats.iqr用法及代碼示例
- Python SciPy stats.genpareto用法及代碼示例
- Python SciPy stats.skewnorm用法及代碼示例
- Python SciPy stats.cosine用法及代碼示例
- Python SciPy stats.norminvgauss用法及代碼示例
- Python SciPy stats.directional_stats用法及代碼示例
- Python SciPy stats.invwishart用法及代碼示例
- Python SciPy stats.bartlett用法及代碼示例
- Python SciPy stats.levy_stable用法及代碼示例
- Python SciPy stats.page_trend_test用法及代碼示例
- Python SciPy stats.itemfreq用法及代碼示例
- Python SciPy stats.gumbel_l用法及代碼示例
- Python SciPy stats.chisquare用法及代碼示例
- Python SciPy stats.semicircular用法及代碼示例
- Python SciPy stats.gzscore用法及代碼示例
- Python SciPy stats.gompertz用法及代碼示例
- Python SciPy stats.normaltest用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.stats.ecdf。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
