本文簡要介紹 python 語言中 scipy.cluster.vq.kmeans2 的用法。
用法:
scipy.cluster.vq.kmeans2(data, k, iter=10, thresh=1e-05, minit='random', missing='warn', check_finite=True, *, seed=None)#使用 k-means 算法將一組觀測值分類為 k 個集群。
該算法試圖最小化觀測值和質心之間的歐幾裏得距離。包括幾個初始化方法。
- data: ndarray
“N”維中“M”個觀測值的“M”乘“N”個數組或“M”個一維觀測值的長度“M”個數組。
- k: int 或 ndarray
要形成的簇數以及要生成的質心數。如果 minit 初始化字符串是 ‘matrix’,或者如果給出了 ndarray,則將其解釋為要使用的初始集群。
- iter: 整數,可選
要運行的k-means 算法的迭代次數。請注意,從 iters 參數到 kmeans 函數的含義不同。
- thresh: 浮點數,可選
(尚未使用)
- minit: str,可選
初始化方法。可用的方法是‘random’, ‘points’、‘++’和‘matrix’:
‘random’:從高斯生成 k 個質心,並根據數據估計均值和方差。
‘points’:從初始質心的數據中隨機選擇 k 個觀測值(行)。
‘++’:根據 kmeans++ 方法選擇 k 個觀測值(小心播種)
‘matrix’:將 k 參數解釋為初始質心數組的 k × M(或一維數據的長度 k 數組)數組。
- missing: str,可選
處理空簇的方法。可用的方法有‘warn’和‘raise’:
‘warn’:發出警告並繼續。
‘raise’:引發ClusterError並終止算法。
- check_finite: 布爾型,可選
是否檢查輸入矩陣是否僅包含有限數。禁用可能會提高性能,但如果輸入確實包含無窮大或 NaN,則可能會導致問題(崩潰、非終止)。默認值:真
- seed: {無,int,
numpy.random.Generator,numpy.random.RandomState},可選 用於初始化偽隨機數生成器的種子。如果種子是無(或
numpy.random), 這numpy.random.RandomState使用單例。如果種子是一個 int,一個新的RandomState使用實例,播種種子.如果種子已經是一個Generator或者RandomState實例然後使用該實例。默認值為無。
- centroid: ndarray
在 k-means 的最後一次迭代中發現的由“N”個質心數組組成的 ‘k’。
- label: ndarray
label[i] 是第 i 個觀測值最接近的質心的代碼或索引。
參數 ::
返回 ::
參考:
[1]D. Arthur 和 S. Vassilvitskii,“k-means++:仔細播種的優勢”,第十八屆年度ACM-SIAM 離散算法研討會論文集,2007 年。
例子:
>>> from scipy.cluster.vq import kmeans2 >>> import matplotlib.pyplot as plt >>> import numpy as np創建 z,一個形狀為 (100, 2) 的數組,其中包含來自三個多元正態分布的樣本的混合。
>>> rng = np.random.default_rng() >>> a = rng.multivariate_normal([0, 6], [[2, 1], [1, 1.5]], size=45) >>> b = rng.multivariate_normal([2, 0], [[1, -1], [-1, 3]], size=30) >>> c = rng.multivariate_normal([6, 4], [[5, 0], [0, 1.2]], size=25) >>> z = np.concatenate((a, b, c)) >>> rng.shuffle(z)計算三個集群。
>>> centroid, label = kmeans2(z, 3, minit='points') >>> centroid array([[ 2.22274463, -0.61666946], # may vary [ 0.54069047, 5.86541444], [ 6.73846769, 4.01991898]])每個集群有多少個點?
>>> counts = np.bincount(label) >>> counts array([29, 51, 20]) # may vary繪製集群。
>>> w0 = z[label == 0] >>> w1 = z[label == 1] >>> w2 = z[label == 2] >>> plt.plot(w0[:, 0], w0[:, 1], 'o', alpha=0.5, label='cluster 0') >>> plt.plot(w1[:, 0], w1[:, 1], 'd', alpha=0.5, label='cluster 1') >>> plt.plot(w2[:, 0], w2[:, 1], 's', alpha=0.5, label='cluster 2') >>> plt.plot(centroid[:, 0], centroid[:, 1], 'k*', label='centroids') >>> plt.axis('equal') >>> plt.legend(shadow=True) >>> plt.show()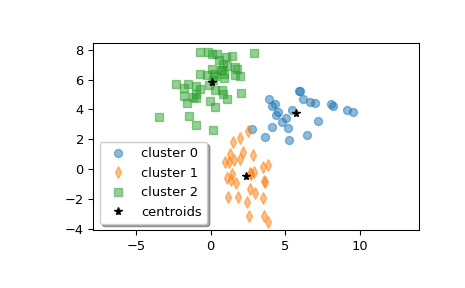
相關用法
- Python SciPy vq.kmeans用法及代碼示例
- Python SciPy vq.whiten用法及代碼示例
- Python SciPy vq.vq用法及代碼示例
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
- Python SciPy ClusterNode.pre_order用法及代碼示例
- Python SciPy stats.iqr用法及代碼示例
- Python SciPy FortranFile.read_record用法及代碼示例
- Python SciPy ndimage.correlate用法及代碼示例
- Python SciPy special.exp1用法及代碼示例
- Python SciPy special.expn用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy ndimage.morphological_gradient用法及代碼示例
- Python SciPy distance.sokalmichener用法及代碼示例
- Python SciPy linalg.eigvalsh_tridiagonal用法及代碼示例
- Python SciPy linalg.cdf2rdf用法及代碼示例
- Python SciPy csc_array.diagonal用法及代碼示例
- Python SciPy fft.idctn用法及代碼示例
- Python SciPy linalg.LaplacianNd用法及代碼示例
- Python SciPy linalg.solve_circulant用法及代碼示例
- Python SciPy hierarchy.ward用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy stats.genpareto用法及代碼示例
- Python SciPy ndimage.variance用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.cluster.vq.kmeans2。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
