Python numpy random.standard_t用法及代碼示例

本文簡要介紹 python 語言中 numpy.random.standard_t 的用法。

用法:

random.standard_t(df, size=None)

從具有 df 自由度的標準學生 t 分布中抽取樣本。

雙曲分布的一個特例。作為df變大，結果類似於標準正態分布的結果(numpy.random.standard_normal)。

注意

新代碼應改為使用default_rng() 實例的standard_t 方法；請參閱快速入門。

參數：

df： 浮點數或類似數組的浮點數

自由度，必須 > 0。

size： int 或整數元組，可選

輸出形狀。例如，如果給定的形狀是 (m, n, k) ，則繪製 m * n * k 樣本。如果 size 為 None(默認)，如果 df 是標量，則返回單個值。否則，將抽取np.array(df).size 樣本。

返回：

out： ndarray 或標量

從參數化的標準學生 t 分布中抽取樣本。

注意：

t 分布的概率密度函數為

\[P(x, df) = \frac{\Gamma(\frac{df+1}{2})}{\sqrt{\pi df} \Gamma(\frac{df}{2})}\Bigl( 1+\frac{x^2}{df} \Bigr)^{-(df+1)/2}\]

t 檢驗基於數據來自正態分布的假設。 t 檢驗提供了一種方法來測試樣本均值(即根據數據計算的均值)是否是對真實均值的良好估計。

1908 年，William Gosset 在都柏林的吉尼斯啤酒廠工作時首次發表了 t 分布的推導。由於專有問題，他不得不以化名發表，所以他使用了學生這個名字。

參考：

1：

Dalgaard, Peter，“R 的介紹性統計”，Springer，2002 年。

2：

維基百科，“學生的 t 分布”https://en.wikipedia.org/wiki/Student’s_t-distribution

例子：

從 Dalgaard 第 83 頁 [1] 中，假設 11 名女性的每日能量攝入量(以千焦耳 (kJ) 為單位)為：

>>> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515, \
...                    7515, 8230, 8770])

他們的能量攝入是否係統地偏離了 7725 kJ 的推薦值？我們的零假設將是不存在偏差，而替代假設將是存在可能是正麵或負麵的影響，因此使我們的測試成為 2 尾。

因為我們正在估計平均值並且我們的樣本中有 N=11 個值，所以我們有 N-1=10 個自由度。我們將顯著性水平設置為 95%，並使用我們攝入量的經驗平均值和經驗標準差計算 t 統計量。我們使用 1 的 ddof 將經驗標準偏差的計算基於方差的無偏估計(注意：由於平方根的凹性質，最終估計不是無偏的)。

>>> np.mean(intake)
6753.636363636364
>>> intake.std(ddof=1)
1142.1232221373727
>>> t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake)))
>>> t
-2.8207540608310198

我們從具有足夠自由度的學生 t 分布中抽取 1000000 個樣本。

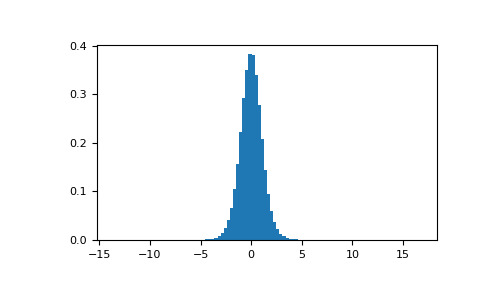
>>> import matplotlib.pyplot as plt
>>> s = np.random.standard_t(10, size=1000000)
>>> h = plt.hist(s, bins=100, density=True)

我們的 t 統計量是否落在分布兩端的兩個關鍵區域之一？

>>> np.sum(np.abs(t) < np.abs(s)) / float(len(s))
0.018318  #random < 0.05, statistic is in critical region

這個 2 尾檢驗的概率值約為 1.83%，低於 5% 的預先確定的顯著性閾值。

因此，在零假設為真的條件下觀察到像我們的攝入一樣極端的值的概率太低，我們拒絕沒有偏差的零假設。