Python numpy random.mtrand.RandomState.wald用法及代碼示例

用法： RandomState.wald(mean, scale, size=None)

從Wald或高斯逆分布中抽取樣本。

隨著尺度接近無窮大，分布變得更像高斯。一些參考文獻聲稱Wald是均值等於1的逆高斯函數，但這絕不是通用的。

高斯逆分布首先是與布朗運動有關的。 1956年Tweedie使用逆高斯這個名稱是因為覆蓋單位距離的時間與單位時間所覆蓋的距離之間存在反比關係。

參數：

參數：	mean：： float 或 array_like of floats 分布平均值，必須> 0。 scale：： float 或 array_like of floats 比例參數，必須> 0。 size：： int 或 tuple of ints, 可選參數輸出形狀。如果給定的形狀是`(m, n, k)`，然後`m * n * k`抽取樣品。如果尺寸是`None`(默認)，如果返回一個值`mean`和`scale`都是標量。除此以外，`np.broadcast(mean, scale).size`抽取樣品。
返回值：	out：： ndarray或標量從參數化的Wald分布中抽取樣本。

mean：： float 或 array_like of floats: 分布平均值，必須> 0。
scale：： float 或 array_like of floats: 比例參數，必須> 0。
size：： int 或 tuple of ints, 可選參數: 輸出形狀。如果給定的形狀是(m, n, k)，然後m * n * k抽取樣品。如果尺寸是None(默認)，如果返回一個值mean和scale都是標量。除此以外，np.broadcast(mean, scale).size抽取樣品。

返回值：

Wald分布的概率密度函數為

$P(x;mean,scale) = \sqrt{\frac{scale}{2\pi x^3}}e^ \frac{-scale(x-mean)^2}{2\cdotp mean^2x}$

如上所述，高斯逆分布首先源於對布朗運動建模的嘗試。它也是Weibull的競爭對手，可用於可靠性建模以及股票收益和利率過程的建模。

[1]	Brighton Webs Ltd.，Wald Distribution，https://web.archive.org/web/20090423014010/http://www.brighton-webs.co.uk:80/distributions/wald.asp

[2]	Chhikara，Raj S.和Folks，J。Leroy，“反高斯分布：理論：方法和應用”，CRC出版社，1988年。

[3]	維基百科，“Inverse Gaussian distribution”https://en.wikipedia.org/wiki/Inverse_Gaussian_distribution

從分布中繪製值並繪製直方圖：

>>> import matplotlib.pyplot as plt
>>> h = plt.hist(np.random.wald(3, 2, 100000), bins=200, density=True)
>>> plt.show()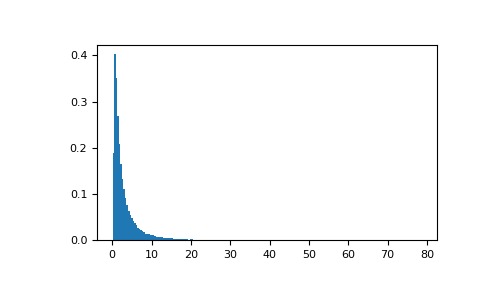

注：本文由純淨天空篩選整理自 numpy.random.mtrand.RandomState.wald。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。