Python numpy random.mtrand.RandomState.weibull用法及代碼示例

用法： RandomState.weibull(a, size=None)

從威布爾分布中抽取樣本。

從具有給定形狀參數a的1參數Weibull分布中抽取樣本。

$X = (-ln(U))^{1/a}$

在此，U是從(0,1]上的均勻分布得出的。

更為常見的2參數Weibull，包括比例參數 $\lambda$ 隻是 $X = \lambda(-ln(U))^{1/a}$ 。

參數：	a：： float 或 array_like of floats 形狀參數的分布。必須為非負數。 size：： int 或 tuple of ints, 可選參數輸出形狀。如果給定的形狀是`(m, n, k)`，然後`m * n * k`抽取樣品。如果尺寸是`None`(默認)，如果返回一個值`a`是標量。除此以外，`np.array(a).size`抽取樣品。
返回值：	out：： ndarray或標量從參數化的威布爾分布中抽取樣本。

注意：

威布爾(或最小值的類型III漸近極值分布，SEV類型III或Rosin-Rammler分布)是用於建模極值問題的一類廣義極值(GEV)分布之一。此類包括Gumbel和Frechet分布。

威布爾分布的概率密度為

$p(x) = \frac{a} {\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a},$

哪裏是形狀和 $\lambda$ 規模。

該函數的峰值(模式)為 $\lambda(\frac{a-1}{a})^{1/a}$ 。

當a = 1，威布爾分布簡化為 index 分布。

參考文獻：

[1]	Waloddi Weibull，皇家技術大學，斯德哥爾摩，1939年，“材料強度的統計理論”，Ingeniorsvetenskapsakademiens Handlingar Nr 151，1939年，斯德哥爾摩，斯德哥爾摩，Generalstabens Litografiska Anstalt。

[2]	Waloddi Weibull，“廣泛適用性的統計分布函數”，《應用力學雜誌》 ASME，1951年發表。

[3]	維基百科，“Weibull distribution”，https://en.wikipedia.org/wiki/Weibull_distribution

例子：

從分布中抽取樣本：

>>> a = 5. # shape
>>> s = np.random.weibull(a, 1000)

顯示樣本的直方圖以及概率密度函數：

>>> import matplotlib.pyplot as plt
>>> x = np.arange(1,100.)/50.
>>> def weib(x,n,a):
...     return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)

>>> count, bins, ignored = plt.hist(np.random.weibull(5.,1000))
>>> x = np.arange(1,100.)/50.
>>> scale = count.max()/weib(x, 1., 5.).max()
>>> plt.plot(x, weib(x, 1., 5.)*scale)
>>> plt.show()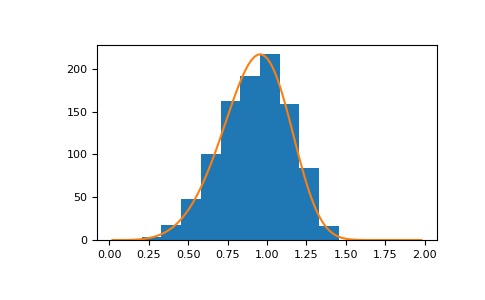

../../../_images/numpy-random-mtrand-RandomState-weibull-1.png

注：本文由純淨天空篩選整理自 numpy.random.mtrand.RandomState.weibull。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。