本文簡要介紹 python 語言中 numpy.random.pareto 的用法。
用法:
random.pareto(a, size=None)從具有指定形狀的 Pareto II 或 Lomax 分布中抽取樣本。
Lomax 或 Pareto II 分布是移動的 Pareto 分布。經典的帕累托分布可以通過加 1 並乘以尺度參數
m(見注釋)從 Lomax 分布中獲得。 Lomax 分布的最小值為零,而對於經典 Pareto 分布,它是mu,其中標準 Pareto 分布的位置為mu = 1。 Lomax 也可以被認為是廣義帕累托分布(在 SciPy 中可用)的簡化版本,比例設置為 1,位置設置為零。帕累托分布必須大於零,並且在上麵是無界的。它也被稱為“80-20 法則”。在此分布中,80% 的權重位於範圍的最低 20% 範圍內,而其他 20% 的權重填充範圍的剩餘 80%。
注意
新代碼應改為使用
default_rng()實例的pareto方法;請參閱快速入門。- a: 浮點數或類似數組的浮點數
分布的形狀。必須是正的。
- size: int 或整數元組,可選
輸出形狀。例如,如果給定的形狀是
(m, n, k),則繪製m * n * k樣本。如果 size 為None(默認),如果a是標量,則返回單個值。否則,將抽取np.array(a).size樣本。
- out: ndarray 或標量
從參數化的帕累托分布中抽取樣本。
參數:
返回:
注意:
帕累托分布的概率密度是
其中 是形狀, 是比例。
帕累托分布以意大利經濟學家維爾弗雷多·帕累托的名字命名,是一種冪律概率分布,可用於許多現實世界的問題。在經濟學領域之外,它通常被稱為布拉德福德分布。帕累托發展了分配來說明經濟中的財富分配。它還用於保險、網頁訪問統計、油田規模和許多其他問題,包括 Sourceforge 中項目的下載頻率 [1]。它是所謂的 “fat-tailed” 發行版之一。
參考:
Francis Hunt 和 Paul Johnson,關於 Sourceforge 項目的帕累托分布。
帕累托五世 (1896)。政治經濟學課程。洛桑。
Reiss, R.D., Thomas, M.(2001),極值的統計分析,Birkhauser Verlag,巴塞爾,第 23-30 頁。
維基百科,“Pareto distribution”,https://en.wikipedia.org/wiki/Pareto_distribution
1:
2:
3:
4:
例子:
從分布中抽取樣本:
>>> a, m = 3., 2. # shape and mode >>> s = (np.random.pareto(a, 1000) + 1) * m顯示樣本的直方圖以及概率密度函數:
>>> import matplotlib.pyplot as plt >>> count, bins, _ = plt.hist(s, 100, density=True) >>> fit = a*m**a / bins**(a+1) >>> plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='r') >>> plt.show()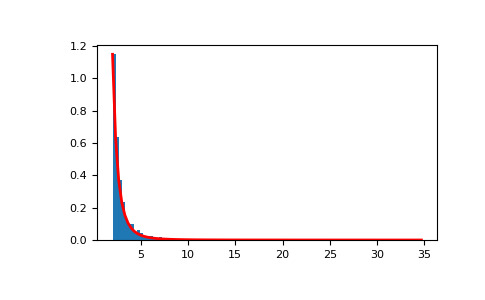
相關用法
- Python numpy random.poisson用法及代碼示例
- Python numpy random.permutation用法及代碼示例
- Python numpy random.power用法及代碼示例
- Python numpy random.mtrand.RandomState.wald用法及代碼示例
- Python numpy random.mtrand.RandomState.multivariate_normal用法及代碼示例
- Python numpy random.standard_exponential用法及代碼示例
- Python numpy random.mtrand.RandomState.gumbel用法及代碼示例
- Python numpy random.mtrand.RandomState.multinomial用法及代碼示例
- Python numpy random.rand用法及代碼示例
- Python numpy random.mtrand.RandomState.logistic用法及代碼示例
- Python numpy random.mtrand.RandomState.shuffle用法及代碼示例
- Python numpy random.triangular用法及代碼示例
- Python numpy random.noncentral_f用法及代碼示例
- Python numpy random.mtrand.RandomState.poisson用法及代碼示例
- Python numpy random.lognormal用法及代碼示例
- Python numpy random.mtrand.RandomState.seed用法及代碼示例
- Python numpy random.mtrand.RandomState.triangular用法及代碼示例
- Python numpy random.gumbel用法及代碼示例
- Python numpy random.mtrand.RandomState.weibull用法及代碼示例
- Python numpy random.shuffle用法及代碼示例
- Python numpy random.geometric用法及代碼示例
- Python numpy random.multinomial用法及代碼示例
- Python numpy random.logseries用法及代碼示例
- Python numpy random.mtrand.RandomState.rand用法及代碼示例
- Python numpy random.mtrand.RandomState.power用法及代碼示例
注:本文由純淨天空篩選整理自numpy.org大神的英文原創作品 numpy.random.pareto。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
