Python numpy random.mtrand.RandomState.power用法及代碼示例

用法：

RandomState.power(a, size=None)

從具有正 index a-1的功率分布中以[0，1]抽取樣本。

也稱為冪函數分布。

參數：	a： ： float 或 array_like of floats 分布參數。必須為非負數。 size： ： int 或 tuple of ints, 可選參數 輸出形狀。如果給定的形狀是(m, n, k)， 然後m * n * k抽取樣品。如果尺寸是None(默認)，如果返回一個值a是標量。除此以外，np.array(a).size抽取樣品。
返回值：	out： ： ndarray或標量 從參數化功率分布中抽取樣本。
異常：	ValueError： 如果<1。

注意：

概率密度函數為

冪函數分布隻是帕累托分布的倒數。它也可能被視為Beta分布的特例。

例如，它用於建模保險索賠的over-reporting。

參考文獻：

[1]	克裏斯蒂安·克萊伯(Christian Kleiber)，塞繆爾·科茨(Samuel Kotz)，“經濟學和精算科學中的統計規模分布”，威利，2003年。

[2]	Heckert，N. A.和Filliben，James J.“ NIST手冊148：數據圖參考手冊，第2卷：讓子命令和庫函數”，美國國家標準技術研究所手冊 Series ，2003年6月。https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/powpdf.pdf

例子：

從分布中抽取樣本：

>>> a = 5. # shape
>>> samples = 1000
>>> s = np.random.power(a, samples)

顯示樣本的直方圖以及概率密度函數：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, bins=30)
>>> x = np.linspace(0, 1, 100)
>>> y = a*x**(a-1.)
>>> normed_y = samples*np.diff(bins)[0]*y
>>> plt.plot(x, normed_y)
>>> plt.show()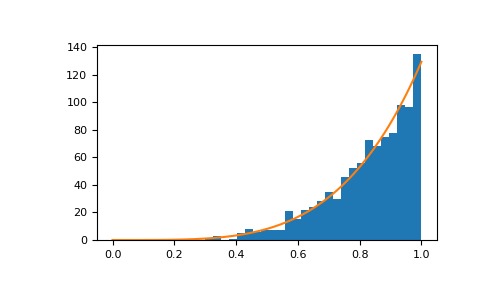

將冪函數分布與Pareto的倒數進行比較。

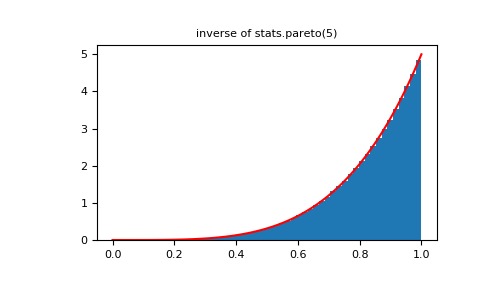
>>> from scipy import stats # doctest:+SKIP
>>> rvs = np.random.power(5, 1000000)
>>> rvsp = np.random.pareto(5, 1000000)
>>> xx = np.linspace(0,1,100)
>>> powpdf = stats.powerlaw.pdf(xx,5)  # doctest:+SKIP

>>> plt.figure()
>>> plt.hist(rvs, bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  # doctest:+SKIP
>>> plt.title('np.random.power(5)')

>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  # doctest:+SKIP
>>> plt.title('inverse of 1 + np.random.pareto(5)')

>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  # doctest:+SKIP
>>> plt.title('inverse of stats.pareto(5)')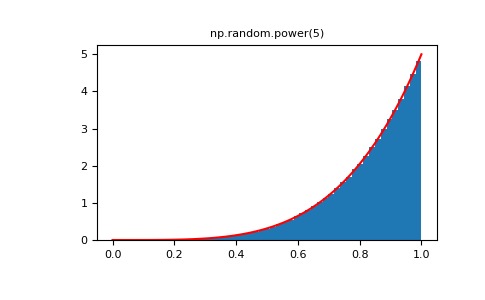

注：本文由純淨天空篩選整理自 numpy.random.mtrand.RandomState.power。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。