mean-shift聚類算法演示簡介
Mean Shift算法,又被稱為均值漂移算法。與K-Means算法一樣,都是基於聚類中心的聚類算法,不同的是, Mean Shift算法不需要事先製定類別個數k。
參考:
Dorin Comaniciu和Peter Meer,“均值變換:一種用於特征空間分析的可靠方法”。
(Dorin Comaniciu and Peter Meer, “Mean Shift: A robust approach toward feature space analysis”. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002. pp. 603-619.)
代碼實現[Python]
# -*- coding: utf-8 -*-
print(__doc__)
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs
# #############################################################################
# 生成樣本數據
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
# #############################################################################
# 使用MeanShift聚類
# The following bandwidth can be automatically detected using
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)
print("number of estimated clusters : %d" % n_clusters_)
# #############################################################################
# 繪製結果
import matplotlib.pyplot as plt
from itertools import cycle
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
my_members = labels == k
cluster_center = cluster_centers[k]
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
代碼執行
代碼運行時間大約:0分0.397秒。
運行代碼輸出的文本內容如下:
number of estimated clusters : 3
運行代碼輸出的圖片內容如下:
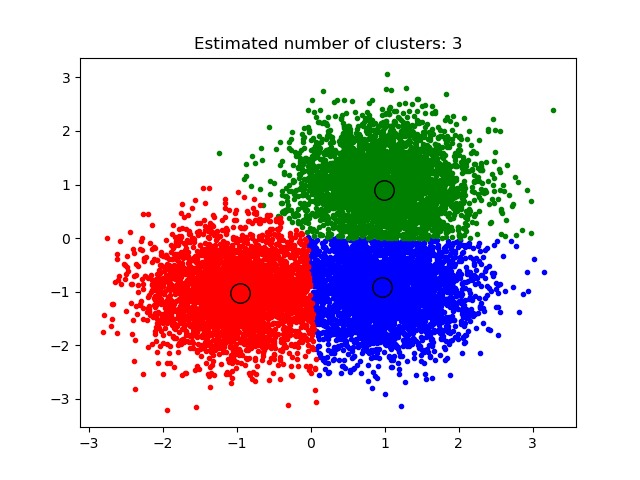
源碼下載
- Python版源碼文件: plot_mean_shift.py
- Jupyter Notebook版源碼文件: plot_mean_shift.ipynb
