当前位置: 首页>>代码示例>>用法及示例精选>>正文

python scipy cluster.hierarchy.linkage用法及代码示例

用法：

scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)

执行层次/聚集聚类。

输入y可以是1d凝聚距离矩阵或2d观测矢量数组。

如果y为一维凝聚距离矩阵，则y必须为a大小的向量，其中n是距离矩阵中配对的原始观测值的数量。该函数的行为与MATLAB链接函数非常相似。

A 4矩阵Z返回。在迭代，具有索引的聚类Z[i, 0]和Z[i, 1]合并形成集群。索引小于的集群对应于原始观察。簇之间的距离Z[i, 0]和Z[i, 1]是(谁)给的Z[i, 2]。第四个值Z[i, 3]表示新形成的群集中原始观测值的数量。

以下链接方法用于计算距离在两个集群之间和。该算法始于要在形成的层次结构中使用的群集森林。当两个集群和从这个森林中组合成一个集群，和从森林中移走，并且被添加到森林中。当林中仅剩下一个群集时，算法将停止，并且该群集将成为根。

在每次迭代中都维护一个距离矩阵。的d[i,j]条目对应于群集之间的距离和在原始森林里。

在每次迭代中，算法必须更新距离矩阵以反映新形成的群集u与森林中其余群集的距离。

假设有原始观察在集群中和原始对象在集群中。召回和合并形成集群。让是森林中任何剩余的集群。

以下是计算新形成的群集之间的距离的方法和每个。

  • method=’single’ assigns

    for all points in cluster and in cluster . This is also known as the Nearest Point Algorithm.

  • method=’complete’ assigns

    for all points in cluster u and in cluster . This is also known by the Farthest Point Algorithm or Voor Hees Algorithm.

  • method=’average’ assigns

    for all points and where and are the cardinalities of clusters and , respectively. This is also called the UPGMA algorithm.

  • method=’weighted’ assigns

    where cluster u was formed with cluster s and t and v is a remaining cluster in the forest. (also called WPGMA)

  • method=’centroid’ assigns

    where and are the centroids of clusters and , respectively. When two clusters and are combined into a new cluster , the new centroid is computed over all the original objects in clusters and . The distance then becomes the Euclidean distance between the centroid of and the centroid of a remaining cluster in the forest. This is also known as the UPGMC algorithm.

  • method=’median’ assigns like the centroid method. When two clusters and are combined into a new cluster , the average of centroids s and t give the new centroid . This is also known as the WPGMC algorithm.

  • method=’ward’ uses the Ward variance minimization algorithm. The new entry is computed as follows,

    where is the newly joined cluster consisting of clusters and , is an unused cluster in the forest, , and is the cardinality of its argument. This is also known as the incremental algorithm.

警告：选择林中的最小距离对时，可能会有两个或更多对具有相同的最小距离。此实现可以选择与MATLAB版本不同的最小值。

参数：

y：ndarray

压缩距离矩阵。压缩距离矩阵是包含距离矩阵上三角的平面阵列。这是这样的形式pdist返回。或者，收集观察向量尺寸可以作为通过数组。压缩距离矩阵的所有元素必须是有限的，即没有NaN或infs。

method：str, 可选参数

要使用的链接算法。看到Linkage Methods下面的完整说明。

metric：str 或 function, 可选参数

在y为观察向量集合的情况下使用的距离度量；否则忽略。看到pdist函数以获取有效距离度量的列表。也可以使用自定义距离函数。

optimal_ordering：bool, 可选参数

如果为True，则将对链接矩阵进行重新排序，以使连续叶子之间的距离最小。当数据可视化时，这将导致更直观的树结构。默认为False，因为此算法可能很慢，尤其是在大型数据集上[2]。另请参阅optimal_leaf_ordering函数。

1.0.0版的新函数。

返回值：

Z：ndarray

层次聚类编码为链接矩阵。

注意：

  1. 对于方法‘single’，实现了基于最小生成树的优化算法。时间复杂。对于方法‘complete’，‘average’，‘weighted’和‘ward’，实现了称为nearest-neighbors链的算法。它还具有时间复杂性。对于其他方法，可以通过以下方法实现幼稚算法：时间复杂度。所有算法使用 memory 。参考[1]有关算法的详细信息。

  2. 仅当使用欧几里德成对度量标准时，才正确定义方法‘centroid’，‘median’和‘ward’。如果将y作为预先计算的成对距离传递，则用户有责任确保这些距离实际上是欧几里得，否则产生的结果将不正确。

参考文献：

1

Daniel Mullner，“现代分层的，聚集的聚类算法”，arXiv：1109.2378v1。

2

Ziv Bar-Joseph，David K. Gifford，Tommi S. Jaakkola，“用于层次聚类的快速最佳叶排序”，2001年。DOI：10.1093 /bioinformatics /17.suppl_1.S22

例子：

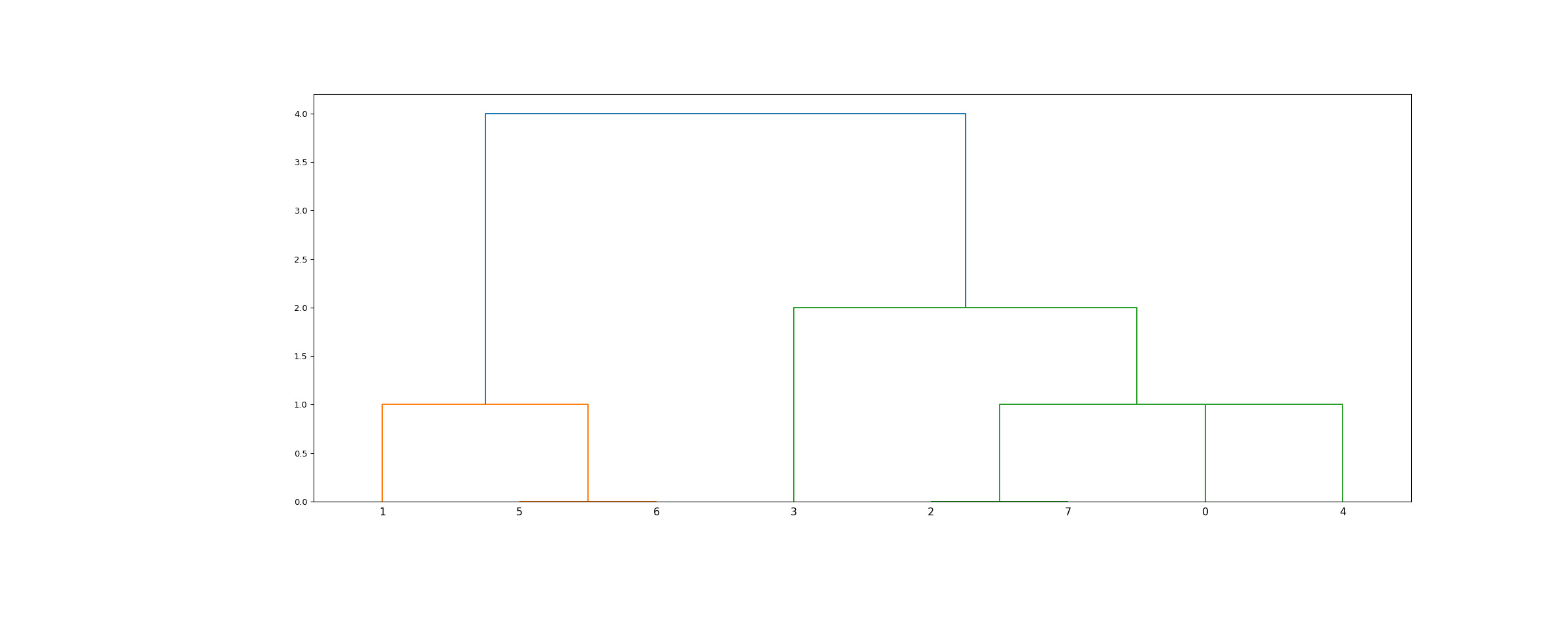
>>> from scipy.cluster.hierarchy import dendrogram, linkage
>>> from matplotlib import pyplot as plt
>>> X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]
>>> Z = linkage(X, 'ward')
>>> fig = plt.figure(figsize=(25, 10))
>>> dn = dendrogram(Z)
>>> Z = linkage(X, 'single')
>>> fig = plt.figure(figsize=(25, 10))
>>> dn = dendrogram(Z)
>>> plt.show()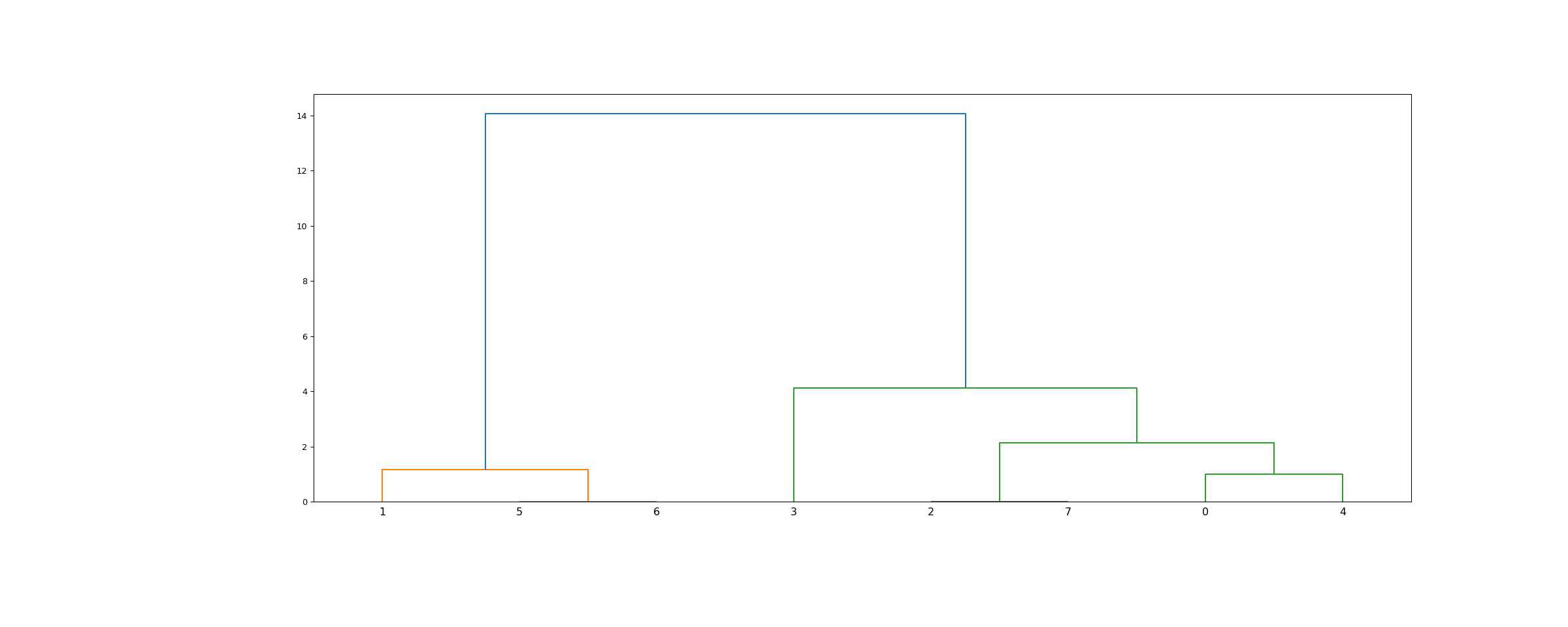
../_images/scipy-cluster-hierarchy-linkage-1_00.png
../_images/scipy-cluster-hierarchy-linkage-1_01.png

源码：

scipy.cluster.hierarchy.linkage的API实现见：[源代码]

相关用法

注：本文由纯净天空筛选整理自 scipy.cluster.hierarchy.linkage。非经特殊声明，原始代码版权归原作者所有，本译文的传播和使用请遵循“署名-相同方式共享 4.0 国际 (CC BY-SA 4.0)”协议。