分类器的概率校准简介
执行分类时,您通常不仅要预测类别标签,还要预测相关的概率。该概率使可以认为是预测结果的置信度(confidence coefficient)。但是,并非所有分类器都提供校正好的概率,其中一些是over-confident,而另一些是under-confident。
因此,通常期望对预测概率进行单独的校准作为后处理。本示例说明了两种不同的校准方法,并使用Brier分数评估了返回的概率的质量(Brier分数详细见https://en.wikipedia.org/wiki/Brier_score,简单来说,Brier分数可以被认为是对一组概率预测的“校准”的量度,或者称为“ 成本函数 ”,这一组概率对应的情况必须互斥,并且概率之和必须为1.)。
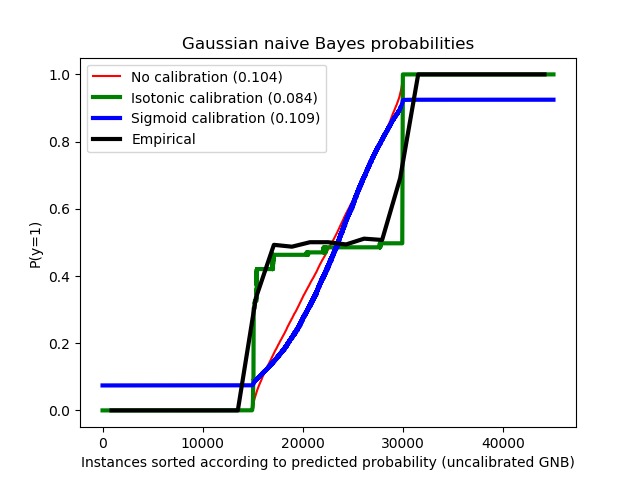
示例中使用高斯朴素贝叶斯分类器估计概率,比较了未经校准、S型校准和非参数等渗校准三种情况。可以观察到,只有非参数模型能够提供概率校准,该校准返回属于中间集群且带有异类标记的大多数样本的概率接近预期的0.5。这样可以显著提高Brier得分。
代码实现[Python]
# -*- coding: utf-8 -*-
print(__doc__)
# Author: Mathieu Blondel
# Alexandre Gramfort
# Balazs Kegl
# Jan Hendrik Metzen
# License: BSD Style.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn.datasets import make_blobs
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import brier_score_loss
from sklearn.calibration import CalibratedClassifierCV
from sklearn.model_selection import train_test_split
n_samples = 50000
n_bins = 3 # use 3 bins for calibration_curve as we have 3 clusters here
# Generate 3 blobs with 2 classes where the second blob contains
# half positive samples and half negative samples. Probability in this
# blob is therefore 0.5.
centers = [(-5, -5), (0, 0), (5, 5)]
X, y = make_blobs(n_samples=n_samples, n_features=2, cluster_std=1.0,
centers=centers, shuffle=False, random_state=42)
y[:n_samples // 2] = 0
y[n_samples // 2:] = 1
sample_weight = np.random.RandomState(42).rand(y.shape[0])
# 为校准切分训练集和测试集
X_train, X_test, y_train, y_test, sw_train, sw_test = \
train_test_split(X, y, sample_weight, test_size=0.9, random_state=42)
# 未校准的高斯朴素贝叶斯
clf = GaussianNB()
clf.fit(X_train, y_train) # GaussianNB itself does not support sample-weights
prob_pos_clf = clf.predict_proba(X_test)[:, 1]
# 使用等渗校准的高斯朴素贝叶斯
clf_isotonic = CalibratedClassifierCV(clf, cv=2, method='isotonic')
clf_isotonic.fit(X_train, y_train, sw_train)
prob_pos_isotonic = clf_isotonic.predict_proba(X_test)[:, 1]
# 使用sigmoid校准(S校准)的高斯朴素贝叶斯
clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method='sigmoid')
clf_sigmoid.fit(X_train, y_train, sw_train)
prob_pos_sigmoid = clf_sigmoid.predict_proba(X_test)[:, 1]
print("Brier scores: (the smaller the better)")
clf_score = brier_score_loss(y_test, prob_pos_clf, sw_test)
print("No calibration: %1.3f" % clf_score)
clf_isotonic_score = brier_score_loss(y_test, prob_pos_isotonic, sw_test)
print("With isotonic calibration: %1.3f" % clf_isotonic_score)
clf_sigmoid_score = brier_score_loss(y_test, prob_pos_sigmoid, sw_test)
print("With sigmoid calibration: %1.3f" % clf_sigmoid_score)
# #############################################################################
# 绘制数据和预测的概率
plt.figure()
y_unique = np.unique(y)
colors = cm.rainbow(np.linspace(0.0, 1.0, y_unique.size))
for this_y, color in zip(y_unique, colors):
this_X = X_train[y_train == this_y]
this_sw = sw_train[y_train == this_y]
plt.scatter(this_X[:, 0], this_X[:, 1], s=this_sw * 50,
c=color[np.newaxis, :],
alpha=0.5, edgecolor='k',
label="Class %s" % this_y)
plt.legend(loc="best")
plt.title("Data")
plt.figure()
order = np.lexsort((prob_pos_clf, ))
plt.plot(prob_pos_clf[order], 'r', label='No calibration (%1.3f)' % clf_score)
plt.plot(prob_pos_isotonic[order], 'g', linewidth=3,
label='Isotonic calibration (%1.3f)' % clf_isotonic_score)
plt.plot(prob_pos_sigmoid[order], 'b', linewidth=3,
label='Sigmoid calibration (%1.3f)' % clf_sigmoid_score)
plt.plot(np.linspace(0, y_test.size, 51)[1::2],
y_test[order].reshape(25, -1).mean(1),
'k', linewidth=3, label=r'Empirical')
plt.ylim([-0.05, 1.05])
plt.xlabel("Instances sorted according to predicted probability "
"(uncalibrated GNB)")
plt.ylabel("P(y=1)")
plt.legend(loc="upper left")
plt.title("Gaussian naive Bayes probabilities")
plt.show()
代码执行
代码运行时间大约:0分0.108秒。
运行代码输出的文本内容如下:
Brier scores: (the smaller the better) No calibration: 0.104 With isotonic calibration: 0.084 With sigmoid calibration: 0.109
运行代码输出的图片内容如下:
源码下载
- Python版源码文件: plot_calibration.py
- Jupyter Notebook版源码文件: plot_calibration.ipynb
