本文簡要介紹 python 語言中 scipy.signal.bessel 的用法。
用法:
scipy.signal.bessel(N, Wn, btype='low', analog=False, output='ba', norm='phase', fs=None)#Bessel/Thomson 數字和模擬濾波器設計。
設計一個Nth-order 數字或模擬貝塞爾濾波器並返回濾波器係數。
- N: int
過濾器的順序。
- Wn: array_like
給出臨界頻率(由 norm 參數定義)的標量或長度為 2 的序列。對於模擬濾波器,Wn 是角頻率(例如,rad/s)。
對於數字濾波器,Wn 的單位與 fs 相同。默認情況下,fs 為 2 half-cycles/sample,因此這些從 0 歸一化為 1,其中 1 是奈奎斯特頻率。 (因此 Wn 在 half-cycles /樣本中。)
- btype: {‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’},可選
過濾器的類型。默認為‘lowpass’。
- analog: 布爾型,可選
如果為 True,則返回模擬濾波器,否則返回數字濾波器。 (見注釋。)
- output: {‘ba’, ‘zpk’, ‘sos’},可選
輸出類型:分子/分母 (‘ba’)、pole-zero (‘zpk’) 或二階部分 (‘sos’)。默認為‘ba’。
- norm: {‘phase’, ‘delay’, ‘mag’},可選
臨界頻率歸一化:
phase濾波器被歸一化,使得相位響應在角(例如 rad/s)頻率 Wn 處達到其中點。 low-pass 和 high-pass 過濾器都會發生這種情況,因此這是 “phase-matched” 的情況。
幅度響應漸近線與截止值為 Wn 的同階巴特沃斯濾波器相同。
這是默認設置,與 MATLAB 的實現相匹配。
delay濾波器被歸一化,使得通帶中的群延遲為 1/Wn(例如,秒)。這是通過求解貝塞爾多項式得到的“natural”類型。
mag濾波器被歸一化,使得增益幅度在角頻率 Wn 處為 -3 dB。
- fs: 浮點數,可選
數字係統的采樣頻率。
- b, a: 數組,數組
分子 (b) 和分母 (a) IIR 濾波器的多項式。僅在以下情況下返回
output='ba'.- z, p, k: ndarray,ndarray,浮點數
IIR 濾波器傳遞函數的零點、極點和係統增益。僅在
output='zpk'時返回。- sos: ndarray
IIR 濾波器的二階截麵表示。僅在
output='sos'時返回。
參數 ::
返回 ::
注意:
也稱為湯姆森濾波器,模擬貝塞爾濾波器具有最大平坦群延遲和最大線性相位響應,在階躍響應中幾乎沒有振鈴。 [1]
Bessel 本質上是一個模擬濾波器。此函數使用雙線性變換生成數字貝塞爾濾波器,它不保留模擬濾波器的相位響應。因此,它僅在低於大約 fs/4 的頻率下近似正確。要在較高頻率下獲得maximally-flat 群延遲,必須使用phase-preserving 技術轉換模擬貝塞爾濾波器。
有關實現細節和參考,請參閱
besselap。'sos'輸出參數是在 0.16.0 中添加的。參考:
[1]Thomson, W.E.,“具有最大平坦頻率特性的延遲網絡”,電氣工程師學會論文集,第三部分,1949 年 11 月,卷。 96,第 44 期,第 487-490 頁。
例子:
繪製phase-normalized 頻率響應,顯示與巴特沃斯截止頻率(綠色)的關係:
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import numpy as np>>> b, a = signal.butter(4, 100, 'low', analog=True) >>> w, h = signal.freqs(b, a) >>> plt.semilogx(w, 20 * np.log10(np.abs(h)), color='silver', ls='dashed') >>> b, a = signal.bessel(4, 100, 'low', analog=True, norm='phase') >>> w, h = signal.freqs(b, a) >>> plt.semilogx(w, 20 * np.log10(np.abs(h))) >>> plt.title('Bessel filter magnitude response (with Butterworth)') >>> plt.xlabel('Frequency [radians / second]') >>> plt.ylabel('Amplitude [dB]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.axvline(100, color='green') # cutoff frequency >>> plt.show()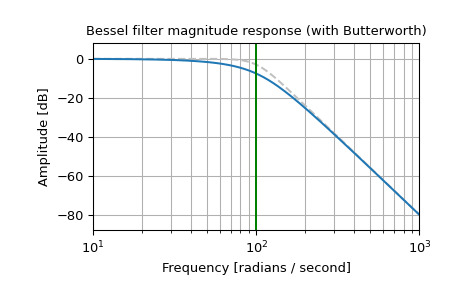
和相位中點:
>>> plt.figure() >>> plt.semilogx(w, np.unwrap(np.angle(h))) >>> plt.axvline(100, color='green') # cutoff frequency >>> plt.axhline(-np.pi, color='red') # phase midpoint >>> plt.title('Bessel filter phase response') >>> plt.xlabel('Frequency [radians / second]') >>> plt.ylabel('Phase [radians]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.show()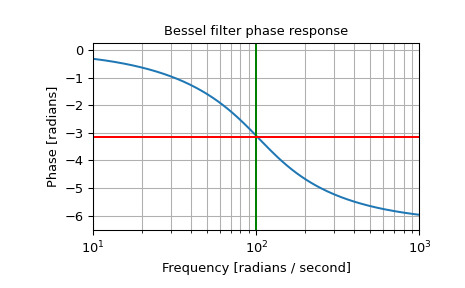
繪製 magnitude-normalized 頻率響應,顯示 -3 dB 截止:
>>> b, a = signal.bessel(3, 10, 'low', analog=True, norm='mag') >>> w, h = signal.freqs(b, a) >>> plt.semilogx(w, 20 * np.log10(np.abs(h))) >>> plt.axhline(-3, color='red') # -3 dB magnitude >>> plt.axvline(10, color='green') # cutoff frequency >>> plt.title('Magnitude-normalized Bessel filter frequency response') >>> plt.xlabel('Frequency [radians / second]') >>> plt.ylabel('Amplitude [dB]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.show()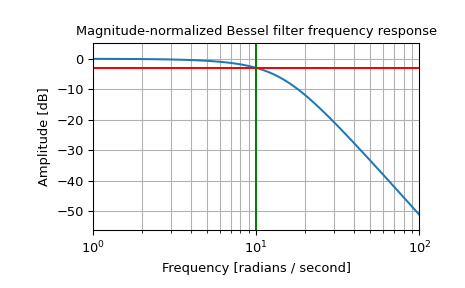
繪製 delay-normalized 濾波器,顯示 0.1 秒處的 maximally-flat 群延遲:
>>> b, a = signal.bessel(5, 1/0.1, 'low', analog=True, norm='delay') >>> w, h = signal.freqs(b, a) >>> plt.figure() >>> plt.semilogx(w[1:], -np.diff(np.unwrap(np.angle(h)))/np.diff(w)) >>> plt.axhline(0.1, color='red') # 0.1 seconds group delay >>> plt.title('Bessel filter group delay') >>> plt.xlabel('Frequency [radians / second]') >>> plt.ylabel('Group delay [seconds]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.show()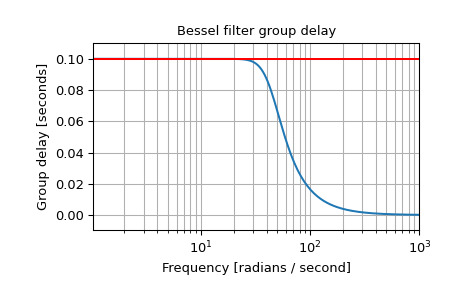
相關用法
- Python SciPy signal.bilinear_zpk用法及代碼示例
- Python SciPy signal.buttord用法及代碼示例
- Python SciPy signal.bspline用法及代碼示例
- Python SciPy signal.butter用法及代碼示例
- Python SciPy signal.bode用法及代碼示例
- Python SciPy signal.bilinear用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
- Python SciPy signal.kaiser_atten用法及代碼示例
- Python SciPy signal.oaconvolve用法及代碼示例
- Python SciPy signal.hilbert用法及代碼示例
- Python SciPy signal.ricker用法及代碼示例
- Python SciPy signal.group_delay用法及代碼示例
- Python SciPy signal.cheb2ord用法及代碼示例
- Python SciPy signal.get_window用法及代碼示例
- Python SciPy signal.lfilter用法及代碼示例
- Python SciPy signal.morlet用法及代碼示例
- Python SciPy signal.coherence用法及代碼示例
- Python SciPy signal.dfreqresp用法及代碼示例
- Python SciPy signal.TransferFunction用法及代碼示例
- Python SciPy signal.dbode用法及代碼示例
- Python SciPy signal.residuez用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.bessel。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
